РГР по физике. 1 семестр 20варик. Задача 1 вариант 20 Две материальные точки движутся согласно параметрическим уравнениям
 Скачать 293.89 Kb.
|
|
Задача №1 вариант 20 Две материальные точки движутся согласно параметрическим уравнениям:  . Найти координату, значения скорости и ускорения точек в момент времени t2. Рассчитать средние значения скоростей и ускорений в интервале времени от t2 до t3. Построить графики зависимости x(t), v(t), a(t) в интервале от t0 до t1 секунд с шагом Δt=2c. Проверить, возможна ли встреча этих материальных точек (указать по возможности на графике). Дано:
Найти:  Построить графики  Решение: Найдем координаты при t2= 22 с.   Скорость – первая производная координаты по времени, ускорение – первая производная скорости по времени.      Средние значения скоростей и ускорений в интервале времени от t2 до t3. Для этого воспользуемся уравнением среднего значения:  Найдем скорость и ускорение каждой точки в момент времени t3.       Построим графики зависимостей:  для каждой из точек в интервале времени от 17 до 27 с с шагом Δt=2c: Таблица значений для построения графиков.
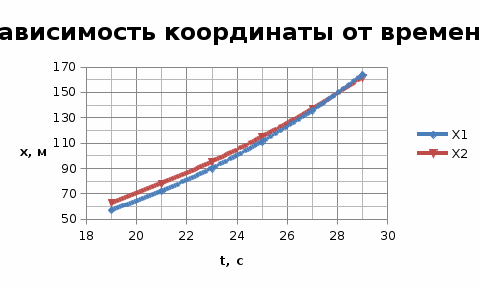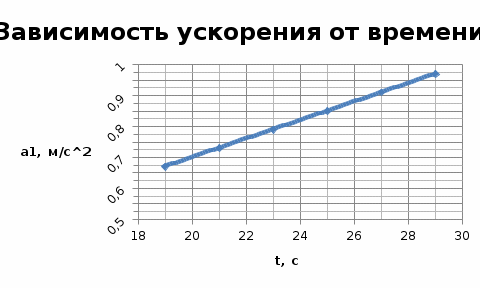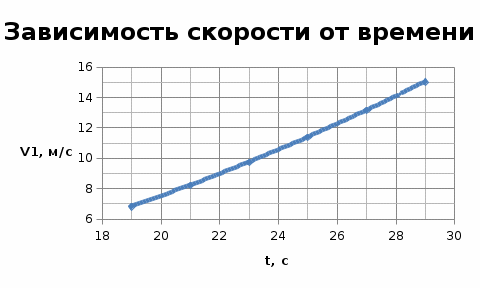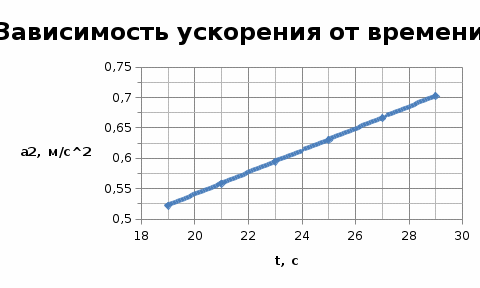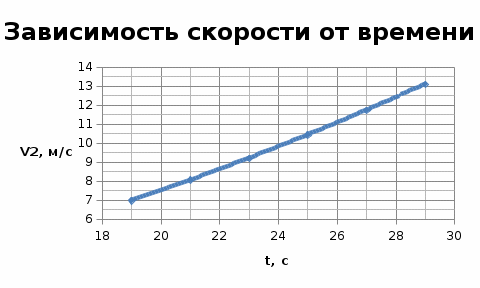     Проверим, возможна ли встреча этих материальных точек. Приравняем уравнения координат:  Подставляя числовые значения получим:   Решая данное кубическое уравнение получим точки пересечения:   Построим график движения двух точек в интервале времени от 8 до 30 с с шагом 2 с и укажем на них точки пересечения: 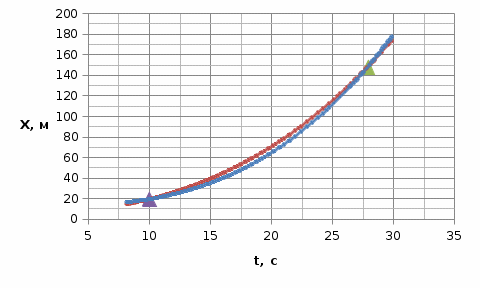 Задача №2 вариант 20. Известно, что характер движения тела вдоль горизонтаопределяется начальной высотой над нулевым уровнем и углом, под которымсообщается начальная скорость. Рассчитайте максимальную высоту подъематела над нулевым уровнем, дальность и время полета в соответствии сисходными данными. Постройте графики зависимости дальности полета имаксимальной высоты подъема при изменении угла в интервале от 40°до 85° с шагом 5°. Постройте график изменения потенциальной энергии материальной точки на всем интервале времени от t=0 до t=tn. Масштаб по оси абсцисс (по времени) выбрать таким, чтобы в данном интервале укладывалось не менее 10-ти точек. Дано: m = 2,0 кг v0 = 10,5 м/с H0 = 10,5 м α = 1050 построить графики в пределах углов 400< α <850 с шагом 50. 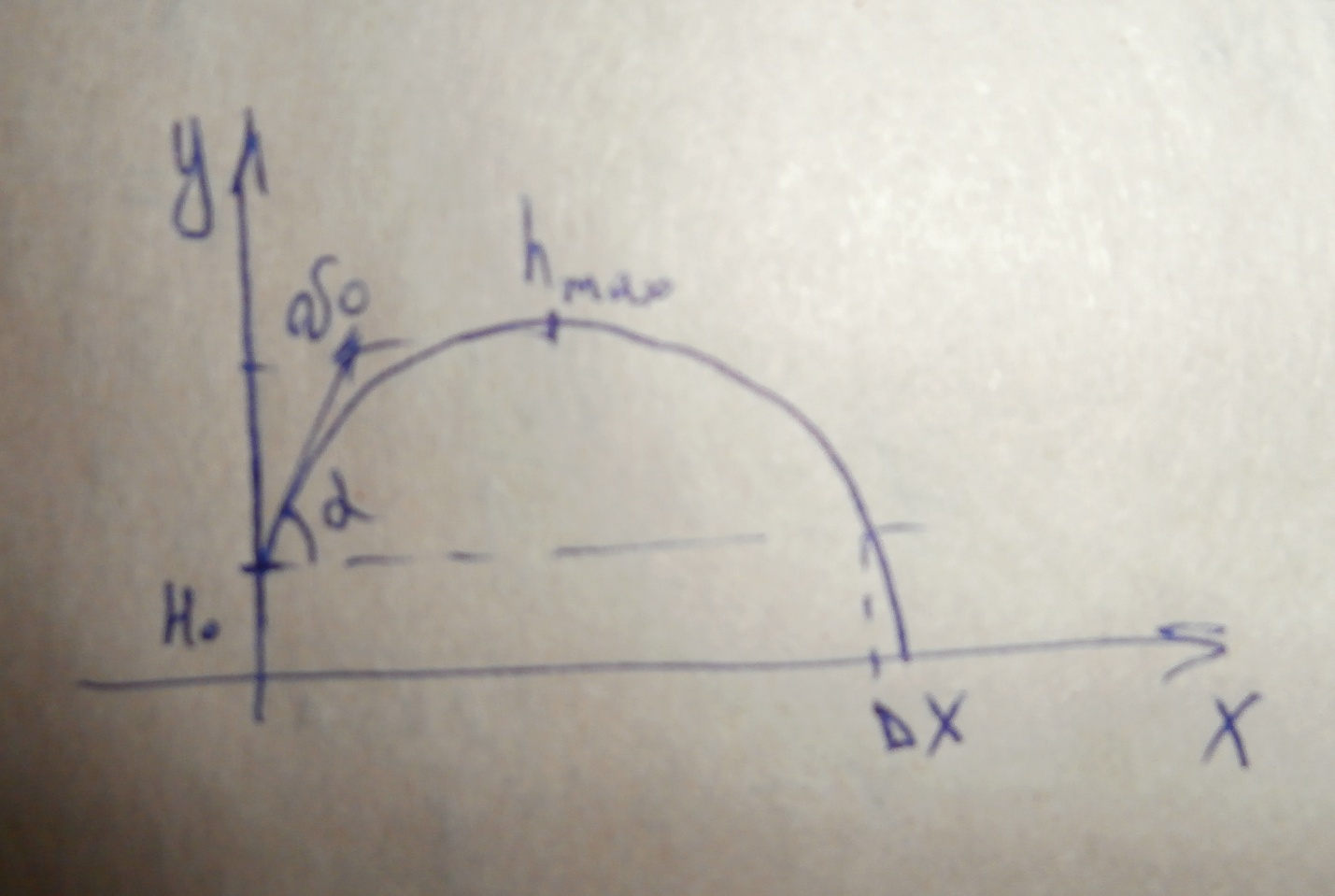 Движение материальной точки описывается двумя уравнениями: вдоль оси X и вдоль оси Y.   Максимальная высота подъема над нулевым уровнем:  Время полета найдем из уравнения движения вдоль оси X, выражая скорости подставляя получим:  Дальность полета:  Потенциальная энергия зависит от высоты: E=mgh h – расстояние по Y. Подставляем в выражение получим:  Таблица для построения графиков.
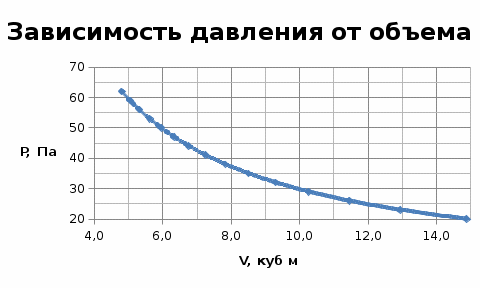
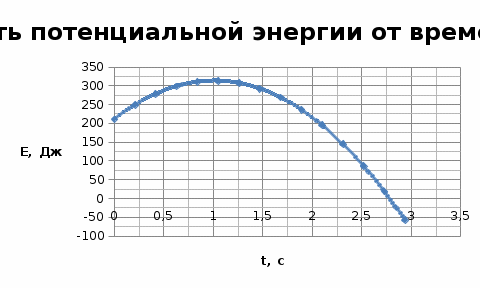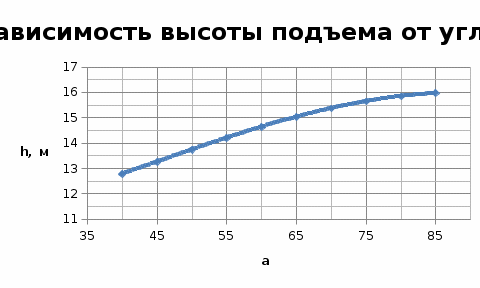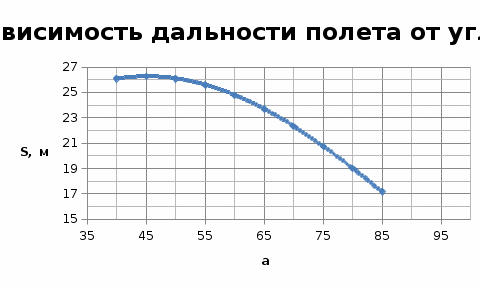   Задача №3 вариант 20 Брусок с трением скатывается по наклонной плоскости и продолжает двигаться горизонтально по гладкой поверхности до полной остановки. Определить полное расстояние, пройденное бруском, время движения, кинетическую энергию в момент скатывания с наклонной плоскости. Построить график зависимости пройденного расстояния от угланаклона плоскости в интервале от α0доαс шагом 5° при коэффициенте трения μ0 и от коэффициента трения в интервале от μ0 до μ с шагом h, приугле наклона α0. Дано: m=1,8 кг; Н=0,33 м; α0= 40º; α=65º; μ0=0,44; μ=0,49. Решение. Определить полное расстояние, пройденное бруском, время движения, кинетическую энергию в момент скатывания с наклонной плоскости. 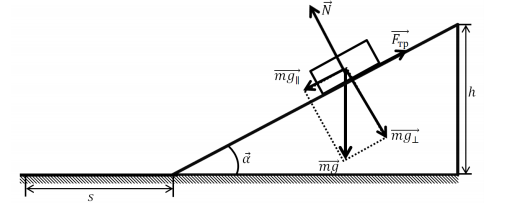 Определим полное расстояние, пройденное бруском. Для решения данной задачи необходимо использовать закон сохранения энергии и второй закон Ньютона. Потенциальная энергия бруска в начале пути будет равна:  Работа, совершаемая бруском, против сил трения, действующих на всем участке пути:  Так как потенциальная энергия при движении расходуется на совершение работы, то можно записать:  По второму закону Ньютона:  При проецировании закона Ньютона на оси ОХ и ОУ получится система:  Из которой следует, что:    Весь пройденный путь можно найти по формуле  гдеx–расстояние, пройденное телом по наклонной плоскости, которое определяется через определение синуса угла:  s–расстояние после скатывания, которое можно найти из исходного уравнения:   Подставляя полученные результаты в формулу пройденного пути, получим:  Найдем время движения бруска. По закону движения тела с наклонной плоскости:  При условии, чтовначале движения V0=0, то  Откуда  Ускорение бруска можно найти из закона Ньютона, спроецированного на оси ОХ и ОУ  Тогда, подставляя полученное уравнение в выражение для времени, получим:  Подставляя численные результаты, получим, что время движения бруска будет:  Определим кинетическую энергиюв момент скатывания с наклонной плоскости. Наклонная сила, действующая на брусок:  Нормальная сила, действующая на брусок:  Сила трения, действующая на брусок:  Результирующая сила направлена вдоль наклонной плоскости:  Результирующая сила, действующая на брусок, равна 2,25 Н и действует она на всем пути бруска–x=0,51 метров. При этом результирующая сила совершает работу:  Эта работа тратится на ускорение бруска и преобразуется в кинетическую энергию:  Построим график зависимости пройденного расстояния от угла наклона плоскости в интервале от α0доαс шагом 5° при коэффициенте трения μ0 и график зависимости пройденного расстояния от коэффициента трения в интервале от μ0 до μ с шагом h, при угле наклона α0. График зависимости пройденного расстояния от угла наклона плоскости в интервале от α0=35º до α=60º с шагом 5° при коэффициенте трения μ0=0,22: 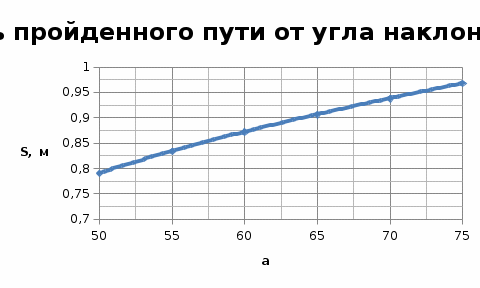 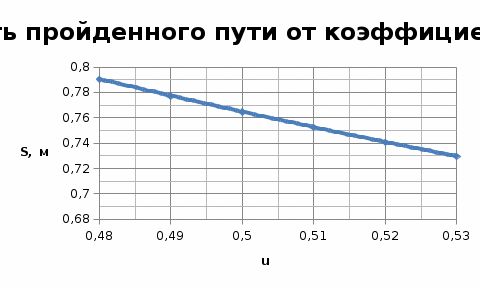 Задача №4 вариант 20 Изотермический процесс протекает при температуре T. Постройте график процесса, если известно, что давление газа изменяется от p0 до p, а начальный объем равен V0. Дано: P0 = 62 Па, P = 21 Па V= 4,8 м3 T = 302 K Изотермический процесс протекает при постоянной температуре. Уравнение процесса: PV=RT=const V= const/P Давление изменяется от P0 до P. PV=297,6 = const V=297,6/P Таблица для построения графика.
 |