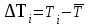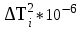Вариант № 26. Задача 1 Задание
 Скачать 121.57 Kb. Скачать 121.57 Kb.
|
Вариант № 26Задача № 1Задание: При градуировке средства измерения с линейной функциональной характеристикой получены числовые значения экспериментальных данных (таблица 1). По полученным данным найти методом наименьших квадратов аналитические выражения для градуировочной характеристики и построить ее графически. Таблица 1 – Экспериментальные данные
Решение: 1) Линейная градуировочная характеристика описывается выражением: Y = а0 + а1∙X, где коэффициенты а0 и a1 методом наименьших квадратов находятся по формулам: a0 = 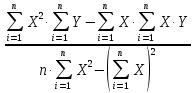 , ,a1 = 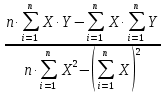 . .Находим параметры уравнения методом наименьших квадратов: Система уравнений МНК: a0n + a1∑х = ∑y a0∑х + a1∑х2 = ∑y·х
Для имеющихся данных система уравнений имеет вид: 10 a0 + 225a1 = 1941,7 225 a0 + 7125a1 = 46085,0. Из первого уравнения выражаем a0 и подставим во второе уравнение. Получаем: a0 = 168,024; a1 = 1,162. Уравнение тренда: Y= 168,024 + 1,162X. Эмпирические коэффициенты тренда a0 и a1 являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных. Коэффициент тренда a1 = 1,162 показывает среднее изменение результативного показателя (в единицах измерения у) с изменением периода времени х на единицу его измерения. В данном примере с увеличением х на 1 единицу, y изменится в среднем на 1,162. Изучена временная зависимость Y от времени Х. На этапе спецификации был выбран линейный тренд. Оценены его параметры методом наименьших квадратов. Возможна экономическая интерпретация параметров модели – с каждым периодом времени Х значение Y в среднем увеличивается на 1,162 ед. изм. Графически уравнение тренда построено на рисунке 1, где точками нанесены экспериментальные данные. 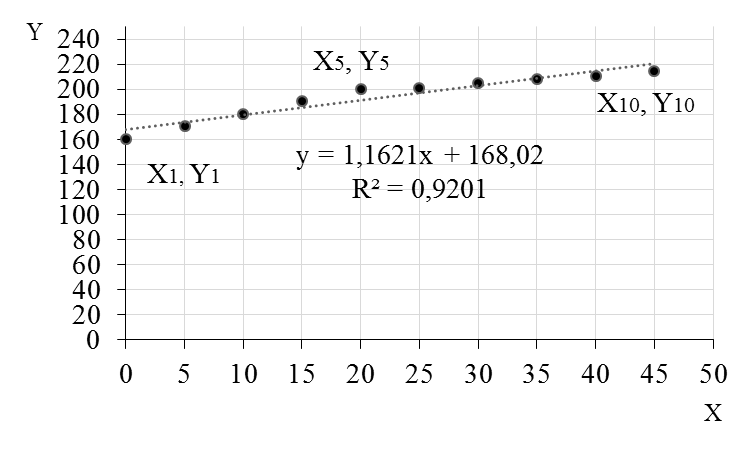 Рисунок 1 – Градуировочная характеристика Задача № 2 Задание: По экспериментальным данным (таблица 2) многократных наблюдений при прямом измерении параметра X, вычислить результат измерения – 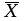 и его случайную составляющую погрешности ∆, при Pα = 0,68 (tα = 1), Pα = 0,95 (tα = 2), Pα = 0,997 (tα = 3). и его случайную составляющую погрешности ∆, при Pα = 0,68 (tα = 1), Pα = 0,95 (tα = 2), Pα = 0,997 (tα = 3).Таблица 2 – Экспериментальные данные наблюдения температуры
Решение: 1) Определим 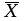 по формуле: по формуле: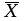 = = 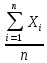 , ,где X1, Х2, ... Xi ... Хn – массив экспериментальных данных. Согласно априорной информации, систематических составляющих погрешностей нет, а разброс наблюдений подчиняется нормальному закону распределения вероятностей. Тогда параметры наблюдений температуры составят: 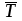 = 1,89 °С. = 1,89 °С.2) Рассчитаем среднее квадратическое отклонение (СКО) результата многократного измерения определяется зависимостью: σ = 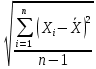 . .σ = 0,59 ºС. Для среднего арифметического результата измерения: 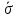 = = 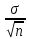 . .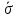 = 0,187 ºС. = 0,187 ºС.3) Рассчитаем оценку случайной составляющей погрешности по формуле: ∆ = 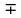 tα∙ tα∙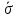 , ,а) с доверительной вероятностью Pα = 0,68 (tα = 1): ∆ = ±1 * 0,187 = ± 0,187 ºС, т.е. после округления результат измерения температуры можно представить в одном из двух вариантов: 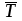 = 1,89 °С; ∆ = ±0,19 °С; Рα = 0,68 или = 1,89 °С; ∆ = ±0,19 °С; Рα = 0,68 или 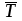 = (1,89 ± 0,19) °С; Рα = 0,68. = (1,89 ± 0,19) °С; Рα = 0,68.Относительная ошибка: δ = 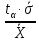 ∙100%, ∙100%, где tα – коэффициент Стьюдента, определяемый доверительной вероятностью α δ = 0,187/ 1,89 * 100% ≈ 9,9%. б) с доверительной вероятностью Pα = 0,95 (tα = 2): ∆ = ±2 * 0,187 = ± 0,374 ºС, т.е. после округления результат измерения температуры можно представить в одном из двух вариантов: 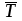 = 1,89 °С; ∆ = ±0,37 °С; Рα = 0,95 или = 1,89 °С; ∆ = ±0,37 °С; Рα = 0,95 или 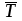 = (1,89 ± 0,37) °С; Рα = 0,95. = (1,89 ± 0,37) °С; Рα = 0,95.Относительная ошибка: δ = 0,374/ 1,89 * 100% ≈ 19,8%. в) с доверительной вероятностью Pα = 0,997 (tα = 3): ∆ = ±3 * 0,187 = ± 0,561 ºС, т.е. после округления результат измерения температуры можно представить в одном из двух вариантов: 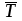 = 1,89 °С; ∆ = ±0,56 °С; Рα = 0,997 или = 1,89 °С; ∆ = ±0,56 °С; Рα = 0,997 или 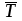 = (1,89 ± 0,56) °С; Рα = 0,997. = (1,89 ± 0,56) °С; Рα = 0,997.Относительная ошибка: δ = 0,374/ 1,89 * 100% ≈ 19,8%. Задача № 3Задание: Определить страну происхождения товара и подлинность штрих-кодов. Решение: 1) Страна происхождения Россия:  2) Применим первый метод: а) двигаясь справа налево, суммируем все цифры на четных позициях: 3 + 0 + 4 + 8 + 7 + 6 = 28; б) умножаем полученный результат на 3: 28 * 3 = 84; в) суммируем цифры на нечетных позициях. Начинаем с третьей по счету цифре: 6 + 1 + 6 + 0 + 0 + 4 = 17; г) суммируем результаты, полученные в пунктах б и в: 84 + 17 = 101; д) округлим полученный результат в большую сторону до ближайшего кратного десяти. В данном случае – это 110; е) вычтем сумму, полученную при вычислениях в пункте г: 110 - 101 = 9; 3) Полученный результат соответствует контрольной (последней) цифре штрих-кода – 9, что говорит о подлинности товара. Задача № 4Задание: По экспериментальным данным представленным в таблице 3 построить диаграмму разброса, рассчитать коэффициент корреляции и оценить его достоверность. Таблица 3 – Экспериментальные данные
Решение:
Таблица – Результаты расчетов 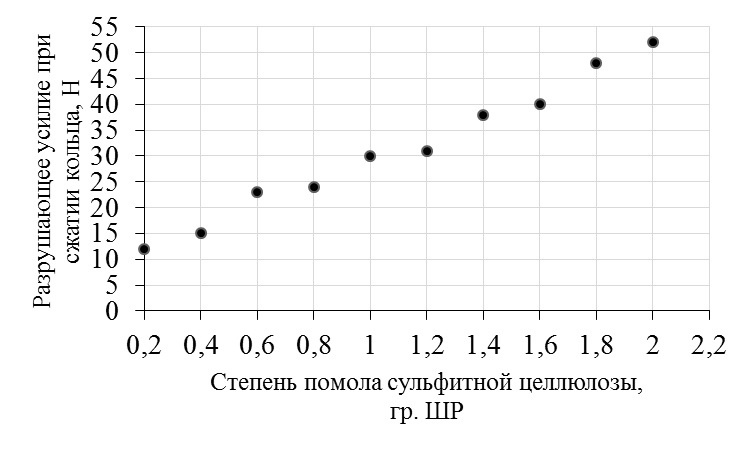 Рисунок 2 – Зависимость разрушающего усилия при сжатии кольца от степени помола сульфитной целлюлозы 1) Для установления силы связи между величинами XY используем коэффициент корреляции, определяемый по следующей формуле: r = 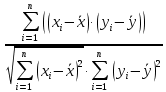 , ,где r – коэффициент корреляции; хi – текущее значение х; yi – текущее значение y; 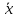 – среднее значение х; – среднее значение х;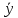 – среднее значение у; – среднее значение у;n – объем выборки. r = 0,99. Можно сделать вывод, что между величинами существует сильная положительная корреляция. 2) Оценим достоверность коэффициента корреляции. Для этого вычислим его среднюю ошибку m, по формуле: mr = 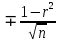 , ,при r/mr > 3 коэффициент корреляции считается достоверным, т.е. связь доказана. При r/mr < 3 связь считается недостоверной. mr = ± 0,01. r/mr = 99. Коэффициент корреляции считается достоверным, т.е. связь доказана. Список литературы Алексеева В.В. Метрология, стандартизация и сертификация: учебник / В.В. Алексеева. – М.: Изд. центр «Академия», 2007. – 384 с. Гончаров А.А. Метрология, стандартизация и сертификация / А.А. Гончаров, В.Д. Копылов – М.: Академия, 2008. – 240 с. Клевлеев В.М. Метрология, стандартизация и сертификация / В.М. Клевлеев, Ю.П. Попов, И.А. Кузнецова. – М.: Форум, Инфра-М, 2004. – 378 с. Колчков В.И. Метрология, стандартизация и сертификация / В.И. Колчков. – М.: Владос, 2010. – 298 с. Кондрашкова Г.А. Метрология. Стандартизация. Сертификация. Квалиметрия. Практикум: учебно-методическое пособие / Г.А. Кондрашкова, И.В. Бондаренкова, Е.П. Дятлова. – СПб: ВШТЭ СПбГУПТД, 2019. – 114 с. Радкевич Я.М. Метрология, стандартизация и сертификация: учебник / Я.М. Радкевич, А.Г. Схиртладзе, Б.И. Лактионов. – М.: Высшая школа, 2006. – 798 с. Сергеев А.Г. Метрология, стандартизация и сертификация: учебное пособие / А.Г. Сергеев, М.В. Латышев, В.В. Терегеря В.В. – М.: Логос, 2009. – 560 с. Хрусталева З.А. Метрология, стандартизация и сертификация. Практикум / З.А. Хрусталева. – Кнорус, 2011. – 176 с. |

 [ºС]
[ºС]