задача. Задача 10
 Скачать 108 Kb.
|
|
ТРЕХФАЗНЫЕ ЦЕПИ Задача 10. Определить токи, напряжения и мощности всех участков симметричной трехфазной цепи, приведенной на рис. 22. Чередование фаз прямое. Построить векторную диаграмму напряжений, совместив ее с векторной диаграммой токов. Исходные данные для расчета в соответствии с табл. 14: 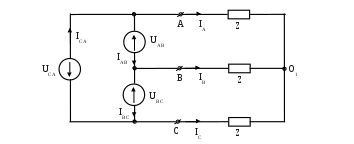  Решение: Определяем токи в фазах потребителя: 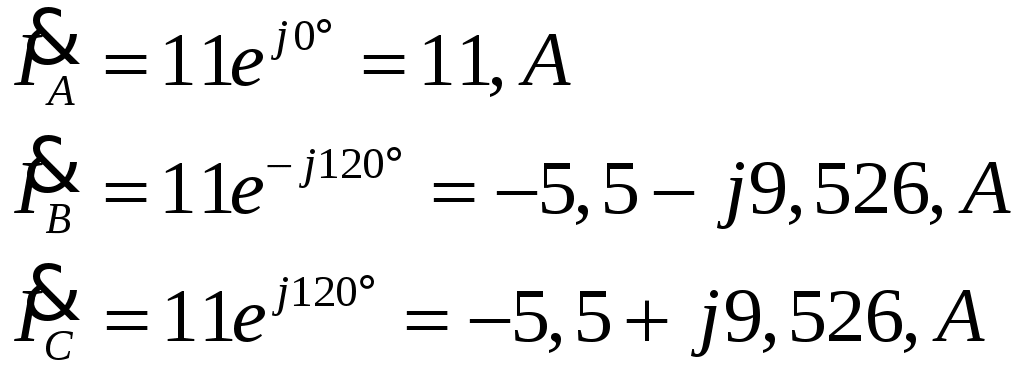 Определяем напряжения, приложенные к фазам потребителя, соединенного «звездой». При этом учитываем, что угол сдвига между ними составляет 120°: 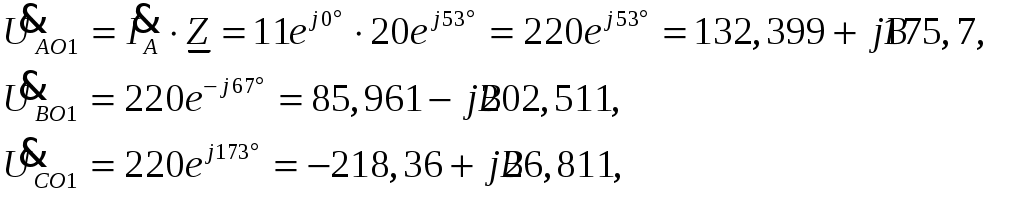 Определяем линейные напряжения источника, соединенного «треугольником». 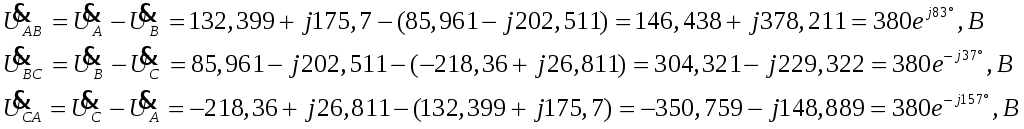 Определяем токи в источнике: 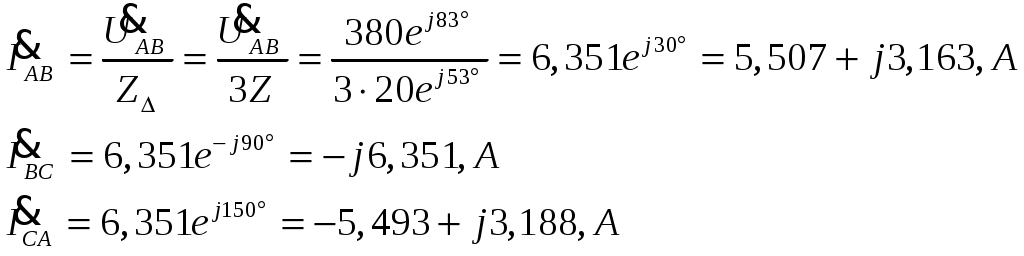 где  - сопротивление фазы потребителя, преобразованного в соединение по схеме «треугольник».Определяем активную, реактивную и полную мощности источника питания. Так как в симметричной цепи мощности всех фаз источника одинаковы, получим: 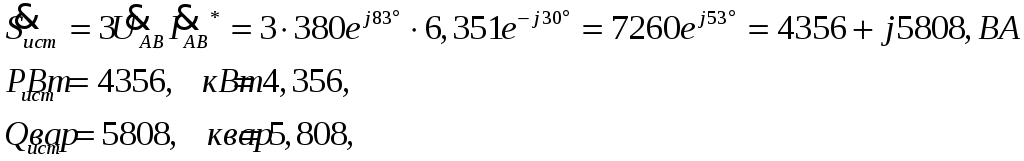 Мощность одной фазы источника, соответственно, равна: 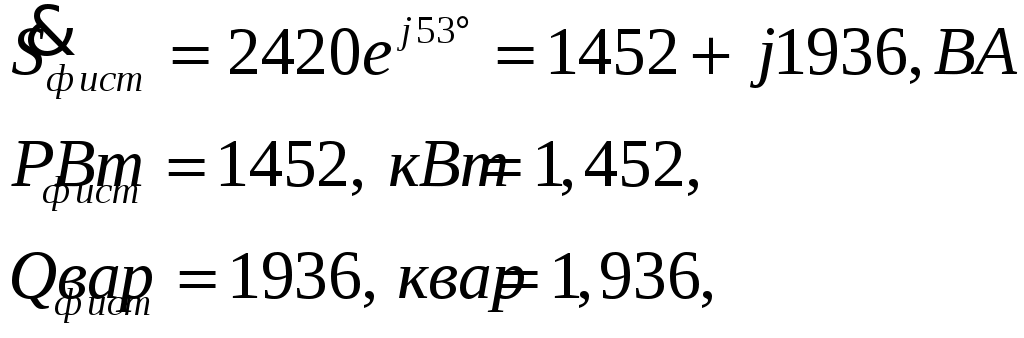 Определяем реактивную и полную мощности этого потребителя. Так как в симметричной цепи мощности всех фаз потребителей одинаковы, получим: 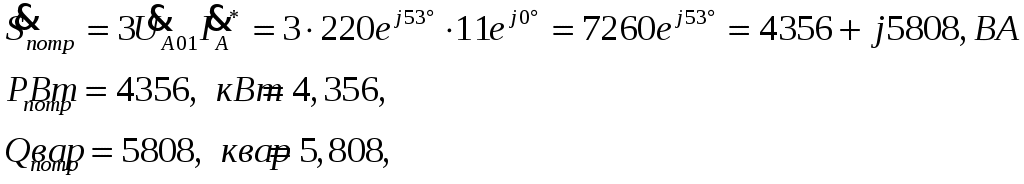 Активная, реактивная и полная мощности одной фазы потребителя, соответственно, равны: 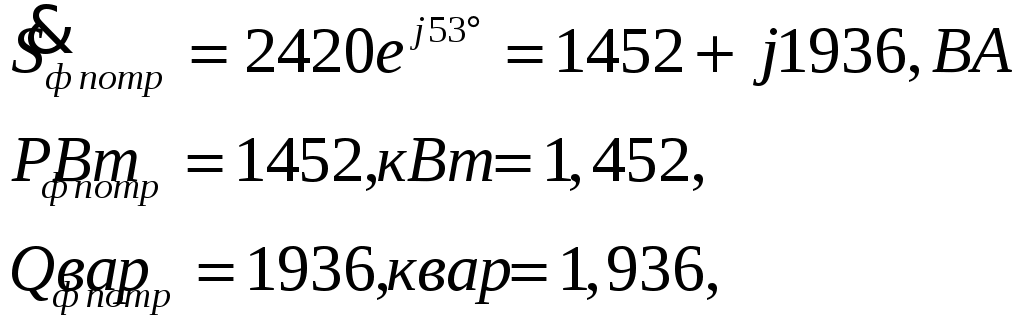 Построение векторной диаграммы напряжений, совмещенной с векторной диаграммой токов, выполним на комплексной плоскости в масштабе: по напряжению 1 см – 40 В, по току 1 см – 2,5 А. При этом учитываем, что потребитель каждой фазы носит активно-индуктивный характер, следовательно, векторы напряжений в фазах потребителей будут опережать векторы соответствующих фазных токов на угол 53°. 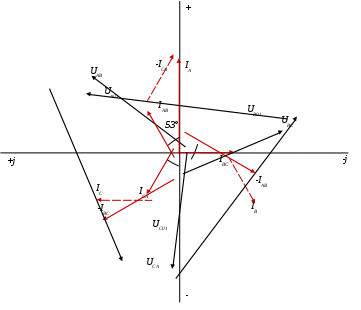 |