задача. Задача 115. Задача 115

• Название: Задача 115
• Анкор: задача
• Дата: 12.10.2022
• Размер: 37.67 Kb.
• Имя файла: Задача 115.docx
• Тип: Задача; #730202

Задача 115. Рассчитать коническую передачу с круговыми зубьями для редуктора привода ленточного транспортера (рис. 5) и проверить передачу на контактную усталость рабочих поверхностей зубьев, если мощность на ведущем валу редуктора P₁ и угловая скорость вала ω₁. Передаточное число редуктора u. Редуктор нереверсивный, предназначенный для длительной работы при постоянной нагрузке. Данные сво­его варианта принять по табл. 5. 

Рис. 5 (к задачам. 115, 129): 1 — редуктор; 2 — цепная передача; 3 — ленточный транспортер

Последовательность решения задачи:

1. Определить вращающие моменты на валу шестерни: Т₁ = 10³P₁/ω₁ и на валу колеса Т₂ = Т₁ uη, где Р₁ — в кВт; Т₁, Т₂ — в Н∙м; принять КПД конической передачи η = 0, 96.

2. Для заданной марки стали для шестерни и колеса выбрать значение твердости и предела текучести σ_т1, и σ_т2 по Приложению 1. Принять для шестерни и колеса одинаковую термообработку: улучшение поковки до твердости НВ 269... 302 и закалка ТВЧ до твердости зубьев HRC 48...53. Рекомендуется предусмотреть разность в твердости зубьев шестерни и колеса в пределах HB_1cp=HB_2ср +(20...30). Диаметр за­готовки шестерни D_пред меньше диаметра заготовки колеса.

3. Определить допускаемые контактные [σ_Н0] и изгибные [σ_F0] напряжения, соответствующие базовому числу циклов напряжений N _Н0 и N _F0 при закалке ТВЧ по контуру зубьев:

[σ_Н0] = 14HRC_cp+ 170 Н/мм²

и принять [σ_F0] = 310 Н/мм².

4. Определить допускаемые контактные и изгибные напряжения, приняв K_HL= 1 и K_FL= 1.

[σ_Н] = K_HL [σ_Н0], [σ_F]₁ = Kfl[σ_fo] ₁ и [σ_F]₂ = Kfl[σ_fo] ₂ ,

где [σ_fo] ₁ и [σ_fo] ₂ — допускаемые напряжения изгиба для шестерни и коле­са, соответствующие пределу изгибной выносливости при базовом числе циклов напряжений N_FО, которые определяются по формулам [σ_fo]₁= l,03HB_1cp и [σ_fo]₂= =l,03HB_2cp. Kfl — коэффициент долговечности при длительной работе передачи и числе циклов нагружения зубьев бо­лее базового числа циклов (N_Σ ≥N_FО= 4 • 10⁶), принять K_Fl =1.

5. Принять расчетные коэффициенты.

Коэффициенты неравномерности распределения нагрузки по длине
контакта зубьев К_Нβ и К_Fβ выбирают в зависимости от коэффициента ширины венца колёс Ψ_d=b/d₁, который определяется по формуле Ψ_d=0,166   . Принять зна­чение коэффициента неравномерности распределения нагрузки по длине
контакта зубьев К_Нβ и К_Fβ в зависимости от коэффициента ширины венца ко­леса Ψ_d при консольном расположении шестерни на роликоподшипниках по Приложениям 5 и 6.

6. Определить внешний делительный диаметр колеса из усло­вия контактной прочности зубьев по формуле d_e2= 165   ,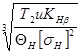

где Θ_Н = 1,3 — коэффициент вида конических колес с круговыми зубьями, Т₂—в Н∙мм, [σ_н] — в Н/мм² и d_e2— в мм.

Полученное значение d_e2округлить до ближайшего стандартного значения по ГОСТ 12289—76 из ряда нормальных линейных размеров см. Приложение 10. Принять окончательно d_e2и ширину зубчатого венца в зависимости от и или вычислить по формуле: 

7. Определить внешний окружной модуль по формуле:   ,   мм,

где Т₂— в Н∙мм, d_e2и b — в мм, Θ_F = 1 для конических колёс с круговыми зубьями, [σ_F] = [σ_F]₂ - допускаемое напряжение изгиба для материала колеса как менее прочного в Н/мм², К_Fβ – из таблиц.

Модуль зубьев передачи после его вычисления по стандарту можно
не округлять. В силовых конических передачах рекомендуется m_е ≥1,5 мм.

8. Определить число зубьев колеса и шестерни: z₂ = d_e2/m_te ; z₁ = z₂/u.

После вычисления число зубьев округлить до целого числа.

9. Уточнить передаточное число передачи u' = z₂/z₁ с точностью до сотых долей, отклонение допускается до ±3 %.

10. Определить углы делительных конусов конических колес: шестерни tgδ₁=1/u, тогда δ₁= arctg 1/u (с точностью до минуты);

колеса δ₂ = 90° — δ₁.

11. Определить коэффициенты смещения режущего инструмента, так как конические зубчатые передачи выполняют корригированными для повышения контактной прочности. По Приложению 11 определить коэффициенты смещения для шестерни х_n1 и х_е1, колеса х_n2 = - х_n1и х_е2 = - х_е1.

12. Определить геометрические размеры колес с круговыми зубьями при угле наклона зуба в середине венца β = 35°;

внешние делительные диаметры шестерни и колеса d_e1 = m_tе z₁ ;d_e2 = m_tе z₂ ;

внешние диаметры вершин зубьев колес d_ae1 = d_e1 + 1,64(1+ х_n1)m_tе cos δ₁;

d_ae2 = d_e2 + 1,64(1+ х_n2)m_tе cos δ₂;

внешнее конусное расстояние: R_e = 0,5m_te   ;

среднее конусное расстояние: R = R_e — 0,5b;

проверить условие: b/R_e < 0,285;

средний модуль: m = [m_te —(b∙sin δ₁)/z₁] cos β≈0,702m_te;

средние делительные диаметры шестерни и колеса:

d₁ = mz₁/ cos β = 0,857d_e1 и d₂ = mz₂/ cos β = 0,857d_e2.

14. Определить силы в зацеплении конических колес с круго­вым зубом:

окружная сила на шестерне и на колесе F_t = 2T₂/d₂;

радиальная сила на шестерне и осевая на колесе F_r1 = F_a2 = F_t ∙(0,44сosδ₁ - 0,7sinδ₁);

осевая сила на шестерне и радиальная на колесе F_a1 = F_r2 = F_t ∙(0,44sinδ₁ + 0,7сos δ₁).

15. Принять коэффициенты динамической нагрузки К_Нv и K_Fv по Приложению 7.

16. Проверить контактную прочность рабочих поверхностей зубьев: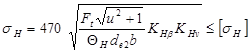

 ,где Θ_н = 1,3; F_t — в Н; d_e2, b — в мм; σ_н — Н/мм². Определить процент недогрузки или перегрузки передачи. Допускается недогрузка до 10 % или перегрузка до 5 %. В противном случае необ­ходимо изменить ширину зубчатого венца b, не выходя за пределы реко­мендуемых значений Ψ_d.

17. Определить эквивалентные числа зубьев шестерни и коле­са по формулам:

z_v1 = z₁ /(cos δ₁ cos³ β) и z_v2 = z₂ /(cos δ₂ cos³ β).

По значениям z_v1 и z_v2 выбрать коэффи­циенты формы зуба шестерни Y_Fl и колеса Y_F2 по Приложению 12 (промежуточные значения найти интерполированием).

18. Проверить прочность на изгиб зубьев шестерни и колеса

 

где принять коэффициент вида конических колес с круговыми зубьями Θ_F = 1;

F_t — в Н, b и m_е — в мм; σ_F — в Н/мм².