9 вариант. Задача 14 а) Согласно (1) дифференциальное уравнение имеет вид
 Скачать 157.5 Kb.
|
|
Вариант 9 Задача 14 а) Согласно (1) дифференциальное уравнение имеет вид  б) Это – дифференциальное уравнение 2-го порядка, так как старшая производная, входящая в уравнение, имеет порядок 2. Уравнение называется линейным, если его левая часть линейно зависит от искомой функции у, а правая часть от у не зависит. Левая часть данного уравнения линейно зависит от у, так как состоит из суммы членов вида  , где аi – константы. Правая часть данного уравнения – тождественный нуль, то есть не зависит от н. Следовательно, данное уравнение – линейное.Так как правая часть данного линейного уравнения – ноль, то оно – однородное. Наконец, это – дифференциальное уравнение с постоянными действительными коэффициентами. в) Напишем характеристическое уравнение и решим его:  Следовательно, базис линейного пространства решений состоит из двух решений:  Значит, решение уравнения будет иметь вид  Согласно начальному условию  получаем . Следовательно, решение уравнения при условии будет иметь вид  г) Анализ решения дифференциального уравнения показывает следующее. 1) Так как  , то при t решение стремится к нулю  2) Динамическая система (гармонический осциллятор) никогда при  не придет в состояние покоя, но лишь стремится к нему.3) Так как дифференциальное уравнение 2-го порядка, а дано лишь одно начальное условие, то решение описывает не единственный процесс. Задача 15 Передаточная функция есть отношение характеристических многочленов:  . Поэтому сразу пишем  . Задача 16 Уравнение можно записать в виде:  . Тогда частная реакция на воздействие  имеет вид:  , где  . Следовательно,  .Задача 17 Найдем частную реакцию методом передаточной функции, т.е. по теореме 1. Поскольку частота воздействия = 0,6, то  . Отсюда  . Тогда искомая частная реакция имеет вид  .Задача 18 б) Мы имеем линейное дифференциальное уравнение с постоянными коэффициентами. Поскольку коэффициенты уравнения знакопеременны, то отсутствует необходимый признак устойчивости. Соответственно, получаем: дифференциальное уравнение не устойчиво. а) В отличие от предыдущего случая, все коэффициенты слева положительны. Порядок уравнения больше двух. Поэтому в данном случае нужно воспользоваться тем или иным критерием устойчивости. Найдем корни характеристического уравнения  . Для этого решим характеристическое уравнение  с помощью функции polyroots в MathCAD:  . Так как действительные части всех корней отрицательны, то получаем: дифференциальное уравнение устойчиво.в) Порядок уравнения больше двух. Поэтому в данном случае нужно воспользоваться тем или иным критерием устойчивости. Найдем корни характеристического уравнения . Для этого решим характеристическое уравнение  с помощью функции polyroots в MathCAD:  . Так как  , то условие устойчивости нарушено. Соответственно, получаем: дифференциальное уравнение не устойчиво.Задача 19 Сначала убедимся в том, что дифференциальное уравнение устойчивое. Это действительно так, ибо порядок уравнения – два, и все его коэффициенты положительны. Для определения АЧХ и ФЧХ найдем передаточную функцию  .Отсюда, амплитудно-частотная характеристика (АЧХ) есть  ,фазо-частотная характеристика (ФЧХ) есть 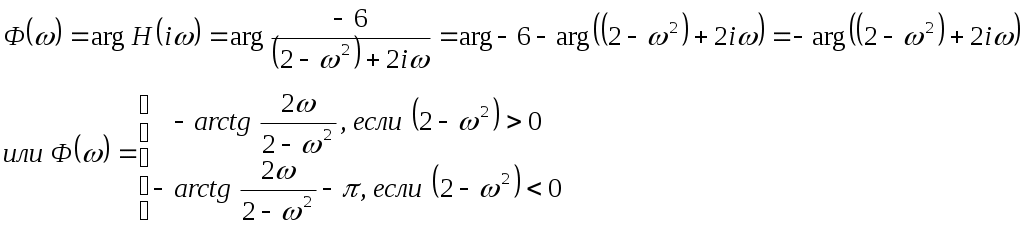 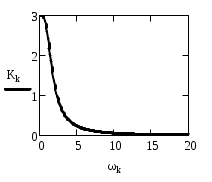 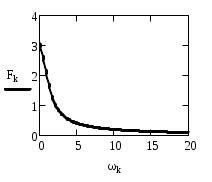 Задача 25 ЭТАП 1. Перейдем к канонической задаче Коши 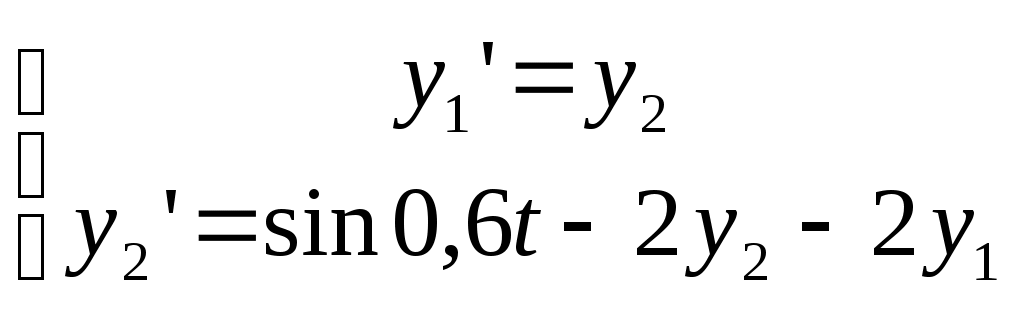 с начальными условиями  ЭТАП 2. Найдем приближенные значения решения при t0 = 0, t1 = 0,1, …, t20 = 2,0 (так как шаг h = 0,1). Для этого воспользуемся средствами MathCAD. На выходе получим таблицу значений. ЭТАП 3. По последней таблице строим ломаную Эйлера средствами MathCAD. 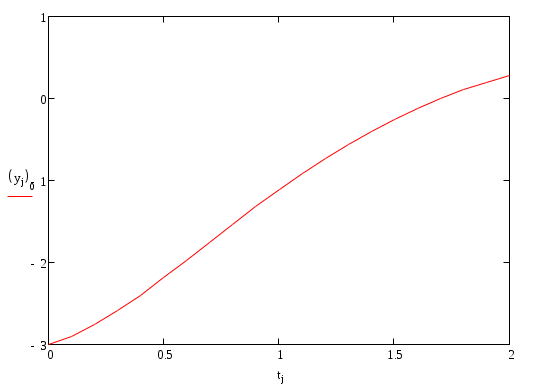    |