контрольная. 33 задачи. Задача 19. Определить относительную плотность нефтепродукта по его относительной плотности. Решение
 Скачать 101.03 Kb. Скачать 101.03 Kb.
|
|
Контрольная работа Задача 19. Определить относительную плотность нефтепродукта 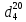 по его относительной плотности по его относительной плотности  . .Решение: Для решения задачи воспользуемся уравнением:  вычислим 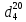 : : Задача 49. Относительная плотность нефтепродукта 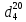 = 0,725. Найти его относительную плотность при 75 0С двумя способами. = 0,725. Найти его относительную плотность при 75 0С двумя способами.Решение: Температурная зависимость плотности нефтей и нефтепродуктов описывается уравнениями - Д. И. Менделеева (в интервале температур от 0 до 150 0С) 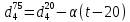 где α - средняя температурная поправка на 1 0С, которая вычисляется по формуле: 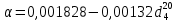 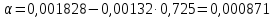 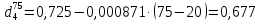 или по уравнению Мановяна: 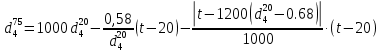 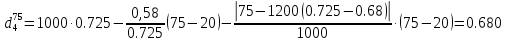 Задача 79. Определить абсолютную плотность газа гидрокрекинга при 350 0С и 900 мм рт. ст., если его молекулярная масса равна 35. Решение: По уравнению:  Задача 109. Смесь узких нефтяных фракций содержит 3 компонента, содержания которых равны соответственно (% об.) 30, 30 и 40. Плотности их 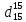 равны соответственно 0,8117; 0,8202 и 0,8301. Найти относительную плотность смеси равны соответственно 0,8117; 0,8202 и 0,8301. Найти относительную плотность смеси 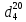 . .Решение: Средняя относительная плотность смеси жидких компонентов определяется по правилу аддитивности: 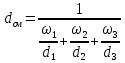 где d1, d2, d3 - относительные плотности компонентов смеси; ω1, ω2, ω3 - объёмные доли компонентов. Для решения задачи воспользуемся уравнением:  вычислим 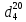 для трех плотностей: для трех плотностей: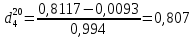  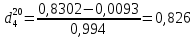 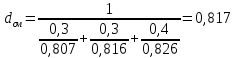 Задача 139. Вычислить среднюю молекулярную массу нефтяных фракций, имеющих средние температуры кипения 60, 138 и 165. Вычислить среднюю молекулярную массу нефтяной фракции, имеющей плотность 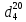 = 0,712. = 0,712.Решение: Воспользуемся уравнением Войнова: 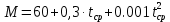 Вычислим среднюю температуру:  Тогда молекулярная масса 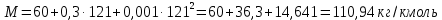 По уравнению Бриджимана: 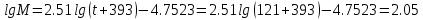  Задача 169. Определить среднюю молекулярную массу нефтепродукта, имеющего среднюю температуру кипения 250 0С и характеризующий фактор 10,8. Задачу решить двумя способами. Решение: Для нефтяных фракций с введением характеризующего фактора применима формула Войнова-Эйгенсона: 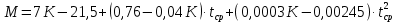 Подставляем в формулу известные величины и вычисляем молекулярную массу: 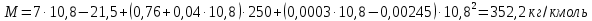 Задача 199. Смесь состоит из 21 кг н-гексана, 19 кг н-гептана и 25 кг н-октана. Определить среднюю молекулярную массу смеси. Решение: Вычислить количество молей веществ для н-гексана: 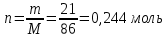 Количество молей веществ для н-гептана: 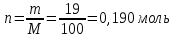 Количество молей веществ для н-октана: 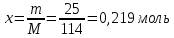 Молекулярная масса смеси по формуле равна: 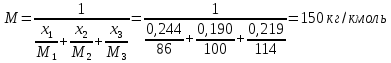 Задача 229. Определить поверхностное натяжение при 20 0С нефтяной фракции 194 – 208 0С, имеющей плотность 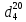 = 0,8031. Задачу решить двумя = 0,8031. Задачу решить двумяспособами. Решение: 1 способ: Поверхностное натяжение нефтепродуктов (Н/м) с относительной плотностью 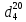 = 0,60 - 0,92 = 0,60 - 0,92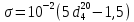  2 способ. Определим молекулярную массу по уравнению Бриджимана: 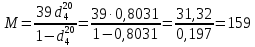 По уравнению: 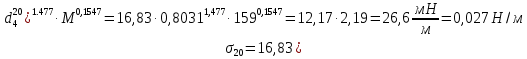 Задача 259. Кинематическая вязкость узкой нефтяной фракции при 20 0С равна 32,6 сСт, относительная плотность 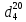 = 0,8706. Определить динамическую и условную вязкость при той же температуре. = 0,8706. Определить динамическую и условную вязкость при той же температуре.Решение: Переход между кинематической и динамической вязкостью производится по преобразованному уравнению:  в котором все параметры должны быть определены при одной температуре. Подставляем значения в формулу и вычисляем: 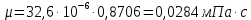 Т.к. 𝛎 <120 мм2/с (сСт), то для перехода к условной вязкости воспользуемся преобразованным уравнением:  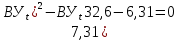 решая которое как квадратное, найдем значение условной вязкости при 20 0С. В результате решения имеем 2 корня: (0; 5,323). Корень 0 не удовлетворяет физическому смыслу задачи, поэтому условная вязкость при 20 С равна ВУ 5,323. Задача 289. Кинематическая вязкость узкой нефтяной фракции при 50 0С равна 14,00 сСт, а при 100 0С – 3,78 сСт. Определить кинематическую вязкость этой фракции при 87 0С. Задачу решить двумя способами. Решение: Воспользуемся формулой Гросса:  Для расчетов с её использованием сначала по двум имеющимся парам значений температура-вязкость вычислим значение коэффициента n: 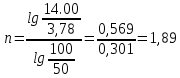 Далее, используя одну из имеющихся пар значений температура-вязкость и заданную температуру, определим вязкость при заданной температуре: 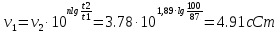 Решим эту же задачу с помощью уравнения Вальтера:  Расчет коэффициентов a и b производится по уравнениям: 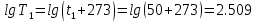   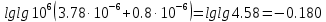 Коэффициент b: 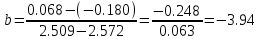 Коэффициент a:  Таким образом, температурная зависимость вязкости нефтяной фракции имеет вид:  При 87 0С правая часть уравнения равна: 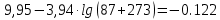 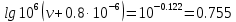 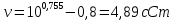 Задача 319. Кинематическая вязкость узкой нефтяной фракции при атмосферном давлении v20 = 96,29 сСт. Определить вязкость фракции при той же температуре и 1,72 кгс/см2. Решение: Зависимость вязкости от давления описывается уравнением Манстона. Вязкость (сСт) при повышенном давлении вычислим по преобразованному уравнению Манстона:  Задача 349. Определить вязкость смеси, состоящей из 47 % (масс.) фракции с вязкостью 90 сСт и 53 % (масс.) фракции с вязкостью 180 сСт. Решение: Для расчета вязкости смеси воспользуемся уравнением:   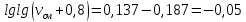 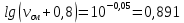  Задача 379. Определить кинематическую и динамическую вязкость неопентана при 245 0С и атмосферном давлении; при 245 0С и 5,2 атм. Решение: Вязкость паров неопентана при нормальных условиях определим по уравнению: 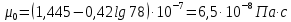 Критические параметры для бензола найдем в таблице 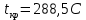 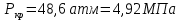 Вычислим приведенные параметры:  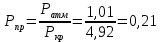 Воспользуемся номограммой, представленной на рисунке 5.3. На шкале 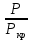 отмечаем точку 0,021; на шкале отмечаем точку 0,021; на шкале 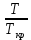 - точку 0,923. Через две точки проводим прямую до пересечения со шкалой - точку 0,923. Через две точки проводим прямую до пересечения со шкалой  - она соответствует значению1,2. - она соответствует значению1,2.То есть  тогда  При давлении Р=5,2 атм = 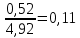 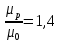  Задача 409. Разгонка по Энглеру фракции 70 – 200 0С минчимкинской нефти дает следующие результаты:
Определить СМТК, СВТК, СКТК и СУТК. Решение: Построим график разгонки по Энглеру. t=f(V)  По исходным данным определяем температуру 50 % выкипания по Энглеру  Температурную разность вычисляем по формуле: 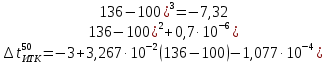 Температура 50 % выкипания по ИТК определяется по формуле: 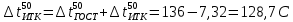 Задача 439. Определить координаты кривой ИТК по известной кривой разгонки на аппарате Энглера фракции 28 – 170 0C орловской нефти ( 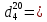 0,7709) 0,7709)
Решение: Построим график разгонки по Энглеру. t=f(V)  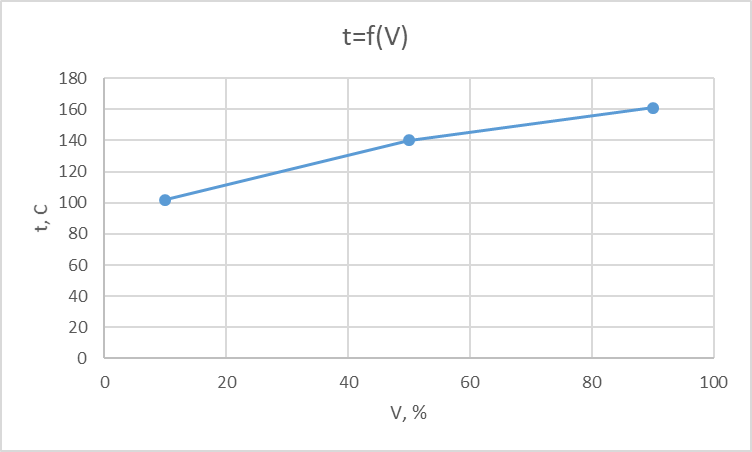 Составим новую таблицу, в которую внесем точки 0, 10, 30, 50, 70, 90 % (интерполяция недостающих значений 30 и 70 % по графику) выкипания и температуры им соответствующие.
По исходным данным определяем температуру 50 % выкипания по Энглеру 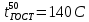 Температурную разность вычисляем по формуле:  Температура 50 % выкипания по ИТК определяется по формуле:  Вычисление величин 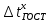 производится следующим образом. От каждой последующей температуры отнимается предыдущая. Вычисления заносятся в таблицу, напротив производится следующим образом. От каждой последующей температуры отнимается предыдущая. Вычисления заносятся в таблицу, напротив  ставится прочерк. ставится прочерк.Далее для каждого значения 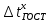 путем решения уравнения отыскивается значение путем решения уравнения отыскивается значение  (коэффициенты уравнения берутся из таблицы для каждого интервала отгона). Значения (коэффициенты уравнения берутся из таблицы для каждого интервала отгона). Значения заносятся в таблицу причем, соответствующие отгону до 50 % со знаком «минус», а соответствующие отгону свыше 50 % с сохранением положительного значения. Для отгона 50 % заносятся в таблицу причем, соответствующие отгону до 50 % со знаком «минус», а соответствующие отгону свыше 50 % с сохранением положительного значения. Для отгона 50 %заносится ранее определенное  . .Рассмотрим подробно решение уравнения для интервала 0 – 10 %. Используя коээфициенты из таблицы, получим общий вид уравнения:  Для упрощения вида уравнения обозначим  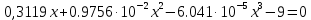 Для решения полученного уравнения применим графический метод. Составим таблицу значений функции  задаваясь значениями x в интервале  целых чисел. целых чисел.
По данным полученной таблицы строим график 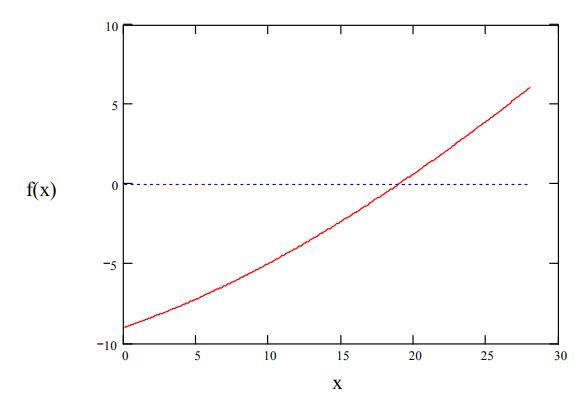 и находим абсциссу точки пересечения кривой с осью абсцисс. Эта точка и есть искомый корень уравнения. В данном случае 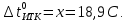 Задача 469. Определить теплоемкость жидкого нефтепродукта плотностью 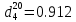 при температуре 105 0С. Задачу решить двумя способами. при температуре 105 0С. Задачу решить двумя способами.Решение: Перейдем к 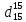 по уравнению: по уравнению: По уравнению Крэга:  По уравнению: 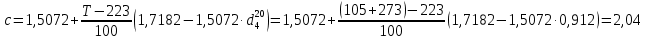 По номограмме, изображенной на рисунке при 105 0С и 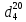 = 0,912 по шкале для жидкости с=2,1 кДж/кгК. = 0,912 по шкале для жидкости с=2,1 кДж/кгК.Задача 499. Определить теплоемкость нефтяной фракции, имеющей tср = 240 0С и 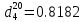 , при 125 0С. , при 125 0С.Решение: Перейдем к плотности 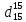 по уравнению: по уравнению: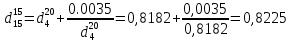 Допустим, что tср куб = tср, тогда характеризующий фактор Ватсона по уравнению: 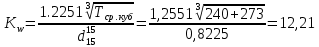 По уравнению Фаллона-Ватсона: 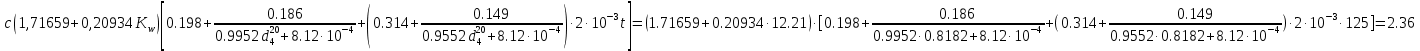 Задача 529. Определить теплоемкость паров нефтепродукта плотностью  при 265 0С и атмосферном давлении. Задачу решить двумяспособами. при 265 0С и атмосферном давлении. Задачу решить двумяспособами.Решение: Перейдем к плотности 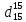 по уравнению: по уравнению: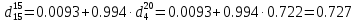 Воспользуемся формулой Бальке и Кей:  По номограмме, изображенной на рисунке при  по шкале паров и 265 0С. по шкале паров и 265 0С.с=2,0 кДж/(кг·К). Задача 559. Определить при 270 0С и 5,5 атм теплоемкость паров нефтепродукта, имеющего 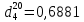 , tкр = 215 0С, Pкр = 32 атм и K =12,0. , tкр = 215 0С, Pкр = 32 атм и K =12,0.Решение: Перейдем к плотности 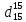 по уравнению: по уравнению: Воспользуемся формулой Бальке и Кей: 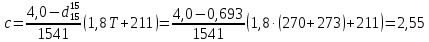 Вычислим приведенные температуру и давление: 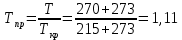 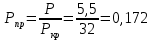 По графику, изображенному на рисунке определим поправку к теплоемкости на давление: ∆с=4,0 кДж/кмольК Молярную массу фракции найдем по формуле Крэга: 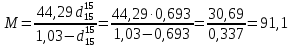 Пересчитаем поправку с мольной размерности на массовую:  Таким образом, теплоемкость паров под давлением равна: 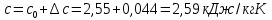 Задача 589. Определить теплоемкость смеси, состоящей из 25 кг нефтепродукта теплоемкостью 2,41 кДж/(кг·К) и 27 кг нефтепродукта теплоемкостью 0,537 ккал/(кг·К). Решение: Вычислим массу смеси mсм=25+27=52 кг Следовательно, массовые доли равны: 0,537 ккал/(кг·К) ·4,184 = 2,25 кДж/(кг·К) 1 ккал - 4,184 кДж Найдем теплоёмкость смеси по формуле: 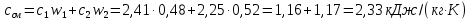 Задача 619. Определить теплоту испарения нефтяной фракции, имеющей tср.мол=123 0С и 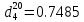 при атмосферном давлении. Задачу решить двумя способами. при атмосферном давлении. Задачу решить двумя способами.Решение: По уравнению Кистяковского теплота испарения (кДж/кмоль) равна:  Мольную массу фракции определим по формуле Войнова: 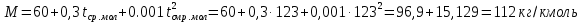 Тогда, вычисленная по уравнению Кистяковского теплота испарения (кДж/кг) равна: 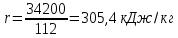 Перейдем к относительной плотности 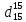 по уравнению: по уравнению: Тогда по уравнению Уэйра и Итона теплота испарения (кДж/кг) равна:  Характеризующий фактор вычислим по уравнению: 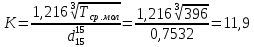 По графику, представленному на рисунке 10.2, теплота испарения равна: r = 3,08 кДж/кг. Задача 649. Определить теплоту испарения циклопентана при 2,4 атм. Решение: 1 атм=0,1 МПа 2,4 атм = 0,24 МПа По справочным данным определим, что нормальная температура кипения циклопентана равна 49 0С. Вычислим значение комплекса  Используя график, изображены на рисунке 10.1, по кривой для углеводородов определим:  откуда 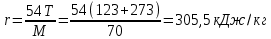 Задача 679. Определить энтальпию жидкой нефтяной фракции, имеющей 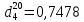 , при 65 0С. , при 65 0С.Решение: Перейдем к относительной плотности 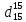 по уравнению: по уравнению: По уравнению Фортча и Уитмена: 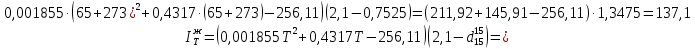 По уравнению Крэга:  Задача 709. Определить энтальпию паров нефтепродукта плотностью 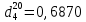 при 140 0С и атмосферном давлении. при 140 0С и атмосферном давлении.Решение: Перейдем к относительной плотности 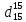 по уравнению: по уравнению: По уравнению: 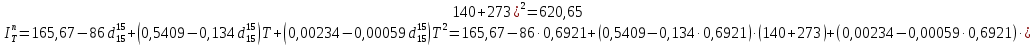 По уравнению: 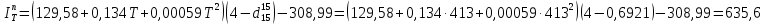 Задача 739. Определить энтальпию паров нефтяной фракции, имеющей  , tср =109 0С, tкр = 295 0С, Pкр = 25,5 атм, при 190 0С и 4,1 кгс/см2. , tср =109 0С, tкр = 295 0С, Pкр = 25,5 атм, при 190 0С и 4,1 кгс/см2.Решение: 4,1 кгс/см2=0,402 МПа Перейдем к относительной плотности 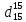 по уравнению: по уравнению: Энтальпию паров при атмосферном давлении найдем по уравнению:   Вычислим приведенные параметры: 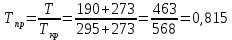 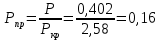 Поправку к энтальпии на давление вычислим по уравнению: 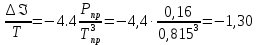 Молекулярную массу фракции вычислим по формуле Бриджимана: 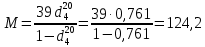 Таким образом, из уравнения 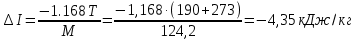 Тогда энтальпия паров при повышенном давлении равна: 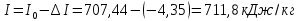 Задача 769. Определить теплопроводность фракции 165 – 200 0С, имеющей  при температуре 150 0С. при температуре 150 0С.Решение:  Перейдем к относительной плотности 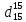 по уравнению: по уравнению: По формуле Абросимова: 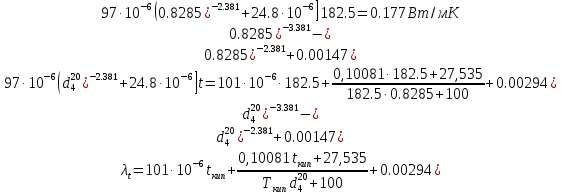 Задача 799. Определить теплопроводность пропана при 100 0С и 1,4 МПа. Решение: Критические параметры амилена найдем в таблице: tкр=96,8 0С Ркр=42 атм=4,26 МПа Теплопроводность при атмосферном давлении найдем по формуле Мизика и Тодоса: 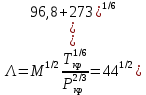 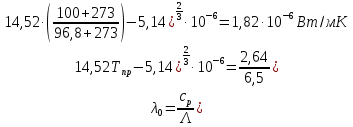 Задача 829. Определить давление насыщенных паров фракции 160 – 172 0С, имеющей относительную плотность  при 170 0С. Задачу решить всеми возможными способами и сравнить результаты. при 170 0С. Задачу решить всеми возможными способами и сравнить результаты.Решение: 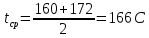 Вычислим ДНП по формуле Вильсона, рассчитав предварительно коэффициенты А и В по уравнениям  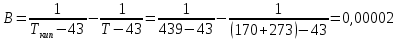  Вычислим ДНП фракции по уравнению Ашворта, предварительно определив значения вспомогательных величин по уравнениям 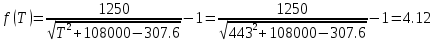   Для определения ДНП по уравнению вычислим вспомогательные величины:   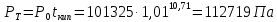 Рассчитанные значения давления близки. Задача 859. Узкая нефтяная фракция при атмосферном давлении имеет температуру кипения 130 0С. Какова температура кипения этой фракции при давлении 1150 мм рт. ст. При каком давлении температура кипения фракции будет равна 115 0С? Решить задачу графическим и аналитическим способами. Решение: Кипение жидкости наступает тогда, когда давление её насыщенных паров сравнивается с внешним давлением. По уравнению вычислим вспомогательную величину:  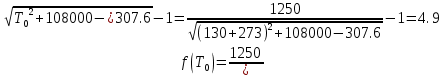 Воспользуемся преобразованным уравнением Ашворта 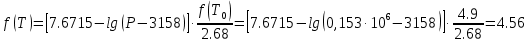 Температуру кипения (С) при повышенном давлении найдем из преобразованного уравнения: 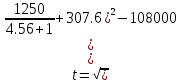 Пользуясь номограммой, представленной на рисунке, получим, что t=152 0С. Задача 889. Определить фугитивности жидкой нефтяной фракции 88 – 106 0С и её паров при 100 0С и 1000 мм рт. ст., если tкр = 275 0С, Pкр = 26,5 атм. Решение: Вычислим приведенные параметры для пара:  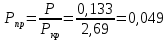 По графику, изображенному на рисунке 14.1 находим, что при Tпр = 0,68 и Pпр = 0,049: γ=0,92 Тогда фугитивность пара по уравнению: f = γP = 0,92 · 0,133 = 0,12 МПа. Приведенное давление для жидкости: 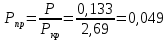 Фугитивность жидкости по уравнению: fж = 0,92 · 0,133 = 0,12 МПа Задача 919. Определить критические температуру и давление для фракции 28 –200 0С колендинской нефти, имеющей плотность 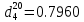 . Задачу решить всеми возможными способами. . Задачу решить всеми возможными способами.Решение: 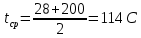 Перейдем к относительной плотности 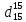 по уравнению: по уравнению: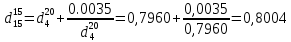 Для расчета критической температуры по уравнению Итона и Портера вычислим вспомогательную величину по уравнению: 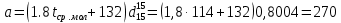 Тогда критическая температура (К): 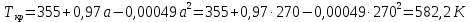 По уравнению Максвелла:  По графику, представленному на рисунке 15.2: tкр = 471 С. Задача 949. Определить константу фазового равновесия изобутана при 65 0С и 1050 мм рт. ст. Решение: Константа фазового равновесия для идеальной системы вычисляется по уравнению, используя давление насыщенных паров и общее давление в системе: 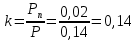 Номограмма для определения констант фазового равновесия углеводородов при низких температурах при 140 кПа и t=65 С k=0,15 Задача 979. Рассчитать константу фазового равновесия узкой нефтяной фракции 95 – 122 0С плотностью  при 145 0С и 2,6 кгс/см2 и определить её значение по номограмме. при 145 0С и 2,6 кгс/см2 и определить её значение по номограмме.Решение: 2,6 кгс/см2=255 кПа Критические параметры tкр = 234,7 ˚С, Ркр=2,94 МПа. Определяем фугитивность паров при 145 ˚С и 255 кПа. Приведенные температура и давление равны: 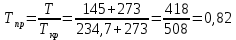 На рис. по найденным Тпр и Рпр находим, что коэффициент активности γ=0,92, отсюда: Фугитивность жидкости по уравнению: fж = 0,92 · 0,133 = 0,12 МПа Определяем фугитивность жидкого при 145 ˚С и давлении собственных паров Р=0,255 МПа. Приведенное давление равно: Приведенное давление для жидкости:  fж = 0,92 · 0,087 = 0,40 МПа Величина константы фазового равновесия равна: 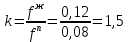 Номограмма для определения констант фазового равновесия углеводородов при низких температурах при 255 кПа и t=145 С Номограмма для определения констант фазового равновесия углеводородов при низких температурах при 255 кПа и t=145 Сk=1,8 |
