Задача 19 расчеты на удар схема 20 (Строка 17)
 Скачать 230.57 Kb. Скачать 230.57 Kb.
|
|
ЗАДАЧА № 19 РАСЧЕТЫ НА УДАР Схема 20 (Строка 17) Для системы, на которую падает груз Q с высоты h, пренебрегая массой стержней, найти динамический коэффициент и максимальное нормальное напряжение в опасном сечении. Примечание. 1. Величина статистического перемещения в месте удара находится с помощью способа Верещагина. 2. Для схем № 1−5 и № 11−20 следует начертить схему системы в деформированном состоянии. При решении задачи использовать таблицу исходных данных (с. 61) и расчетные схемы на с. 62–64. Дано ∶ 𝑄 = 11кН; 𝑎 = 2.4 м; 𝑏 = 3.6 м; 𝑙 = 5.4 м; 𝑙1 = 6.0 м; 𝑙2 = 7.0 м; 𝐴1 = 8.0 см2; 𝐴2 = 6.0 см2 ; ℎ = 11 см; Сечение балка − Двутавр №55; 𝐼𝑧 = 55962 см4; 𝑊𝑧 = 2035 см3; 𝐴 = 118 см2 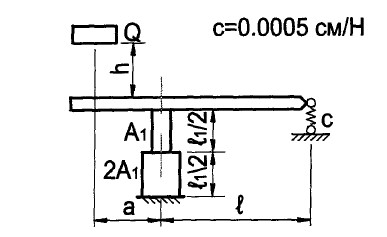  Решение: 1) Приклаываем вертикальную силу равную единицу в балке месте удара и строим эпюру единичных изгибающих моментов и единичных нормальных сил.  а) Определим реакции опоры:  Проверка: ∑ 𝐹𝑦 = −𝑃̅ + 𝑁𝐵𝐸 − 𝑌𝐶 = 0 → −1.0 + 1.4(4) + 0.4(4) = 0 → 0 = 0 Условия проверка выполняется!!! б) Строим эпюру единичных изгибающих моментов «𝑀1» 𝑀̅𝐴 = 0 𝑀̅𝐵 = −𝑃̅ ∙ 𝑎 = −1.0 ∙ 2.4 = −2.4 𝑀̅𝐶 = −𝑃̅ ∙ (𝑎 + 𝑙) + 𝑁𝐵𝐸 ∙ 𝑙 = −1.0 ∙ 7.8 + 1.4(4) ∙ 5.4 = 0 б) Строим эпюру единичных нормальных сил «𝑁1» 𝑁𝐵𝐷 = −𝑁𝐵𝐸 = −1.4(4) (Сжатие)𝑁𝐷𝐸 = −𝑁𝐵𝐸 = −1.4(4) (Сжатие) 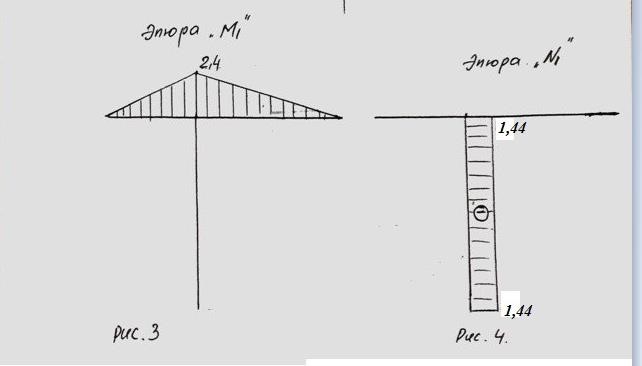 Находим единичное перемещение 𝛿11 по формулам Мора с использованием правила Верещагина путем перемножение эпюра «𝑀1» самой по себе. 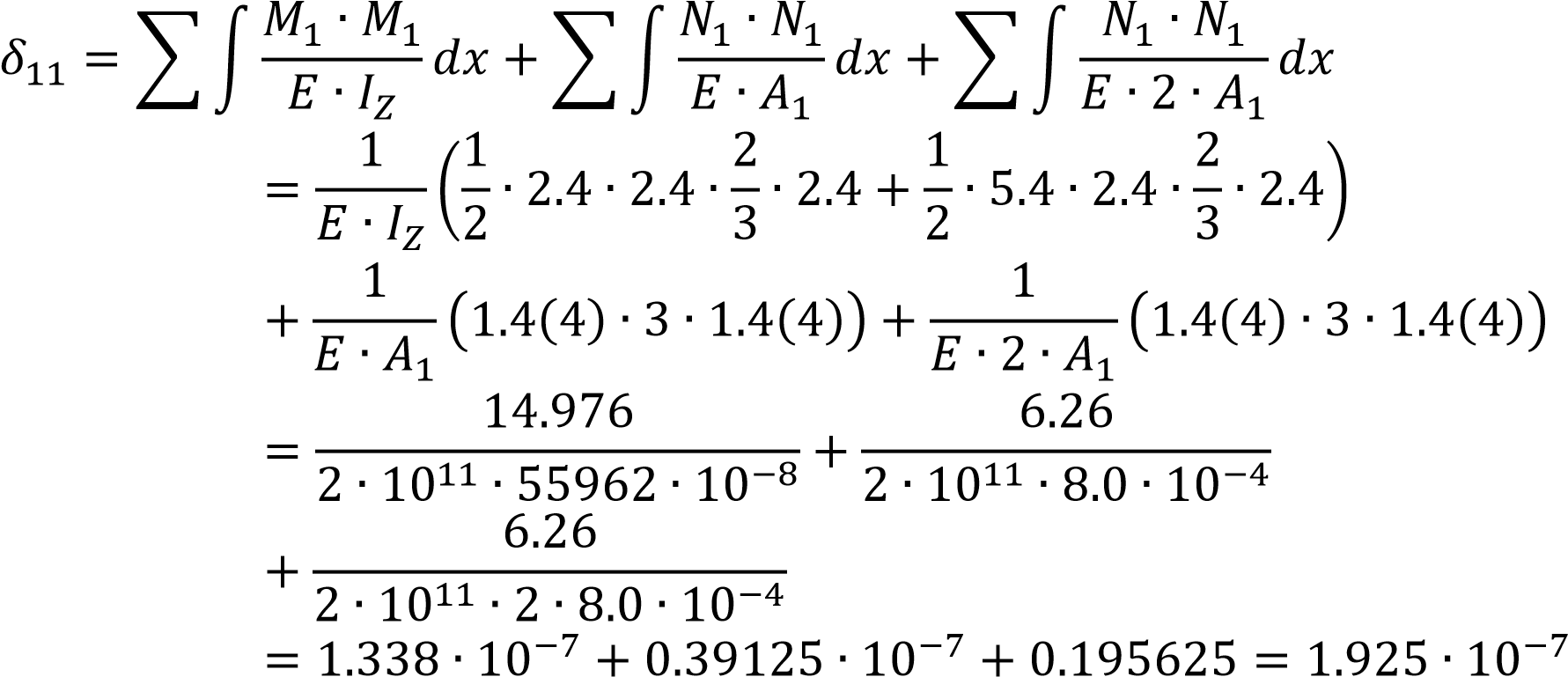 Полное перемещение от статического действия сил «Q» равен: ∆ст= ∆𝑀 + ∆пруж= 𝛿11 ∙ 𝑄 + 𝑌𝐶 ∙ 𝑄 ∙ 𝑐 = 1.925 ∙ 10−7 ∙ 11 ∙ 103 + 0.4(4) ∙ 11 ∙ 103 ∙ 0.0005 ∙ 10−2 = 21,175 ∙ 10−4 + 0,0244 = 0,0265 м = 2,65 см Определим величину динамического коэффициента  Максимальное динамические напряжение в системе Балке АС Стержень BE Прогиб балка в точке удара ∆дин= ∆ст ∙ 𝑘𝐷 = 2,65 ∙ 4,05 = 10,7325 см |
