Задача 1.2. Задача 2 Определить реакции опор составной конструкции и давление в промежуточном шарнире С
 Скачать 228.74 Kb. Скачать 228.74 Kb.
|
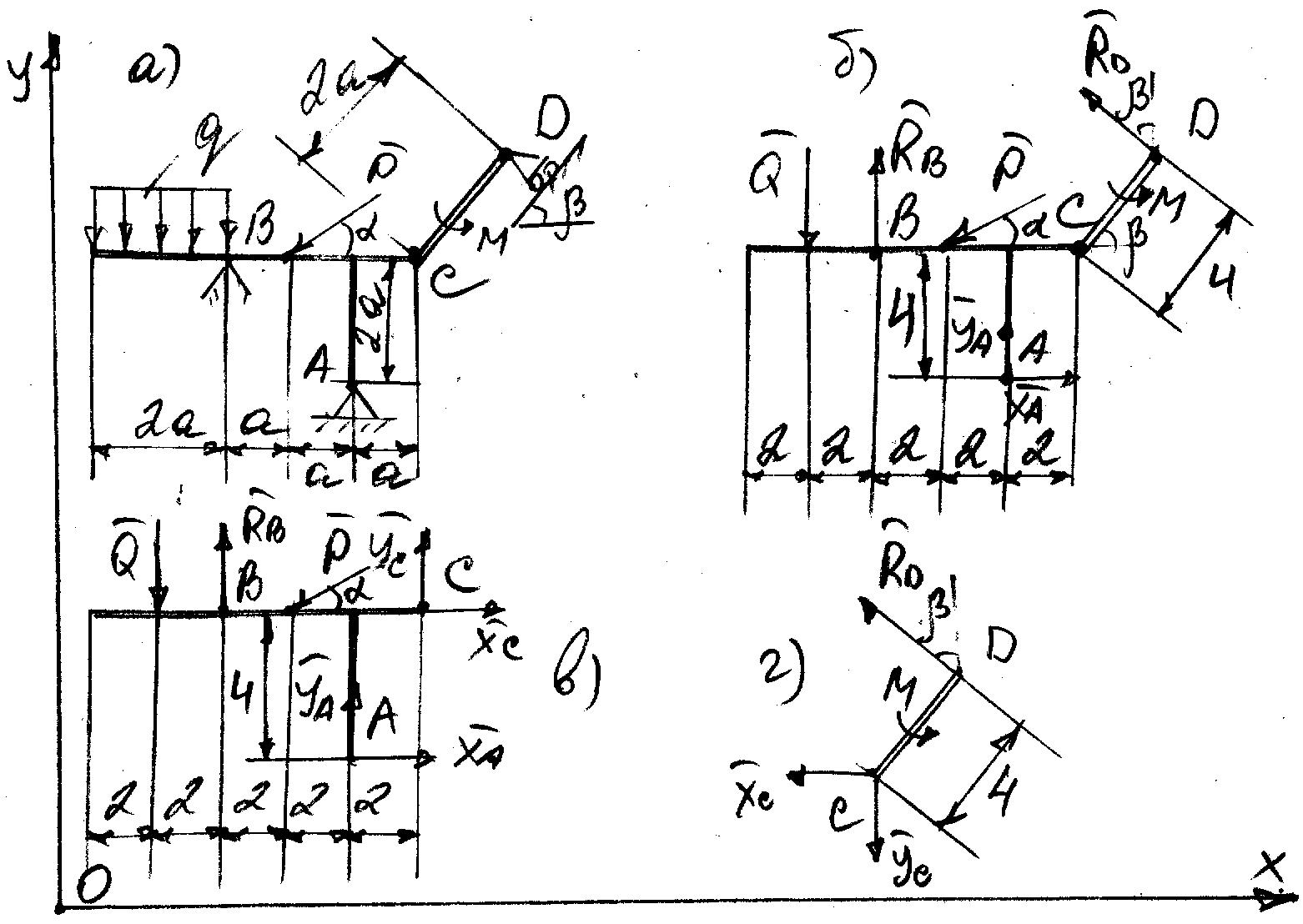 Рисунок 1.2 Рисунок 1.2Задача 1.2 Определить реакции опор составной конструкции и давление в промежуточном шарнире С. Дано: P=13kН, M=2kН*м, q=2kН/м, α= 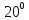 , β= , β=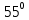 , a=2м. , a=2м.Определить: Xa,Ya, Rd, Rb, Xc, Yc-? Решение: Рассматриваем равновесие конструкции АBCD(рис.1.2,а). На конструкцию действует пара сил с моментом M, сила P и равномерно распределенная нагрузка интенсивностью q. Действие этой нагрузки заменяем равнодействующей силой Q=q*2*a=2*2*2=8кН, приложенной в середине нагруженного участка. На конструкцию действуют реактивные силы со стороны шарнира в точке А и опоры на катках в точке D, реакция стены в точке В и внутренние усилия в точке С. Показываем расчетную схему конструкции(рис.1.2,б). На конструкцию действует произвольная плоская система сил. Выбираем и показываем оси координат. Количество неизвестных реакций превышает число возможных уравнений равновесия, поэтому мы расчленяем конструкцию АBCD по шарниру С и составляем системы аналитических уравнений для каждой части: 1.Для участка АСB(рис.1.2,в): 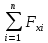 =0; Xa+Xc-P*cosα=0; =0; Xa+Xc-P*cosα=0;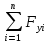 =0; Ya+Yc-Q+Rb-P*sinα=0; (1) =0; Ya+Yc-Q+Rb-P*sinα=0; (1)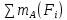 =0; Yc*2-Xc*4+Q*6-Rb*4+P*cosα*4+P*sinα*2=0; =0; Yc*2-Xc*4+Q*6-Rb*4+P*cosα*4+P*sinα*2=0;2.Для участка CD(рис.1.2,г): 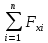 =0; -Xc-Rd*sinβ=0; =0; -Xc-Rd*sinβ=0;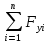 =0; -Yc+Rd*cosβ=0; (2) =0; -Yc+Rd*cosβ=0; (2)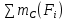 =0; Rd*4+M=0; =0; Rd*4+M=0;Вычисляем опорные реакции. Из (2): Rd=-M/4=-2/4=-0.5kH; Yc=Rd*cosβ=-0.5*0.574 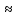 -0.287kH; -0.287kH;Xc=-Rd*sinβ=0.5*0.819 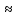 0.41kH; 0.41kH;Из (1): Rb=(Yc*2-Xc*4+Q*6+P*cosα*4+P*sinα*2)/4= =(-0.287*2-0.41*4+8*6+13*0.94*4+13*0.342*2)/4= =(-0.574-1.64+48+46.88+8.892)/4=101.558/4 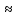 25.39kH; 25.39kH;Ya=-Yc+Q-Rb+P*sinα=-0.287+8-25.39+13*0.342= =-0.287+8-25.39+4.446 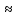 -13.23kH; -13.23kH;Xa=-Xc+P*cosα=-0.41+13*0.94=-0.41+12.22 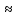 11.81kH; 11.81kH;Опорные реакции Yc, Ya, Rd получились с отрицательным знаком, следовательно, они направлены противоположно указанным на рисунке 1.2 Для проверки результатов расчета составим уравнение равновесия конструкции в виде уравнения моментов сил относительно другой точки, например B, для этого вернёмся к (рис.1.2,б) и составим уравнение моментов сил относительно точки B, при полной конструкции 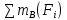 =0; Rd*sinβ*4*sinβ+Rd*cosβ*(8+4*cosβ)+M+Xa*4+Q*2+Ya*4- =0; Rd*sinβ*4*sinβ+Rd*cosβ*(8+4*cosβ)+M+Xa*4+Q*2+Ya*4--P*sinα*2=0; -0.5*4*0.671-0.5*0.574*(8+4*0.574)+2+11.81*4+8*2-13.23*4-13*0.342*2=0; -1.342-2.955+2+47.24+16-52.42-8.892=0; 65.24-65.61 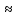 0; 0;Приблизительно, с учётом допустимой погрешности при вычислениях: 0 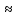 0; 0;Следовательно наше решение верное! Ответ: Xa 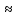 11.81kH, Ya 11.81kH, Ya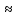 -13.23kH, Rd=-0.5kH, Rb -13.23kH, Rd=-0.5kH, Rb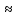 25.39H, Xc 25.39H, Xc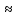 0.41kH, 0.41kH,Yc 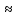 -0.287kH. -0.287kH. |
