эмм. Задача 204-1. Задача 204
 Скачать 26.74 Kb. Скачать 26.74 Kb.
|
|
Задача №204 Район порта имеет четыре причала, на которых перерабатываются четыре грузопотока генеральных грузов различных направлений (Qj) в количествах 50, 100, 40, и 60 тыс. т соответственно. Груз каждого направления перевозится определенным типом судов, а для каждого причала в процессе переработки грузов характерна определенная технология. Бюджет времени работы причалов составляет 88 суток. Производительность каждого причала при переработке определенного вида грузов и комплексные (по флоту и порту) суточные расходы по переработке грузов всех направлений на всех причалах приведены в табл. 1. Найти оптимальное закрепление причалов за грузопотоками, обеспечив минимум комплексных расходов. Таблица 1
Производительность причалов. Комплексные расходы
Решение Построим математическую модель задачи. Обозначим хij – время работы i-го причала на переработке j-го грузопотока в течение суток. Целевая функция, минимизирующая комплексные расходы: Z = 8х11 + 5х12 + 6х13 + 7х14 + 23х21 + 15х22 + 22х23 + 19х24 + 8х31 + 18х32 + 8х33 + 10х34 + 12х41 + 10х42 + 10х43 + 15х44 min. Система ограничений состоит из двух групп. Первая группа – ограничения по бюджету времени причалов: х11 + х12 + х13 + х14 88; х21 + х22 + х23 + х24 88; х31 + x32 + х33 + х34 88; х41 + х42 + х43 + х44 88 Вторая группа – ограничения по количеству перерабатываемого груза: 0,5 х11 + 2,2 х21 + 0,8 х31 + 1,2 х41 = 50; 0,6 х12 + 2,0 х22 + 0,6 х32 +1,5 х42 = 100; 0,9 х13 + 1,9 х23 + 1,0 х33 +1,5 х43 = 40; 1,0 х11 + 1,8 х21 + 0,4 х31 +1,1 х44 = 60. Требование неотрицательности: xij 0 (i = 1,2,3,4; j = 1, 2, 3, 4). Запишем данные задачи в таблицу 2, где в левом нижнем углу каждой клетки расположена производительность каждого причала при переработке определенного типа груза pij, а комплексные суточные расходы сij – в правом верхнем углу. Таблица 2
Далее работаем по алгоритму.
S1 = 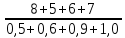 = 8,7; = 8,7;S2 = 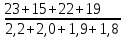 = 10; = 10;S3 = 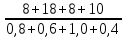 = 15,7; = 15,7;S4 = 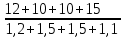 = 8,9. = 8,9.Полученные значения запишем в расчетную таблицу 3. Таблица 3
Max {8,7; 10,0; 15,7; 8,9} = 15,7
S31 = 8,0/0,8 = 10; S32 = 18/0,6 = 30; S33 = 8/1,0 = 8; S34 = 10/0,4 = 25. Полученные значения также запишем в расчетную таблицу 4. Таблица 4
11 = 100,5–8= - 3; 21 = 102,2–23= -1; 31 = 100,8–8= 0; 41 = 101,2–12= 0; 12 = 300,6–5= 13; 22 = 302–15= 45; 32 = 300,6–18= 0; 42 = 301,5-10= 35; 13 = 8,00,9–6 = 1,2; 23 = 8,01,9–22 = -6,8; 33 = 8,01,0–8 =0; 43 =8,01,5–10= 2; 14 = 251,0–7= 18; 24 = 251,8–19=26; 34 = 250,4 – 10 = 0; 44 = 251,1–15= 12,5; Значения ij запишем в левом верхнем углу каждой клетки таблица 5. Таблица 5
Положительное значение оценки характеризует суточный размер экономии расходов от переработки каждого вида груза на данном причале по сравнению с базовым вариантом, т. е. с третьим причалом. Отрицательное значение оценки характеризует суточные убытки по сравнению с базовым вариантом. 4. Наибольшее значение оценки 22 = 45 находится в клетке (2,2). С этой клетки начнем составление плана закрепления грузопотоков за причалами: х22 = min 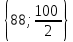 = 50. = 50.Значит, второй грузопоток второй причал перерабатывает полностью, и остается еще время 88 – 50 = 38 суток, в течение которого на данном причале могут перерабатываться другие грузы. В оставшейся части таблицы 5 (за исключением второго столбца) найдем клетку с наибольшей оценкой. Это клетка (2,4). 24 = 26 Определяем время работы второго причала по переработке четвертого грузопотока (часть бюджетного времени второго причала уже истрачено на переработку второго грузопотока, осталось 38 суток), т. е. Х24 = min 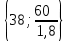 = 33,3. = 33,3.Значит, на втором причале в оставшееся время четвертый грузопоток перерабатывается не полностью, остается еще остаток грузопотока в количестве Q3 = 60 – 33,3 1,8= 0,06 тыс. т, который необходимо переработать на других причалах. В оставшейся части таблицы 5 (за исключением второго столбца, а также второй строки) найдем клетку с наибольшей оценкой. 14 = 18 Это клетка (1,4). Определяем время работы первого причала по переработке четвёртого грузопотока, т. е. Х14 = min 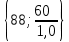 = 60. = 60.Значит, на первом причале четвертый грузопоток перерабатывается полностью, остается еще время 88 – 60= 28 суток, в течение которого на данном причале могут перерабатываться другие грузы. В оставшейся части таблицы 5 (за исключением второго и четвертого столбца, а также второй строки) найдем клетку с наибольшей оценкой. Это клетка (4,3). 43 = 2,0. Определяем время работы четвертого причала по переработке третьего грузопотока, т. е. Х43 = min 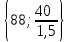 = 26,7 = 26,7Значит, третий грузопоток четвертый причал перерабатывает полностью, и остается еще время 88 – 26,7 = 61,3 суток, в течение которого на данном причале могут перерабатываться другие грузы. В оставшейся части таблицы 5 (за исключением второго и четвертого столбца, а также второй строки) найдем клетку с наибольшей оценкой. = 1,2. Это клетка (1,3). Определяем время работы первого причала по переработке третьего грузопотока (часть бюджетного времени первого причала уже истрачено на переработку четвертого грузопотока, осталось 28 суток), т. е. Х13= min 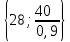 = 28 = 28Значит, на первом причале в оставшееся время третий грузопоток перерабатывается не полностью, остается еще остаток грузопотока в количестве Q3 = 40 – 28 0,9= 14,8 тыс. т, показывает, что на первом причале можно еще переработать 14,8 тыс.т. В оставшейся части таблицы 5 (за исключением второго, третьего и четвертого столбца, а также второй строки) найдем клетку с наибольшей оценкой. = 0. Это клетка (4,1). Определяем время работы четвертого причала по переработке первого грузопотока (часть бюджетного времени четвертого причала уже истрачено на переработку третьего грузопотока, осталось 61,3 суток), т. е. Х41= min 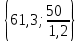 = 41,7. = 41,7.Значит, на четвертом причале в оставшееся время первый грузопоток перерабатывается не полностью, остается еще остаток грузопотока в количестве Q3 = 50 – 41,7 1,2= -0,04 тыс. т, показывает, что на четвертом причале можно еще переработать 0,04 тыс.т. В оставшейся части таблицы 5 (за исключением второго, третьего и четвертого столбца, а также второй строки) найдем клетку с наибольшей оценкой. Это клетка (3,1). 31 = 0. Определяем время работы четвертого причала по переработке третьего грузопотока, т. е. Х31 = min 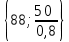 = 62,5 = 62,5Значит, первый грузопоток третий причал перерабатывает полностью, и остается еще время 88 – 62,5 = 25,5 суток, в течение которого на данном причале могут перерабатываться другие грузы. Полученные расчеты занесем в таблицу (хij записываются в центре клеток таблицы). Получим таблицу 6. Таблица 6
Полученный в таблице 6 план достаточно близок к оптимальному. Он обеспечивает переработку всех грузопотоков при расходах: Z = 6 28 + 7 60 + 15 50 + 19 33,3 + 8 25,5 + 1241,7+ 10 26,7 = 2942,1 тыс. руб. и остатке неиспользованного времени второго, третьего и четвертого причалов (4,7; 62,5 и 19,6 суток). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
