Вариант 2. Задача 3 Ответ 1 0,63 2 0,97 Объяснение Р0,9 вероятность попасть в цель для первого стрелка
 Скачать 121.58 Kb. Скачать 121.58 Kb.
|
|
Вариант 2  Задача 3 Ответ: 1) 0,63; 2) 0,97 Объяснение: Р₁=0,9 - вероятность попасть в цель для первого стрелка Р₂=0,7 - вероятность попасть в цель для второго стрелка 1) Событие А - оба стрелка попали в цель Применим теорему об умножении вероятностей, получим Р(А)= Р₁*Р₂ =0,9*0,7 = 0,63 2) Событие В - хотя бы один стрелок попадёт в цель Событие С - оба стрелка промахнутся Вероятность Р(С) промаха у обоих стрелков (по теореме об умножении вероятностей) равна Р(С) = (1-Р₁)(1-Р₂)=(1-0,9)(1-0,7)= 0,1*0,3 = 0,03 Событие В - это событие, противоположное событию С, значит, Р(В) = 1 - Р(С) = 1-0,03 = 0.97 Задача 4 Р 10,3 = С 310 = (1/5)3 (4/5)7 = 0,201 Задача 6 Решение F (x)= 2x1+3x2 Х = (Х1, Х2) Расход исходного продукта для производства обоих видов изделий ≤ Максимально возможный запас данного исходного продукта 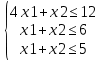 х1, х2 0. Общая прибыль от реализации х1 изделий вида А и х2 изделий вида В составит F = 2х1 + 1х2. Таким образом, приходим к следующей математической задаче: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение. 1) 4х1 + х2 = 12 х2 = 12 - 3х1 2) х1 + х2 = 6 х2 = 6 - х1 3) х1 + х2 = 5 х2 = 5 - х1 |
