Эконометрика. Задача 33. В таблице дано распределение 134 стран по уровню относительных цен х (в к ценам сша) и ввп на душу населения y (тыс долл в ценах 1993 г.). ух
 Скачать 168.06 Kb. Скачать 168.06 Kb.
|
|
Задача 33. В таблице дано распределение 134 стран по уровню относительных цен Х (в % к ценам США) и ВВП на душу населения Y (тыс. долл. в ценах 1993 г.).
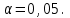 Требуется: В прямоугольной системе координат построить эмпирические ломаные регрессии U на C и C на U, сделать предположение о виде корреляционной связи. Оценить тесноту линейной корреляционной связи. Составить линейные уравнения регрессии U на C и C на U, построить их графики в одной системе координат. Дать экономическую интерпретацию полученных результатов. Выполнить решение данной задачи средствами Excel Проверить гипотезу о значимости коэффициента корреляции при уровне значимости a. Выполнить прогноз переменной У при условии, что переменная Х увеличится на 15% по сравнению с последним наблюдением. Решение 1. В корреляционной таблице даны интервальные распределения, поэтому за значения вариант нужно брать середины частичных интервалов.
При Х = 10 признак Y имеет распределение
Условное среднее 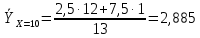 При Х = 30 признак Y имеет распределение
Условное среднее 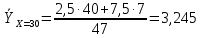 При Х = 50 признак Y имеет распределение
Условное среднее 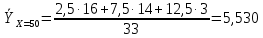 При Х = 70 признак Y имеет распределение
Условное среднее 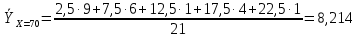 При Х = 90 признак Y имеет распределение
Условное среднее 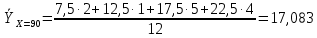 При Х = 110 признак Y имеет распределение
Условное среднее 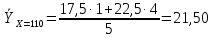 При Х = 130 признак Y имеет распределение
Условное среднее 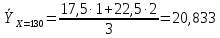 Получаем таблицу, выражающую корреляционную зависимость 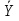 от X от X
Аналогично вычисляются условные средние 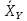 Y = 2,5
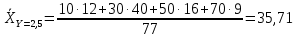 Y = 7,5
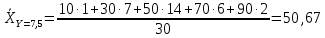 Y = 12,5
 Y = 17,5
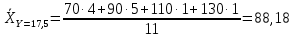 Y = 22,5
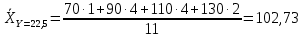 Таблица, выражающая корреляционную зависимость 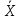 от Y от Y
В прямоугольной системе координат: отображаем точки 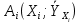 , соединяем их отрезками прямых; получается эмпирическая линия регрессии Y на X. , соединяем их отрезками прямых; получается эмпирическая линия регрессии Y на X.отображаем точки 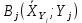 , соединяем их отрезками прямых; получается эмпирическая линия регрессии X на Y. , соединяем их отрезками прямых; получается эмпирическая линия регрессии X на Y.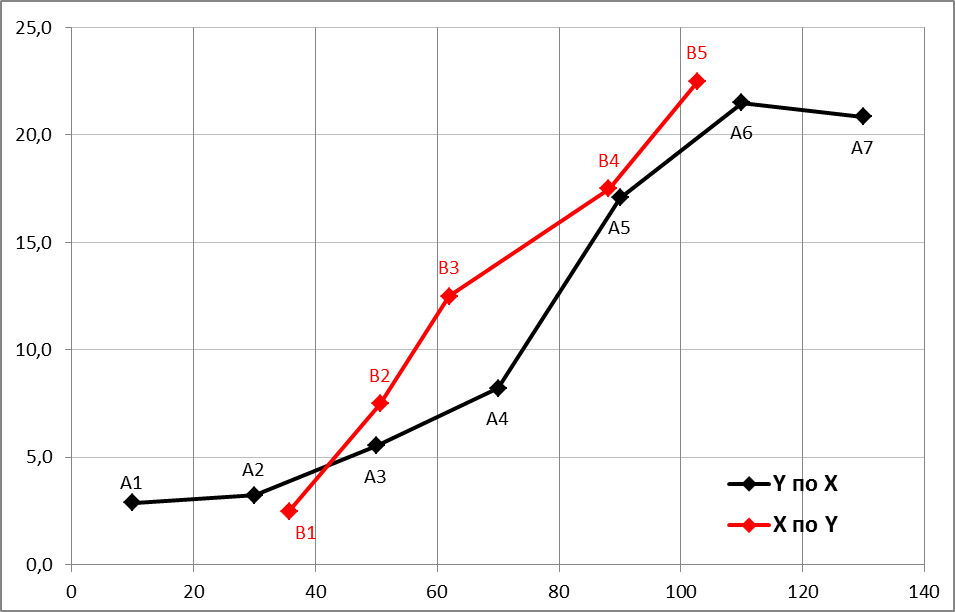 Выдвигаем гипотезу о линейной корреляционной зависимости между X и Y. 2. Оценка тесноты линейной корреляционной связи Нужно вычислить выборочный коэффициент корреляции. 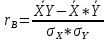 Расчеты проведены с помощью MS Excel 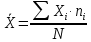 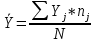 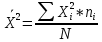 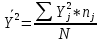  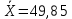 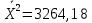  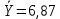 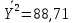 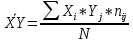 Произведения 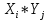  Частоты 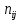  Пользуемся функцией СУММПРОИЗВ: перемножается таблица парных произведений 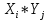 и таблица частот а затем делится на N = 134. и таблица частот а затем делится на N = 134.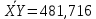 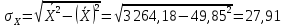 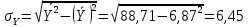 Выборочный коэффициент корреляции 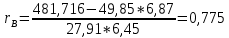 Величина выборочного коэффициента корреляции 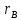 показывает, что корреляционная связь между Y и X высокая. показывает, что корреляционная связь между Y и X высокая.3. Линейные уравнения регрессии Уравнение регрессии Y на X 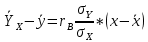 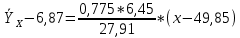 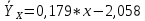 Уравнение регрессии X на Y 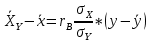 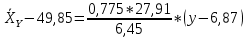 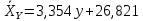 Изображаем графики прямых линий регрессии на чертеже  4. Экономическая интерпретация полученных результатов. 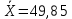 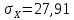 Средний уровень относительных цен в % к ценам США составляет 49,85% со средним отклонением 27,91%. 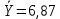 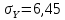 Средний уровень ВВП на душу составляет 6,87 тыс. долл со средним отклонением 6,45 тыс. долл. Уравнение Y на X 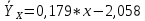 При увеличении X (относительных цен в % к ценам США) на 1 единицу, ВВП на душу населения Y увеличивается в среднем на 0,179 тыс. долл. Уравнение X на Y 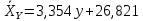 При увеличении Y (ВВП на душу населения) на 1 тыс. долл., относительные цены повышаются на 3,354% в среднем. 5. Решение задачи в Excel Команда Данные-Анализ данных – Регрессия По данным корреляционной таблицы составляем ряд значений. В корреляционной таблице заданы частоты появления в наблюдении пары значений (xi,yj). Их все записываем в один ряд, каждая пара повторяется с заданной частотой. Всего будет N = 134 наблюдения  Уравнение YX=0,179∗x−2,058YX=0,179∗x−2,058 График уравнения 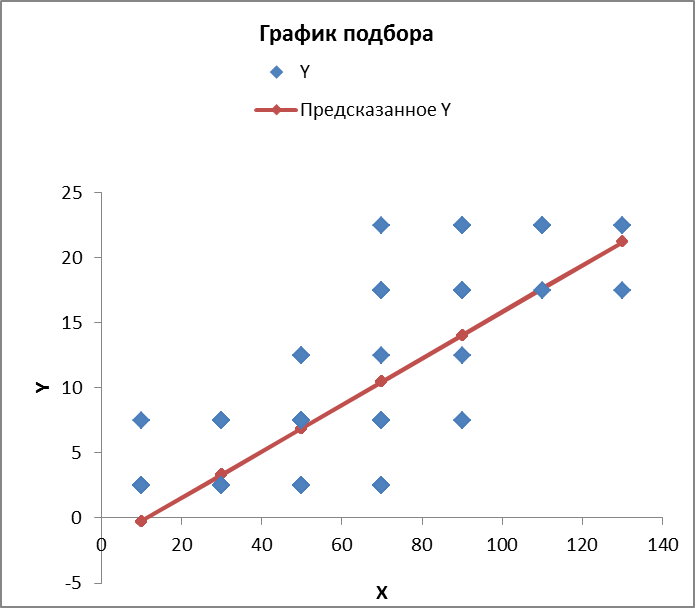 Уравнение XY=3,354y+26,821XY=3,354y+26,821 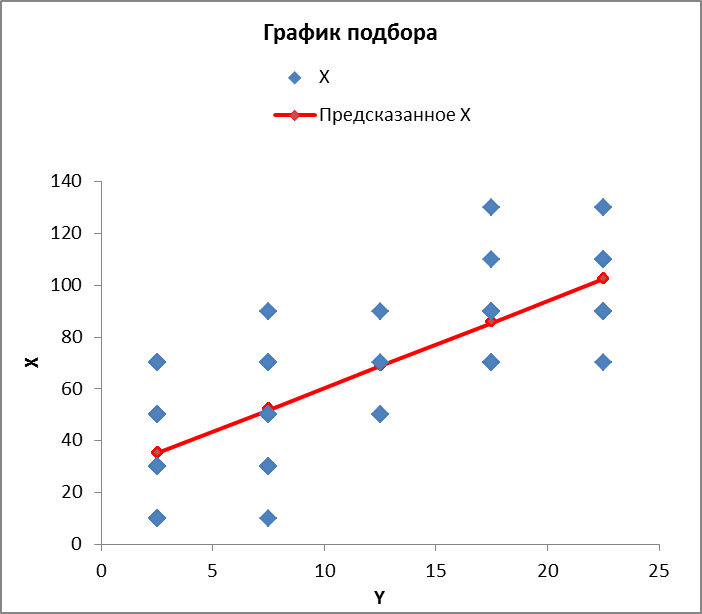 Решение задачи в Excel Добавление линии тренда Вывод: Коэффициент корреляции, рассчитанный вручную (0,775) совпал с рассчитанным с помощью команды Анализ данных – Регрессия (в результатах Множественный R). Коэффициенты уравнений регрессий, найденные вручную тоже совпали с коэффициентами, выведены Excel в результатах анализа. Также построены линии тренда Y по X и X по Y с помощью команды Добавить линию тренда на диаграмме. Уравнения этих линий такие же. |