контрольная работа вар 4. Задача 411. Колесо радиусом 5 см вращается так, что зависимость угла поворота радиуса колеса от времени дается формулой
 Скачать 126.54 Kb.
|
|
Контрольная работа 1. Задача 411. Колесо радиусом 5 см вращается так, что зависимость угла поворота радиуса колеса от времени дается формулой φ = A+Bt+Ct2+Dt3, где А=3 рад, В=2 рад /с, С=1 рад/ с2, D=l рад/с3. Найти изменение тангенциального ускорения для точек на ободе колеса за каждую секунду движения Дано: R = 5 см = 0,05м Δt = 1c φ=A+Bt+Ct2+Dt3 D = 1 рад/с3 Найти: ∆aτ - ? Решение. Угловое ускорение является второй производной от угла поворота от времени  Проверим единицы измерения 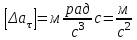 Ответ.  Задача 412. С вершины наклонной плоскости начинает скользить тело без начальной скорости. Угол наклона плоскости к горизонту 30°, а её длина равна 12 м. Коэффициент трения 0,15. Сколько времени продолжается движение тела по наклонной плоскости ? Дано: v0 = 0 l = 12 м α = 300 μ = 0,15 Найти: t - ? Решение. 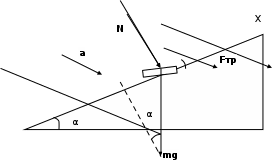 Y Cпроектируем второй закон Ньютона на выбранную систему координат  Проверим единицы измерения 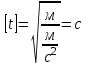 Ответ.  Задача 413. На барабан радиусом 0.2 м намотан шнур, к которому подвешен груз массой 0.5 кг. До начала вращения барабана высота груза над полом равна 1 м. Через сколько времени груз опустится до пола? Момент инерции барабана равен 0.1 кгм2. У меня 2b, здесь без изменений Дано: R = 0.2 м m = 0.5 кг h = 1 м I = 0.1 кгм2 v0 = 0 Найти: t - ? Р  ешение.Изобразим заданную систему на рисунке. Обозначим угол поворота барабана как , а его скорость – как . Угловая скорость барабана – это производная его угловой координаты:  . (1)Угловое ускорение барабана – это производная его угловой скорости:  . (2)На барабан действует постоянный момент М. Величина этого момента равна:  , (3)где T – сила натяжения нити. Обозначим ускорение груза как а. Это ускорение связано с угловым ускорением вращения барабана следующим соотношением:  (4)На груз действуют сила тяжести и сила натяжения нити (см. рисунок). Силу натяжения нити находим из уравнения движения груза, учитывая соотношение (4):   , (5)где  – ускорение свободного падения.Тогда дифференциальное уравнение, описывающее вращение барабана под действием приложенного к нему постоянного моментом M, выглядит так: 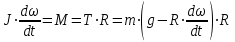   . (6)В момент начала вращения начальная скорость вращения барабана 0 равна 0. Поэтому, интегрируя (5), получим следующее уравнение:   . (7)Откуда зависимость угловой скорости барабана от времени выглядит:  . (8)Подставляем (8) в (1), интегрируем получившееся уравнение и находим закон изменения угла поворота барабана, приняв за начальный угол нулевой:   . (9)Находим время, за которое груз опустится на расстояние h, а барабан повернётся на соответствующий угол  :  .Поверка размерностей:  .Задача 414. Медный шар радиусом 10 см вращается вокруг оси, проходящей через его центр, совершая 2 об/с. Какую работу надо совершить, чтобы увеличить скорость вращения вдвое ? Дано: r = 0,1м n1 = 2об/с n2 = 2n1 ρ = 8,6∙103кг/м3 Найти: A - ? Решение. По закону сохранения энергии работа будет равняться изменению кинетической энергии шара  Проверим единицы измерения  Ответ.  Задача 415. Амплитуда гармонических колебаний материальной точки равна 5см, масса точки 10 г, а полная энергия колебаний равна 9,1·10-5 Дж. Написать уравнение этих гармонических колебаний, если начальная фаза колебаний равна 60°. Дано: xm = 0,05м m = 0,01кг W = 9,1·10-5 Дж φ0 = 60°= π/3 Найти: x(t) - ? Решение. Пусть колебания происходят по закону синусов, т.е. 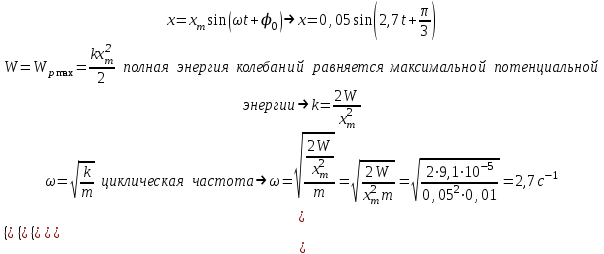 Ответ.  Задача 416 В баллоне вместимостью V= 25 л находится водород при температуре Т = 290 К . После того как часть водорода израсходовали, давление в баллоне понизилось на Δр = 0.4 МПа. Определить массу m израсходованного водорода. Дано:  Найти:  Решение: Уравнение состояния идеального газа имеет вид: 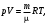 где R = 8.31 Дж/(моль∙К) – универсальная газовая постоянная.Для начального и конечного состояний можем записать:  где  - молярная масса водорода.Решая систему, получаем:  Ответ: = 8.3 г.Задача 417 Средняя квадратичная скорость молекул некоторого газа равна 450 м/с. Давление газа равно 5·104 Па. Найти плотность газа при этих условиях. Дано:  Найти:  Решение: Плотность газа равна  где m – масса газа, V – его объем.Уравнение состояния идеального газа имеет вид: 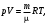где R = 8.31 Дж/(моль∙К) – универсальная газовая постоянная.Следовательно,  Средняя квадратичная скорость молекул равна 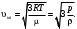 Отсюда  Ответ: 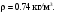 Задача 418 2·10-3 м³ азота находятся под давлением 105 Па. Какое количество тепла надо сообщить азоту, чтобы при постоянном давлении увеличить его объем вдвое ? Дано: 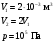 Найти: Q Решение: Работа расширения газа в изобарическом процессе равна  Приращение внутренней энергии газа равно  Для азота (двухатомный газ) число степеней свободы молекулы i = 5. Соответственно,  Согласно первому началу термодинамики  Ответ: Q = 700 Дж. |