Навигация по странице:Найти
|
Техническая механика. Задача 5 a дано q 1 2q q 2 q m 1 3m m 2 m p 1 p p 2 P
ЗАДАЧА № 5
A) Дано:
q1 = 2q
q2 = q
m1 = 3m
m2 = m
P1 = P
P2 = P
Найти:
Q1-4 = ?
Мк1-4 = ?
Построить эпюры
|
|
Решение:
1)
|
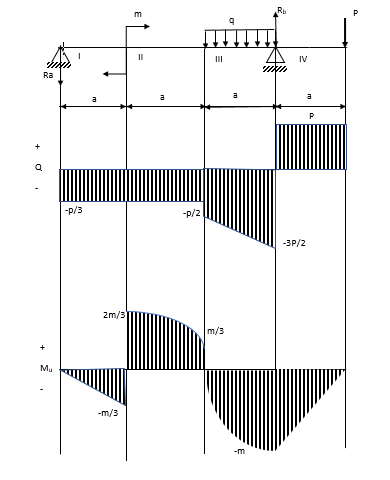
Кроме перечисленных сил, на балку действуют еще две реактивные силы RA и RB. Определим их значение, составив уравнения моментов:
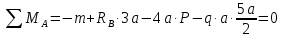
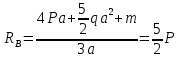
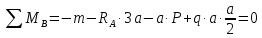
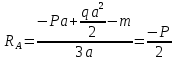
Одна реактивная сила оказалась отрицательной, значит ее направление не соответствует предварительно выбранной, другая реактивная сила положительная, а соответственно соответствует предварительно выбранной (на рисунке изображены уже измененные направления реактивных сил).
Т.к. известны значения всех сил, приложенных к балке, то расчет любого участка можно выполнять как слева направо, так и справа налево. Можно менять направление расчета в пределах решения одной задачи.
|
2)
|
Рассчитаем эпюру Q:
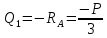
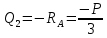
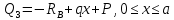
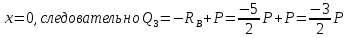
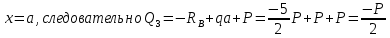
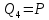
|
3)
|
Рассчитаем эпюру Mu:
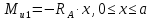
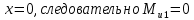
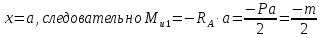
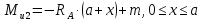
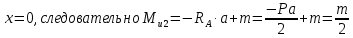
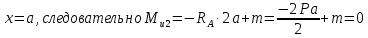
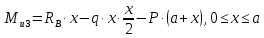

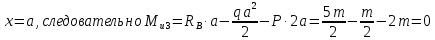
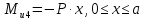
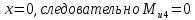
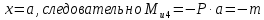
Построим эпюры Q и Mu
|
Б) Дано:
q1 = 2q
q2 = q
m1 = 3m
m2 = m
P1 = P
P2 = P
Найти:
Q1-3 = ?
Мк1-3 = ?
Построить эпюры
|
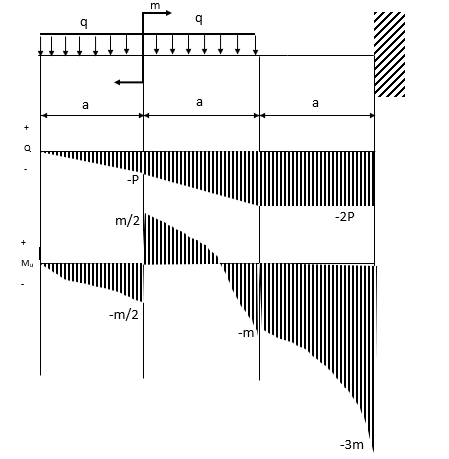
|
Решение:
1)
|
При расчете жестко заделанных балок реактивные силы не определяют. Расчет ведем от свободного конца в сторону заделки.
|
2)
|
Рассчитаем эпюру Q:
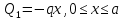
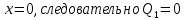
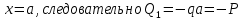
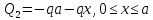
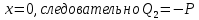
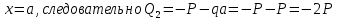
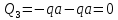
|
3)
|
Рассчитаем эпюру Mu:
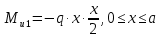
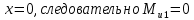
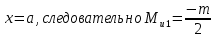
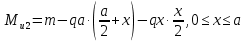
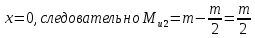
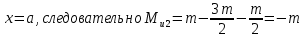
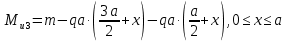
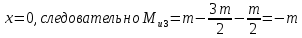
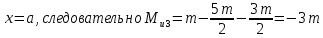
Построим эпюры Q и Mu
|
Задача № 6
Дано:
q = 10 кН/м
P = 10 кН
m = 10 кН
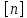 = 2 = 2
a = 1 м
Сталь 30
q1 = 2q
q2 = q
P1 = 3P
P2 = P
m1 = 2m
m2 = m
σт = 300 МПа
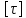 = 80 МПа = 80 МПа
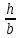 = 2 = 2
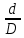 = 0,8 = 0,8
Найти:
Q1-3 = ?
Мк1-3 = ?
Рассмотреть формы поперечных сечений
|
|
Решение:
1)
|
Составим уравнение равновесия и решим вопрос о статической определимости бруса:
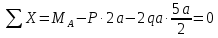
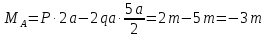
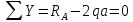
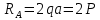
|
2)
|
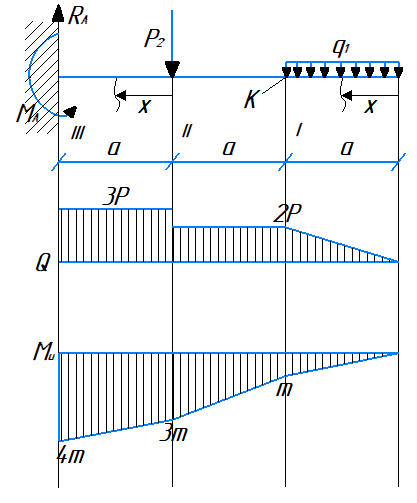
Построим эпюры поперечных сечений Q и изгибающих моментов Mu:
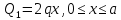
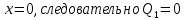
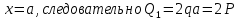
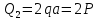
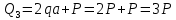
|
3)
|
Построим эпюры изгибающих моментов Mu:
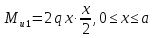
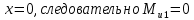
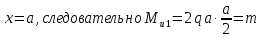
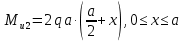

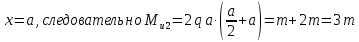
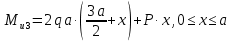
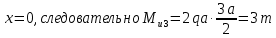
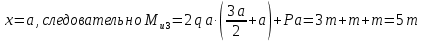
Опасным является сечение в заделке, т.к. момент в этом сечении по модулю максимален.
|
4)
|
Из условия прочности балки по нормальным напряжениям определяем требуемое значение осевого момента сопротивления в опасном сечении:
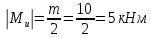
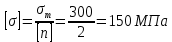
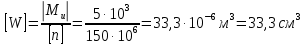
|
5)
|
Определяем размеры сечений:
Прямоугольное сечение. Уточняем формулу для определения осевого момента сопротивления прямоугольного сечения с учетом соотношения сторон (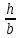 = 2) и приравниваем к требуемому значению: = 2) и приравниваем к требуемому значению:
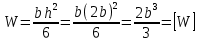
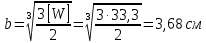
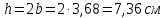
Круглое сечение. Формулу для определения осевого момента сопротивления круглого сечения приравниваем к требуемому значению:
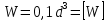
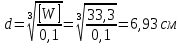
Кольцевое сечение. Уточняем формулу для определения осевого момента сопротивления кольцевого сечения с учетом соотношения диаметров (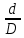 = 0,8) и приравниваем к требуемому значению: = 0,8) и приравниваем к требуемому значению:
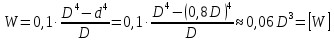
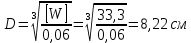
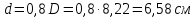
Двутавровое сечение. Для выбора двутаврового сечения используем Приложение 1. Выбираем двутавр, у которого осевой момент сопротивления Wx имеет значение наиболее близкое к требуемому [W].
Прочность двутавровой балки обеспечит двутавр №10 (Приложение 1), для которого: Wx = 39,7 см3, Ix = 198 см4, Sx = 23,0 см3, А = 12,0 см2.
|
6)
|
Решаем вопрос о рациональности форм поперечных сечений, сопоставляя площади просчитанных сечений.
Площадь прямоугольного поперечного сечения:
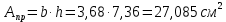
Площадь круглого поперечного сечения:
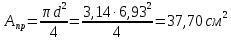
Площадь кольцевого поперечного сечения:
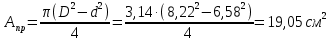
Площадь двутаврового поперечного сечения по сортаменту:
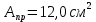
Наиболее рациональной является двутавровая балка.
|
7)
|
Проверяем прочность двутавровой балки по касательным напряжениям: Sx = 23,0 см3, Ix = 198 см4, b = 4,5 мм, Q = 20 кН.
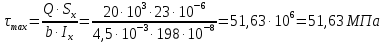
Условие прочности выполняется 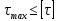
|
8)
|
Прогиб в точке К определим с помощью метода начальных параметров.
Начальные параметры: 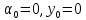
Обобщенное уравнение прогибов:
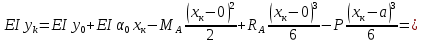
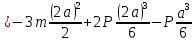
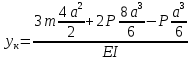
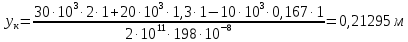
Сечение К перемещается вниз на 212,95 мм.
|
|
Ответ:
|
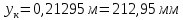
| |
|
|
 Скачать 69.96 Kb.
Скачать 69.96 Kb.