Задача сопротивления материалов. Задача №5. Задача 5 Условие задачи
 Скачать 95.43 Kb. Скачать 95.43 Kb.
|
|
Задача №5 Условие задачи. Для поперечного сечения (рис. 1) определить положение главных центральных осей и величины соответствующих главных моментов инерции. Исходные данные.
 Рис. 1. Заданная схема Дано:  ; ;  мм; мм;  мм; мм;  мм; мм;№ схемы ‒II. Решение. 1. По исходным данным вычертим поперечное сечение в масштабе 1:1. 2. Составное сечение разобьем на  простые фигуры: простые фигуры:1) прямоугольник (основная площадь) с размерами: ширина  высота  2) прямоугольник (дополнительная площадь) с размерами: ширина  высота  4) круг (дополнительная площадь) с диаметром  3. Проведем прямоугольную систему координат  . Отметим на чертеже сечения центры тяжести каждой простой фигуры C1, C2, C3. . Отметим на чертеже сечения центры тяжести каждой простой фигуры C1, C2, C3.4. Определим координаты центров тяжести (  каждой простой фигуры: каждой простой фигуры: ; ;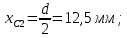   ; ;  5. Определим положение центра тяжести сечения. Площади простых фигур:    Площадь всего сечения  Координаты центра тяжести всего сечения:   6. Отметим на чертеже центр тяжести «С» сечения с координатами (  . Проведем через центры тяжести простых фигур центральные оси . Проведем через центры тяжести простых фигур центральные оси  , параллельные осям , параллельные осям  . .7. Определим моменты инерции простых фигур относительно их центральных осей. Для прямоугольника 1):    Для прямоугольника 2):    Для круга 3):    8. Определим моменты инерции простых фигур относительно центральных осей сечения. Расстояния между параллельными центральными осями:   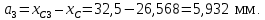    Определим моменты инерции простых фигур относительно центральных осей  и и  . .Для прямоугольника 1):    Для прямоугольника 2):    Для круга 3):    9. Определим осевые и центробежный моменты инерции всего сечения относительно его центральных осей  и и  : :   10. Определение положения главных осей инерции   11. Определим главные моменты инерции сечения. Вначале определим экстремальные значения главных центральных моментов инерции сечений: 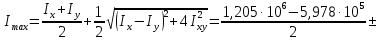  Определим, какое значение (максимальное или минимальное) будет у главного момента инерции, взятого относительно главной оси  , расположенной под углом , расположенной под углом  к центральной оси к центральной оси  . Для этого определим знак выражения . Для этого определим знак выражения 12. Выполним проверку проведенных вычислений:   |




