коробовая прямая. Задача 5 Вычисление геометрических характеристик несимметричных сечений из прокатных профилей (рисунок 5)
 Скачать 394.68 Kb. Скачать 394.68 Kb.
|
|
Задача №5: Вычисление геометрических характеристик несимметричных сечений из прокатных профилей (рисунок 5). 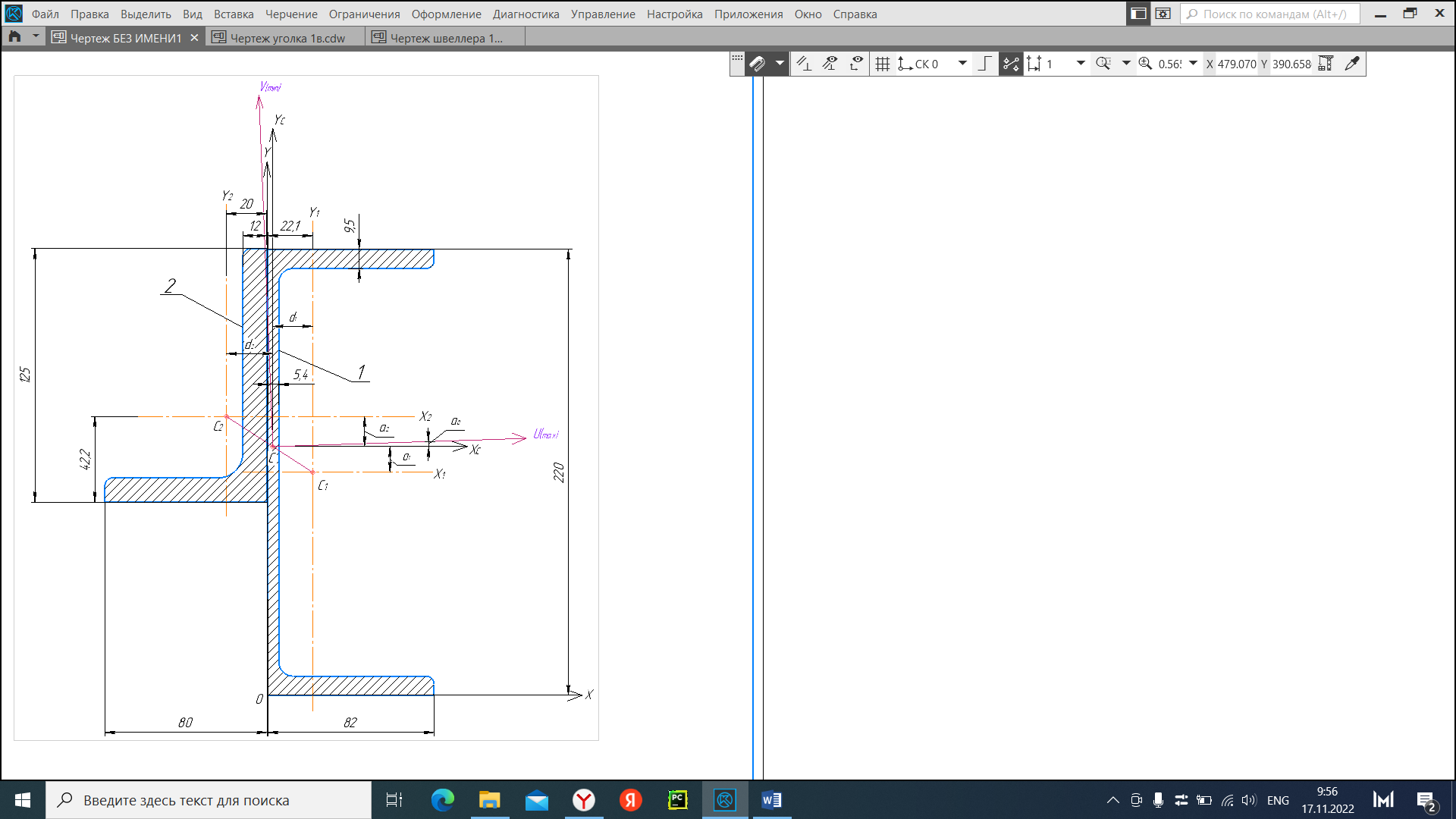 Рисунок 5 – Несимметричные сечения из прокатных профилей, положение главных осей инерции, центры тяжести фигур 1 – швеллер №22; 2 – уголок неравнополочный № 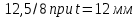 ; ;На рисунке 6 представлен швеллер №22 из ГОСТ 8240-89. 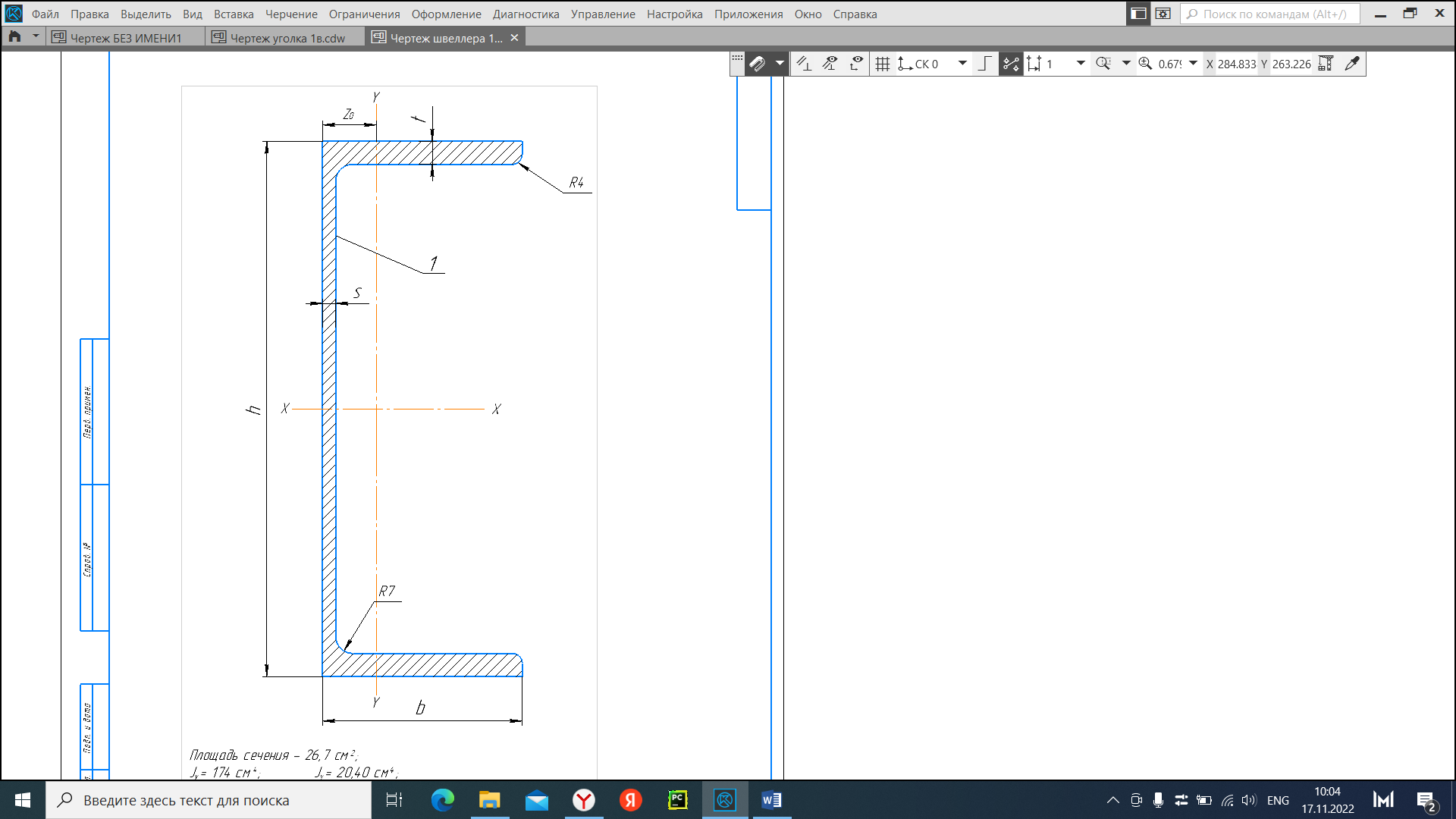 Рисунок 6 – Швеллер №22 из ГОСТ 8240-89 Данно: 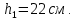 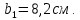 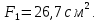 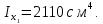 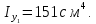 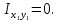 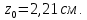 На рисунке 7 представлен уголок неравнополочный №12,5/8 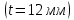 из ГОСТ 8510-89. из ГОСТ 8510-89.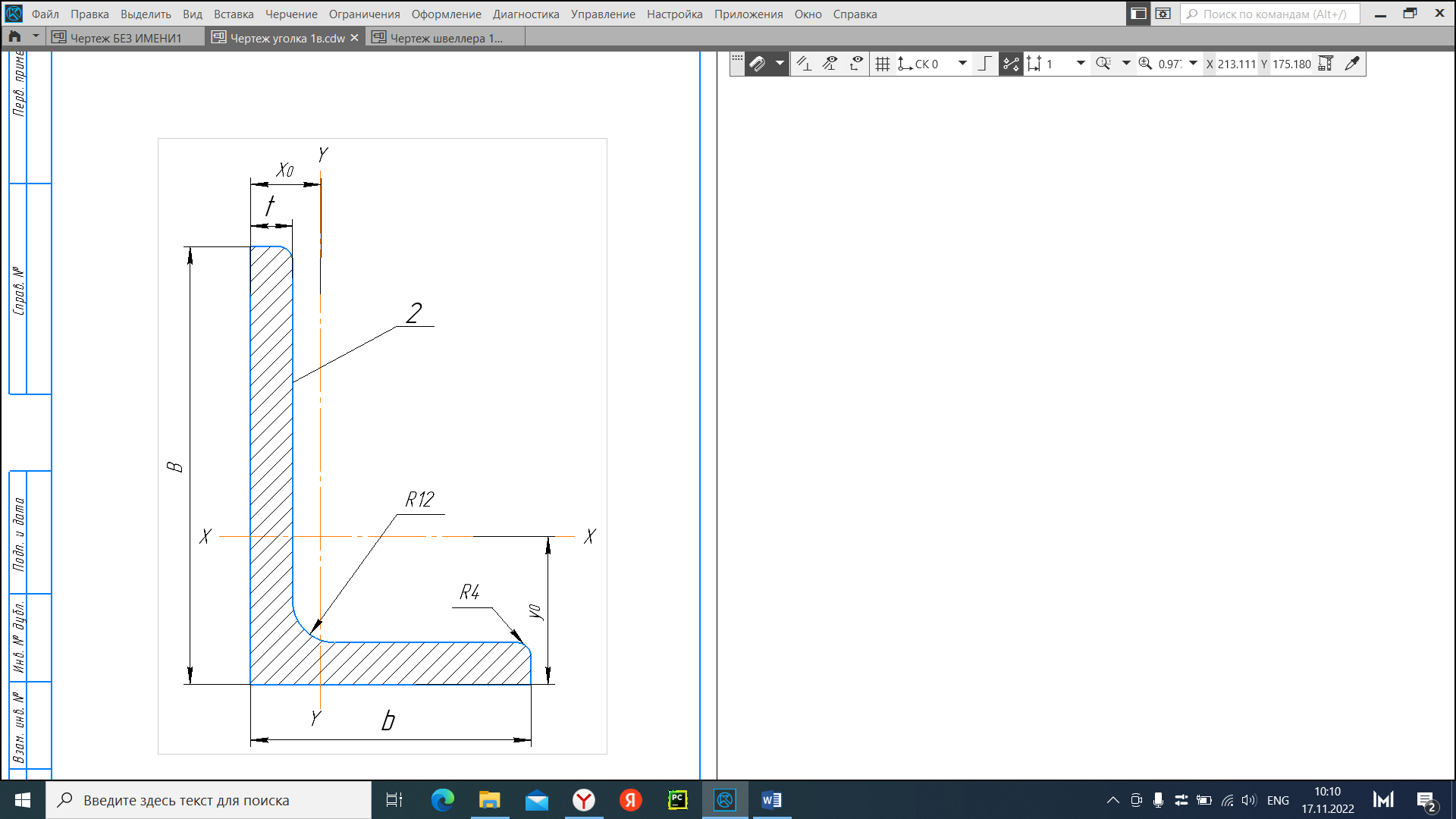 Рисунок 7 – Уголок неравнополочный №12,5/8 (t = 12мм) из ГОСТ 8510-89 Данно: 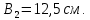 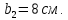 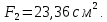 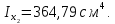 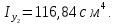 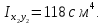 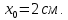 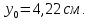 Требуется: Определить координаты центра тяжести составного сечения 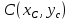 . .Определить осевые центральные моменты инерции сечения ( 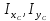 ) и центробежный момент инерции сечений ( ) и центробежный момент инерции сечений (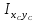 ). ).Определить положение главных осей инерции U, V. Определить главный момент инерции ( 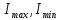 ) )Решение: Определим положение центра тяжести сечения: Выбираем вспомогательные оси YOX, находим координаты 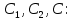 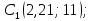 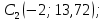 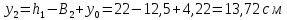 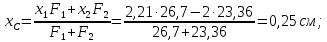 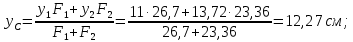 Определим осевые центральные моменты инерции сечения: 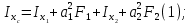 Найдем расстояние между осями С и С1: 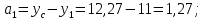 учитывая знак учитывая знак 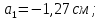 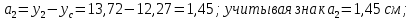 Подставим в (1) формулу: 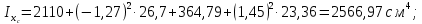 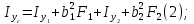 Найдем расстояние между осями С и С2: 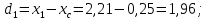 учитывая знак учитывая знак 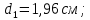 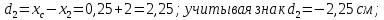 Подставим во (2) формулу: 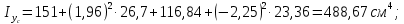 Определим центробежный момент инерции сечений: 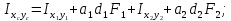 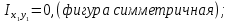 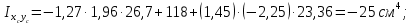 Определим положение главных осей симметрии: 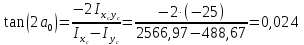 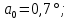 Поворот против часовой стрелки. Определим главные моменты инерции: 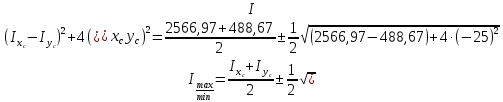 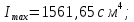 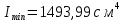 Выполним проверку: 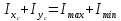 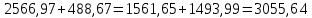 Проверка выполняется. Вывод: определено положение центра тяжести сечения С 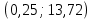 ,вычислены осевые центральные моменты инерции ,вычислены осевые центральные моменты инерции 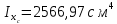 и и 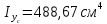 и центробежный момент инерции и центробежный момент инерции 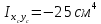 , а также определено положение главных осей инерции α0 = , а также определено положение главных осей инерции α0 = 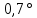 , , 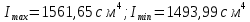 . . |
