Задача. Задача 586 стр. 155, геометрия 79, автор Атанасян Л. С
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
|
Задача №586 стр.155, геометрия 7-9, автор Атанасян Л.С. Постройте треугольник по 2 углам и биссектрисе, проведенной из вершины меньшего угла. Что дано? (2 угла и отрезок) Что требуют в задаче? (построить треугольник) Чертим в тетради 2 угла и отрезок. (Дети чертят в тетради 2 угла и отрезок.)  Итак, задача на построение. Сколько этапов и какие в задаче на построение? (Анализ) Что предполагает анализ? (На этом этапе должны быть подмечены такие зависимости между данными фигурами и искомой фигурой, которые позволили бы в дальнейшем построить эту искомую фигуру) Давайте построим треугольник по двум углам. 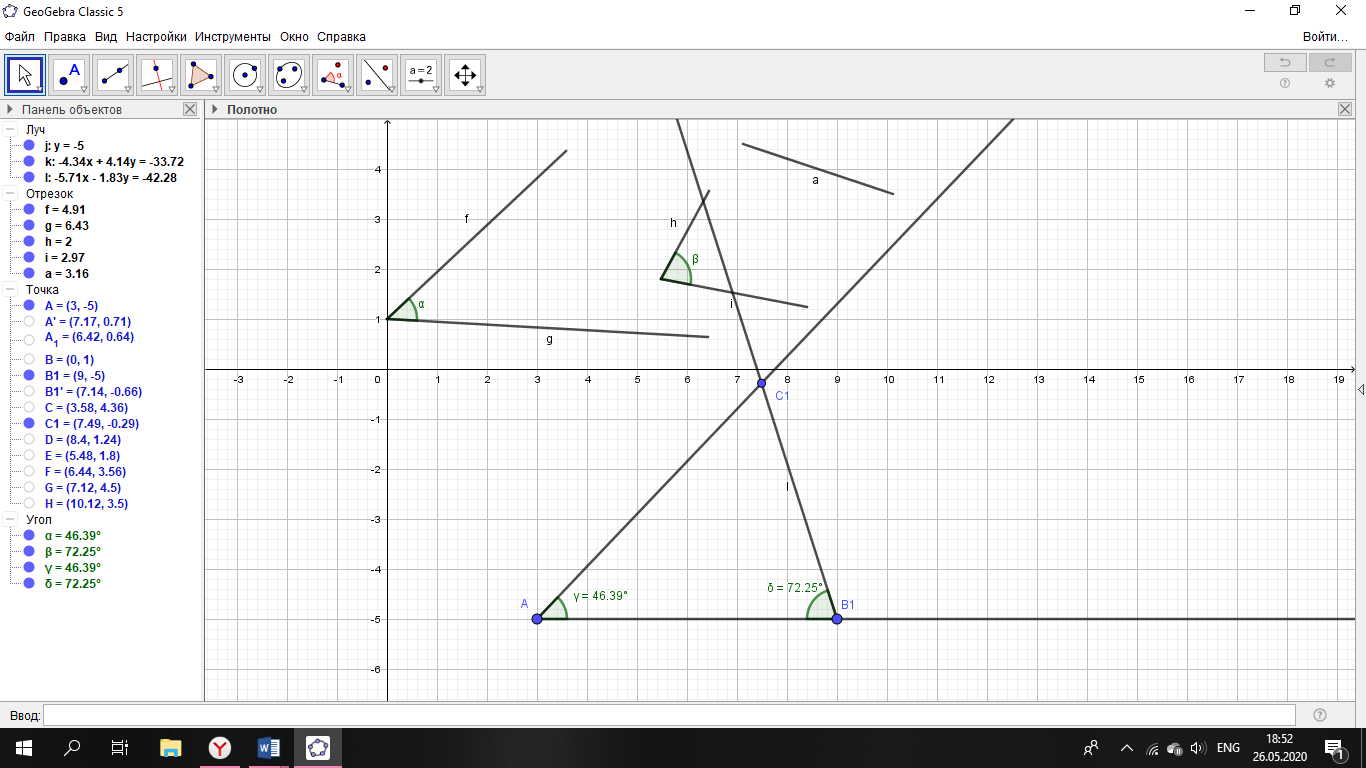 Будет этот треугольник искомым? (Нет, он подобен тому, который надо построить.) Да, одно условие мы исключили. Какое это условие? (Биссектриса меньшего угла.) Что такое биссектриса угла? (Луч, выходящий из вершины угла, который делит угол пополам) Строим биссектрису меньшего угла А. Итак, биссектриса есть, треугольник искомый? (Нет, биссектриса должна быть определенной длины.) Откладываем на биссектрисе отрезок равный данному. 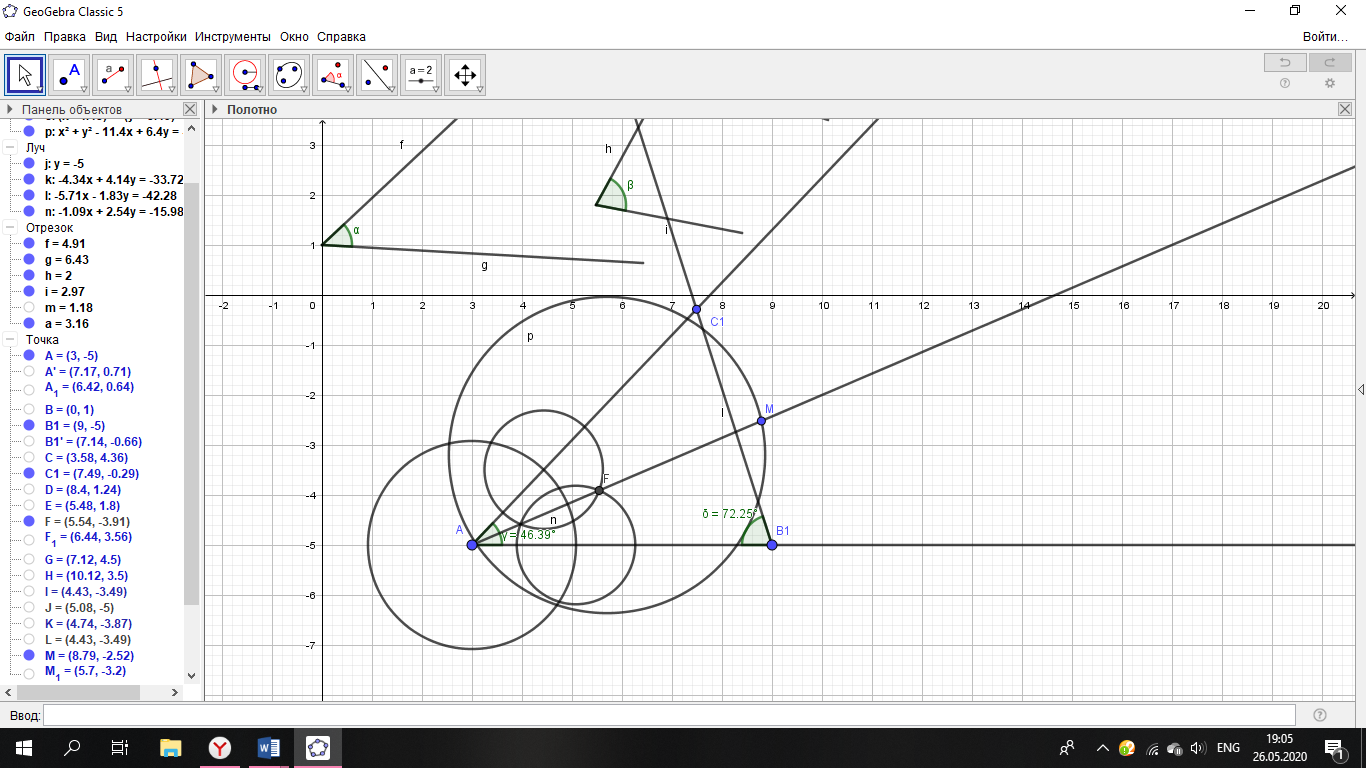 Наш треугольник должен быть подобен построенному. Что достаточно провести через т.М для завершения построения? (Прямую, параллельную В1С1) 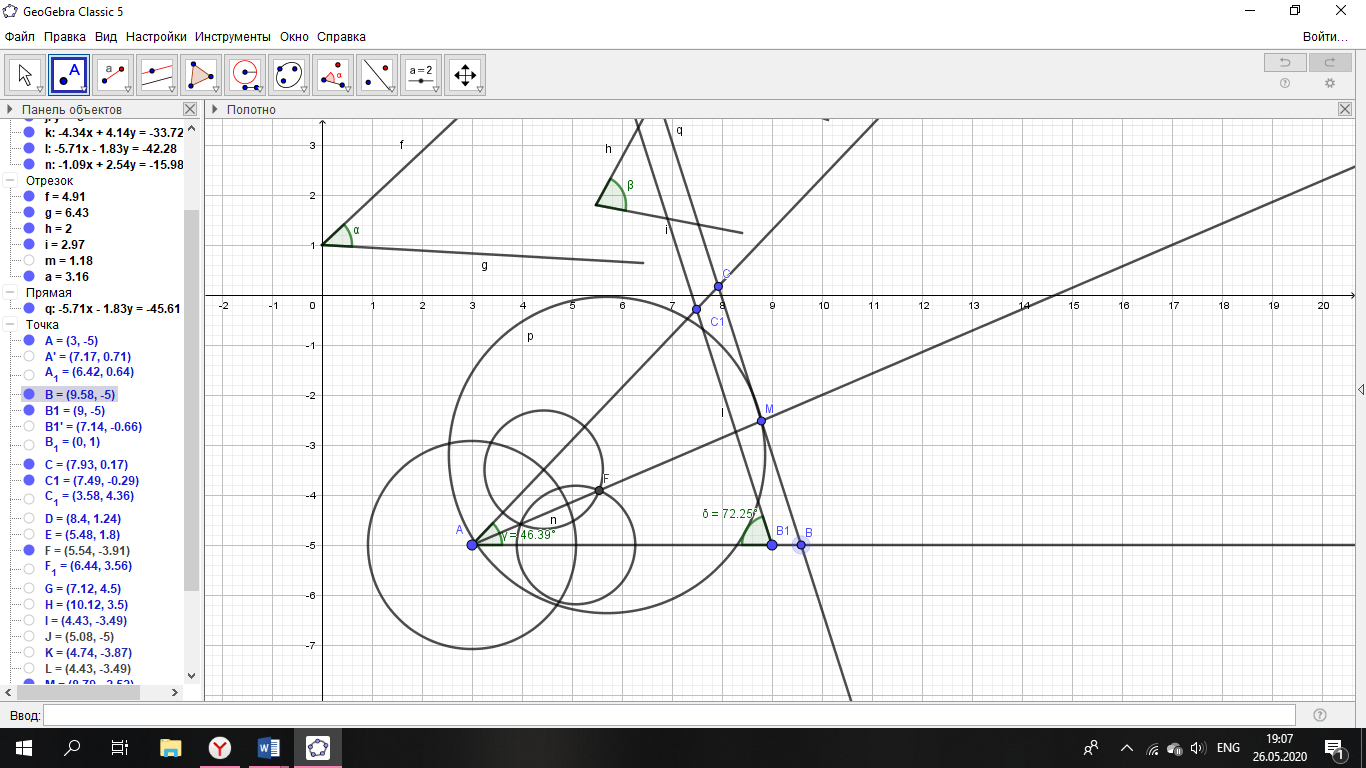 Какой следующий этап при решении задач на построение? (Построение) Один ученик выходит к доске строит и записывает основные этапы построения. Построение. 1.(а) прямая,Ає а; 2. 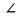 А= А= 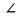 1; 1;3.В1 є а; 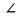 В1= В1=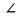 2; 2;4. 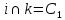 5.АК- биссектриса; 6.АM=b; 7.Mє n; n 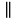 С1В1; С1В1; 8.(n) 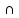 АС1=С; АС1=С;(n) 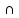 АВ1=В; АВ1=В;9. 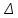 АВС-искомый. АВС-искомый.Какой следующий этап? (Доказательство) Ученик выходит к доске и записывает доказательство. Доказательство. АВС  АВ1С1(по углам) АВ1С1(по углам)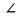 1-общий, 1-общий,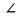 А-по построению А-по построению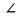 2= 2=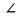 В1= В1=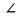 В (соответственные при ВС||В1С1 секущаяАВ1) В (соответственные при ВС||В1С1 секущаяАВ1)АК-биссектриса (по построению) 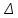 АВС –искомый. АВС –искомый.Остался последний этап. Какой же? (Исследование) Дети размышляют, обосновывают каждый этап построения. (Есть точки, принадлежащие прямой и ей не принадлежащие; На луче можно отложить только один угол, заданной градусной меры; Если 2 луча пересекаются, то они пересекаются только в одной точке;) Если, значит могут и не пересекаться. Какому условию должны удовлетворять градусные меры этих 2 углов? (Сумма внутренних углов треугольника равна 1800. Значит сумма 2 углов меньше 1800.) Единственность биссектрисы; Аксиома откладывания отрезка, Аксиома параллельности; Если прямая пересекает одну из параллельных прямых, то она пересекает и другую. |
