Физика пласта. Задача 6 Формула Дюпюи для безнапорных течений Выполнили Максимов С. и Гордиенко И. Проверил Игошин Д. Е. Тюмень 2021 г
 Скачать 92.47 Kb. Скачать 92.47 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего образования «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» ИНСТИТУТ МАТЕМАТИКИ И КОМПЬЮТЕРНЫХ НАУК Кафедра фундаментальной математики и механики Задача №6 «Формула Дюпюи для безнапорных течений» Выполнили: Максимов С. и Гордиенко И. Проверил: Игошин Д.Е. Тюмень 2021 г. Для приближенного описания течений со свободной границей были предложены Жюлем Дюпюи упрощающие предположения, которые выполняются для течений с пологой поверхностью депрессии. Движение жидкости описывается уравнением неразрывности и законом Дарси, которые имеют вид: 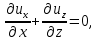 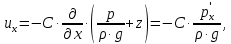 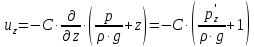 Основное предположение гидравлической теории заключается в том, что при малых углах наклона свободной поверхности к горизонту 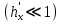 в любом вертикальном сечении пласта давление в фильтрующейся жидкости распределено по гидростатическому закону (что эквивалентно постоянству напора по сечению). Если эта гипотеза выполняется, то из закона Дарси имеет вид: в любом вертикальном сечении пласта давление в фильтрующейся жидкости распределено по гидростатическому закону (что эквивалентно постоянству напора по сечению). Если эта гипотеза выполняется, то из закона Дарси имеет вид: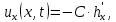 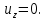 из чего следует, что скорость фильтрации в любой точке направлена горизонтально и не зависит от высоты: В частном случае стационарных течений форма поверхности депрессии находится из уравнения Лапласа: 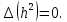 Уравнение Буссинеска 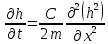 В случае стандартного плоскопараллельного течения уравнение Буссинеска дает формы свободной поверхности зависимость 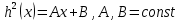 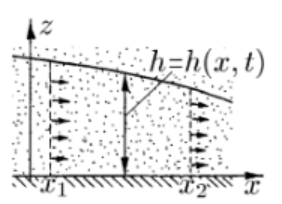 Постоянный объёмный расход жидкости выражается уравнением: 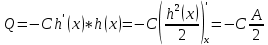 Выражение расхода через высоты свободной поверхности в точках 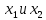 . .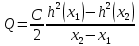 Так же получаем решение для стационарного безнапорного течения: 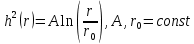 c расходом 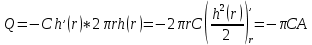 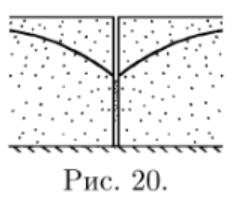 Для притока к скважине А>0 расход отрицательный. Расход можно задать следующим выражением: 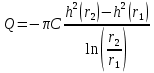 Эти соотношения называются формулами Дюпюи для пологой безнапорной фильтрации. A)Овраг Выберем следующие значения для задачи с оврагом:
Вычислим 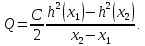 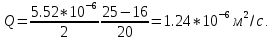 Выразим 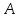 из уравнения из уравнения 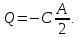 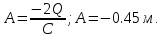 Рассчитаем 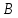 из уравнения из уравнения 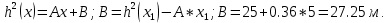 Собирая все полученные результаты: 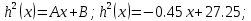 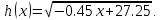 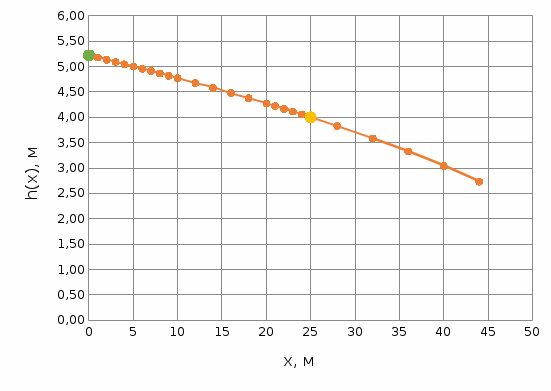 Рисунок 1. Формула свободной поверхности плоскопараллельного течения уравнения Буссинеска. Для проверки условия пологости возьмём 2 любые точки и рассчитаем отношение прироста 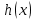 к приросту к приросту 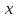 . .
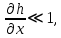 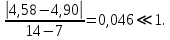 Б)Колодец
Вычислим: 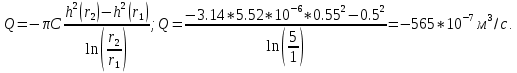 Выразим 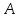 из уравнения из уравнения 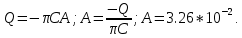 Выразим 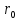 из уравнения из уравнения 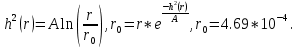 Получаем уравнения поверхности для осесимметричного безнапорного течения: 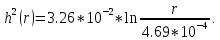 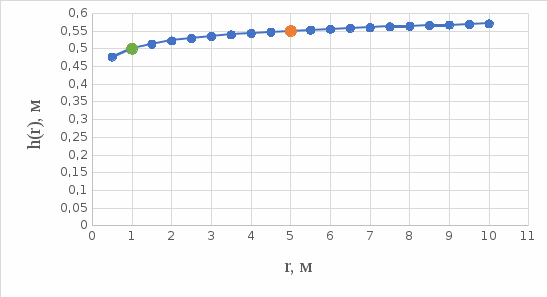 Рисунок 2. Форма свободной поверхности для осесимметричного безнапорного течения. Для проверки условия пологости возьмём 2 любые точки и рассчитаем отношение прироста 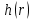 к приросту к приросту 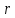 . .
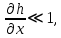 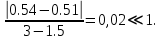 |
