решение в экономике. 3 Задачи решения. Задача 8 (10 баллов)
 Скачать 135.68 Kb. Скачать 135.68 Kb.
|
 Решения задач (вторая часть) Дата написания 15 апреля 2009 г. Количество задач 7 Сумма баллов 100 Время написания 180 минут Задача № 8 (10 баллов) — — Кривая предельной выручки фирмы-монополиста имеет вид MR(Q) = 400 4Q. Средние издержки постоянны. В точке оптимума эластичность спроса равна 3. Чемуравномаксимальноезначениеприбыли? Решение:− − — · − · − Линейный спрос вдвое более пологий, чем MR, значит, обратная функция спроса имеет вид: Pd= 400 2Q. Эластичность равна 3 в точке, где Q= 50, а P= 300. В этой (оптимальной) точке MR(50) = MC(50) = 200 = AC(50) (MC = AC, так как AC = const). Отсюда π= TR(50) TC(50) = 50 300 50 200 = 15 000 10 000 = 5 000. Ответ: 5 000. Задача № 9 (14 баллов) Робинзон собирает кокосы и ловит крокодилов и готовит из них особое блюдо — кро- кокосбургер. Для приготовления одного крококосбургера нужен один крокодил и три кокоса. Занимаясь только ловлей крокодилов, Робинзон может поймать 76 крокодилов в месяц; занимаясь только сбором кокосов, он может собрать 114 кокосов в месяц, а если бы кто-нибудь поставлял ему ингредиенты и он мог заниматься только готовкой, то приготовил бы за месяц 95 крококосбургеров. Альтернативные издержки занятия любым видом деятельности постоянны. Какоемаксимальноеколичествокрококосбургероввмесяцможетфактическипри- готовить и съесть Робинзон? Решение:Пусть X— количество часов в месяце, которым располагает Робинзон. Тогда 76Cr = 114Co = 95Bur = X, где Cr, Co и Bur — время, затраченное соответственно на ловлю одного крокодила, сбор одного кокоса и приготовление одного крококосбургера соот- ветственно. Ловя одного крокодила, Робинзон тратит X/76 часов; собирая кокос — X/114 ча- сов; занимаясь приготовлением крококосбургера — X/95 часов. Итого затраты времени на сбор ингредиентов и производство одного крококосбургера составят: X3XX + + 76 114 95 57XX = = 1140 20 часов. Следовательно, за Xчасов максимально возможно изготовить 20 крококосбургеров. Ответ: 20 крококосбургеров. Задача № 10 (12 баллов) Cпрос и предложение на совершенно конкурентных рынках подержанных автомо- билей в странах А и Б заданы следующими функциями:
Определите общий объем продаж подержанных автомобилей, направление и объ- ем экспорта, а также цены на подержанные автомобили в каждой из стран в усло- виях свободной торговли. Страна, импортирующая подержанные автомобили, с целью защиты своих произ- водителей ввела на каждую единицу импортируемого товара запретительнуюпошлину (в размере t руб. за единицу товара), которая делает торговлю между двумя странами невыгодной. Определите минимальное значение такой пошлины. Решение:Определим функции общего спроса и предложения, сложив горизонтально функ- ции в странах А и Б: Q d общ 90000 − 2P, если P≤ 40000, = 50000 − P, если 40000 ≤ P≤ 50000 Q s общ = 3P− 30000, если P≥ 10000 Найдем точку равновесия на пересечении функций суммарного спроса и предло- жения. Поскольку функция спроса задается по-разному на разных интервалах цен, необходимо выяснить, на каком интервале находится равновесие. Получаем решение: P∗ = 24000,Q∗ = 42000. В условиях свободной торговли цена в странах А и Б одинакова и равна 24000. Объем А внутреннего предложения в стране А: Qs= 2P− 20000 = 2 · 24000 − 20000 = 28000. А Объем внутреннего спроса в стране А: Qd= 40000 − P= 40000 − 24000 = 16000. — Следовательно, страна А экспортирует машины в количестве Ex = 28000 16000 = 12000, а импортирует страна Б в том же количестве 12000. Обозначим минимальную запретительную пошлину через t, тогда в стране Б цены будут на t выше, чем в стране А: PБ = PА + t. При такой пошлине избыточный спрос в стране Б будет равен нулю: 50000 − PБ − (PБ − 10000) = 0. Поэтому PБ = 30000 = PА + t. При этом PА не зависит от избыточного спроса в стране Б (он равен нулю) и определяется спросом и предложением внутреннего рынка в стране А: Qd= 40000 − P= Qs= 2P− 20000 ⇒ 3PА = 60000 ⇒ PА = 20000. Следовательно, t= 30000 − 20000 = 10000. Задача № 11 (20 баллов) Фирма «В два касанияк является монополистическим конкурентом на рынке во- лейбольных мячей. В последнее время владельцу фирмы Н. Е. Удачнику можно только посочувствовать: его бизнес переживает не лучшие времена1. Спрос на продукцию фир- мы линеен, однако в последнее время он стал настолько низким, что фирме неважно, уходить с рынка или производить 40 единиц продукции, — и это при наиболее проду- манном, рациональном поведении! Средние переменные издержки при данном объеме выпуска аж втрое больше предельных, а единственным для фирмы шансом покрыть выручкой постоянные издержки было бы установление цены, равной 20. Представьте, что вы являетесь сотрудником государственной службы, оказывающей поддержку малому бизнесу. Проанализируйте ситуацию, в которой оказалась фирма «В два касания», гра- фически, изобразив на одном рисунке примерные графики спроса, MR, MC, AVC, AFC. Определитеуравнениекривойспросанапродукциюфирмы. Определитевеличинуаккорднойсубсидии,необходимойдлявыведенияфирмы Н. Е. Удачника на уровень безубыточности. Решение:В оптимуме фирме неважно, производить 40 единиц продукции или уходить с рынка, значит, MR(40) = MC(40), π(40) = π(0) = − FC ⇓ P(40) = AVC(40)— Более того, раз фирма не может получить прибыль большую, чем ( FC), то в дру- гих точках P <AVC, и значит, график AVC должен касаться графика спроса в точке, где Q = 40. Если существует лишь единственная цена (P= 20), при которой выручка равна постоянным издержкам, то это цена, при которой выручка максимальна. Это также и единственная цена, при которой средняя выручка (цена) равна средним постоянным издержкам. Отсюда следует, что график спроса должен касатьсяграфика AFC в точке P= 20 и при таком объеме выпуска, где функция MR пересекает ось Q. Пусть обратная функция спроса задается уравнением P= a− bQ. Тогда 3 = AVC(40) = P(40) = a−b·40 ⇒ a= 100b. MC(40) MR(40) a− 2b· 40 — Как мы выяснили, максимальную выручку фирма может получить при P= 20. Для линейной функции спроса цена, максимизирующая выручку, равна a/2, значит, a = 40. Функция спроса, таким образом, имеет вид P= 40 0,4Q. Понятно, что величина аккордной субсидии, выводящей фирму на уровень безубы- точности, должна быть в точности равна текущим убыткам фирмы (ведь после полу- чения аккордной субсидии фирма не изменит выпуск). Значит, S = −π(40) = FC = TRmax = 20 · 100/2 = 1 000. 1Кризис! Графически ситуация сводится к следующему: P 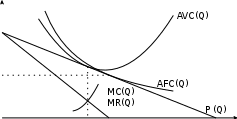 20 20Q 40 Вот такие «Два касанияк! Задача № 12 (12 баллов) Фирма «Акерлоф Ltd.к является монополистом на рынке лимонов. В краткосрочном периоде данная фирма использует единственный переменный фактор производства — труд, и закупает его на совершенно конкурентном рынке. Известно, что в точке опти- мума коэффициент эластичности выручки данной фирмы по выпуску составил 0,37, а средняя производительность труда достигла максимального значения и составила 500. Скольколимоновможеткупитьрабочийэтойфирмынаоднузарплату? Решение:Запишем условие оптимума фирмы-монополиста: MRPL= w, или, что то же самое, MR · MPL= w. Разделим обе части уравнения на рыночную цену лимона (p): MR w p· MPL= p. Но эластичность выручки по выпуску как раз равна: · TR' Q= MR . TR p Кроме того, в точке оптимума APL= MPL, так как APL= max APL. Значит, TR Q E· AP ww p p L = ⇒ = 500 · 0,37 = 185. Это и есть ответ на вопрос задачи: величина w/pкак раз показывает реальную зарплату рабочего, выраженную в лимонах. Ответ: 185. Задача № 13 (14 баллов) Заботясь о сохранении редких видов рыб, государство собирается ввести на рынке черной икры потоварный налог. С помощью этой меры оно надеется не только ограни- чить потребление икры, но и получить средства для финансирования дорогостоящей экологической программы. Таким образом, убивая двух зайцев, можно будет спасти тысячи рыб! C помощью налога нужно собрать не менее 48 216 тыс. руб. — именно столько стоит программа. Экономисты правительства оценили для данного рынка кривую Лаффера при введении потоварного налога: 200900t T= (1 + t)2 , где t— ставка налога (в тыс. руб.), а T— общая сумма налоговых поступлений (также в тыс. руб.). На сколько процентов государству удастся максимально сократить объем потреб-ления икры? Решение:Найдем, какие ставки налога обеспечат как минимум нужную сумму: 200900t2 3 T= (1 + t)2 ≥ 48216 ⇒ 3 ≤ t≤ 2 . Государство стремится минимизировать объем продаж черной икры, значит, оно установит максимальную налоговую ставку из всех подходящих: t = 3/2. · Для того чтобы найти изменение рыночного объема, вспомним, что сумма налоговых поступлений при введении потоварного налога равна tQ(t), где Q(t) — равновесный объем, который установится на рынке при введении налога по ставке t. 200900t 200900 T= (1 + t)2 = t· Q(t) ⇒ Q(t) = (1 + t)2 . До налогообложения рыночный объем равнялся Q(0), то есть 200 900. После введе- ния налога рыночный объем составит: 2 25 Q 3 = 200900 · 4 . Объем продаж изменится в 4/25 раза, то есть сократится на 84 %. Ответ: на 84 %. Задача № 14 (18 баллов) В программном документе правящей партии страны Тугриндии (национальная ва- люта — тугр) должно было быть написано: «поддерживать ежегодный темп прироста реальногоВВПстранынауровне10%иза20летобеспечитьутроениеегоотношения к размеру государственного долга . Однако по невнимательности секретарши напе- чатано оказалось иное: «обеспечиватьежегодныйприростреальногоВВПстранына 10 млн тугров и за 20 лет обеспечить его утроение. Как ни странно, задание, записанное секретаршей, удалось реализовать. РассчитайтетемпприростареальногоВВПстраныза13-йгод. РассчитайтесреднегодовойтемпростареальногоВВПстраныза20лет. НарисуйтеграфикизмененияреальногоВВПстранывовремени. Нарисуйте график изменения реального ВВП страны во времени для первона- чально предполагавшейся программы. ВосколькоразизменилосьотношениеВВПкразмеругосударственногодолга в ходе реализации «ошибочной» программы? Предполагаем, что долг при «ошибочной» программеизменялсятакже,какдолженбылбыизменятьсяприправильной. Удалосьлиправительствуобеспечитьустойчивыедолгосрочныетемпыприро- ста реального ВВП? Решение:Поскольку ошибочный план удалось реализовать, то Y0 + 20 · 10 = 3Y0,Y0 = 100,Y20 = 3Y0 = 300. Темп прироста реального ВВП страны за 13-й год. g13 = Y13−Y12 100 % ≈ 4,545 %. · Y 12 Среднегодовой темп роста реального ВВП страны за 20 лет: (1 + g) = 2√0 3 ≈ 1,056. Изменение реального ВВП страны во времени представляет собой линейную воз- растающую функцию. График изменения реального ВВП страны во времени:  Y(t) Y(t)t Изменение реального ВВП страны во времени для предполагавшейся программы представляет собой показательную выпуклую вниз функцию:  Y(t) Y(t)t Планировалось: |
