Оформление задач по геометрии. Решение задач и оформл. 7класс. Задача Дано авс равнобедренный, ао со. Доказать аво сво. Доказательство
 Скачать 44.38 Kb.
|
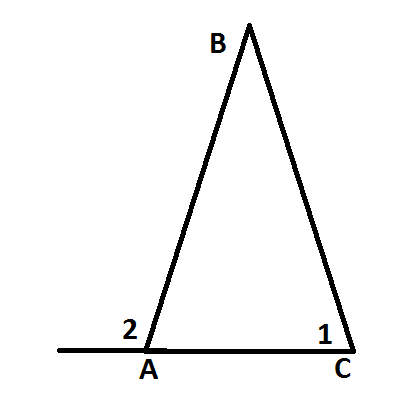 Задача 1.Дано: ∠ 1 = 75°, ∠ 2 = 105° Доказать : ∆АВС – равнобедренный. Доказательство : ∠ВАС = 180° – ∠ 2 = 180° – 105° = 75° ( по свойству смежных углов.) В 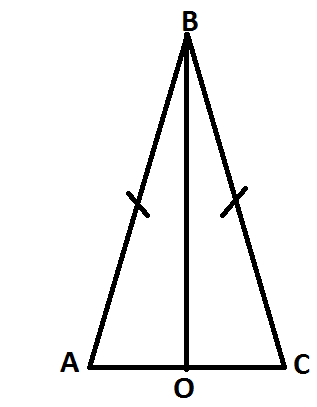 ∆АВС ∠ ВАС = ∠ ВСА = 75°. А так как это углы при основании АС треугольника ∆АВС и они равны, следовательно , ∆АВС - равнобедренный.Задача 2. Дано: ∆АВС – равнобедренный, АО = СО. Доказать : ∆АВО = ∆СВО. 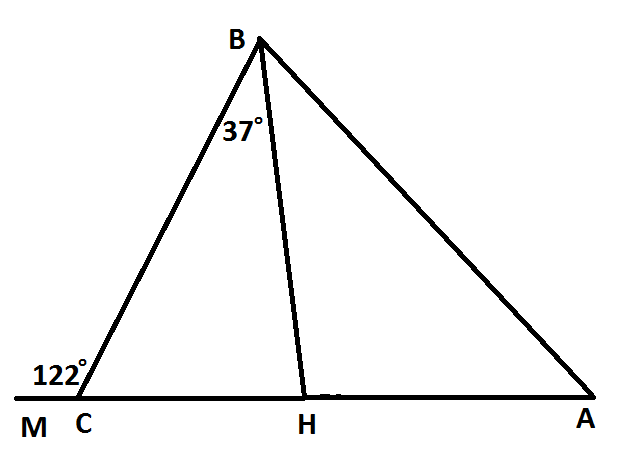 Доказательство : По условию АО = СО, значит, ВО является медианой в ∆АВС. Учитывая, что ∆АВС – равнобедренный ( по условию), то медиана, проведённая к основанию является биссектрисой, значит ∠ АВО = ∠ СВО по определению биссектрисы угла. Рассмотрим ∆АВО и ∆СВО . АВ = ВС т.к. ∆АВС – равнобедренный. ∠ АВО = ∠ СВО доказано в п.1 ВО - общая сторона. Значит, ∆АВО = ∆СВО по первому признаку равенства треугольников. Задача 3 . П 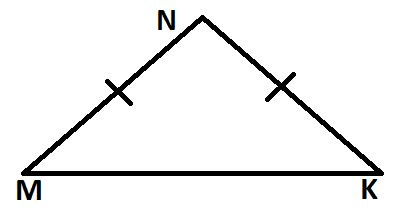 ериметр равнобедренного треугольника равен 48 см, а боковая сторона – 15 см. Найдите основание этого треугольника.Дано: ∆ MNK – равнобедренный. 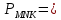 48 см, MN = 15 см.Найти : MК. Решение. По условию ∆ MNK – равнобедренный, значит, NK = MN. MK = 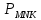 – 2MN = 48 – 2 · 15 = 48 – 30 = 18 (см).Ответ : МК = 18 см. Задача 4. ВН – биссектриса ∆АВС. Найдите угол ВАС, если ∠ВСМ = 122°, ∠СВН = 37°. Решение. 1. По свойству смежных углов ∠ВСА = 180° – ∠ВСМ = 180° – 122° = 58°. 2. По условию ВН – биссектриса ∆АВС, значит, ∠АВС = 2 ∠СВН = 37° · 2 = 74°. 3. Зная, что сумма углов в треугольнике равна 180°, получим: ∠ВАС = 180° - (∠ВСА + ∠АВС) = 180° - (58° + 74°) = 180° - 132° = 48°. Ответ: ∠ВАС = 48°. |