физика ргр. 2вар 3 сем. Задача Интерференция света от двух когерентных источников 7

Название	Задача Интерференция света от двух когерентных источников 7
Анкор	физика ргр
Дата	08.12.2022
Размер	0.54 Mb.
Формат файла
Имя файла	2вар 3 сем.doc
Тип	Задача #835050

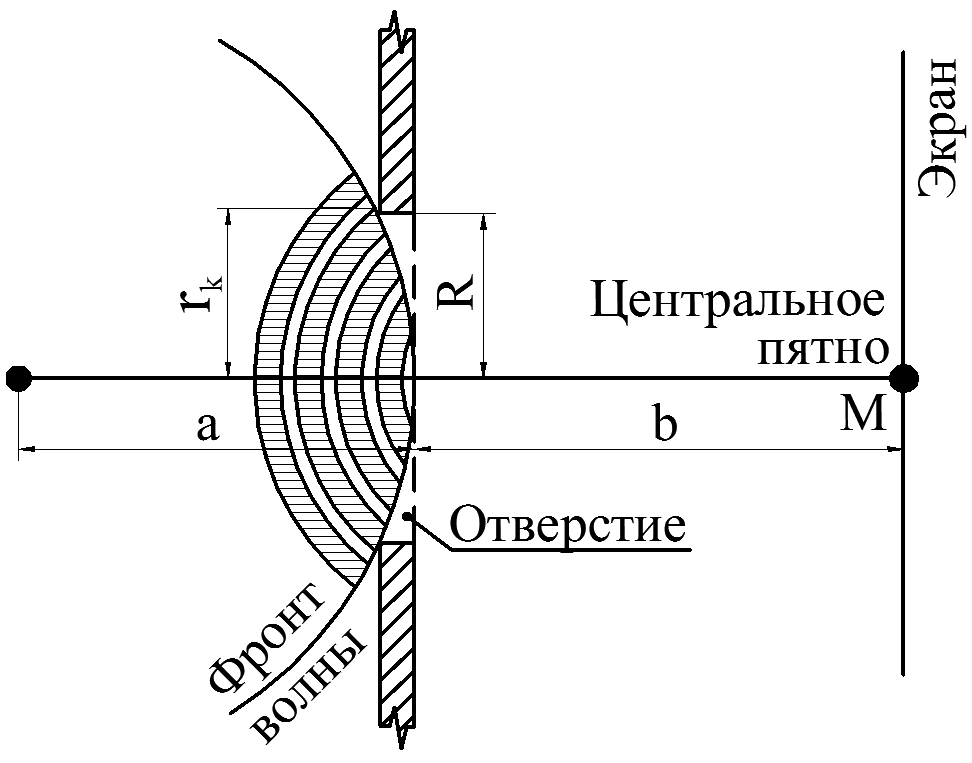
Содержание

Задача 1. Интерференция при отражении света от тонких пластинок либо при прохождении света сквозь эти пластинки 3

Задача 2. Интерференция света от двух когерентных источников 7

Задача 3. Дифракция света на круглом отверстии или на диске (метод зон Френеля) 9

Задача 4. Дифракция света на дифракционной решетке (дифракция Фраунгофера) 11

Задача 5. Поляризованный свет. Вращение плоскости поляризации света 14

Задача 1. Интерференция при отражении света от тонких пластинок либо при прохождении света сквозь эти пластинки

Световая волна с плоским фронтом (параллельный пучок лучей) с длиной волны λ₀ = 0,5 мкм падает в вакууме под углом α на стопу из 3 плоскопараллельных прозрачных пластинок (пленок) (рис. 1а) с абсолютными показателями преломления n₁, n₂, n₃ и соответствующими толщинами h₁, h₂, h₃.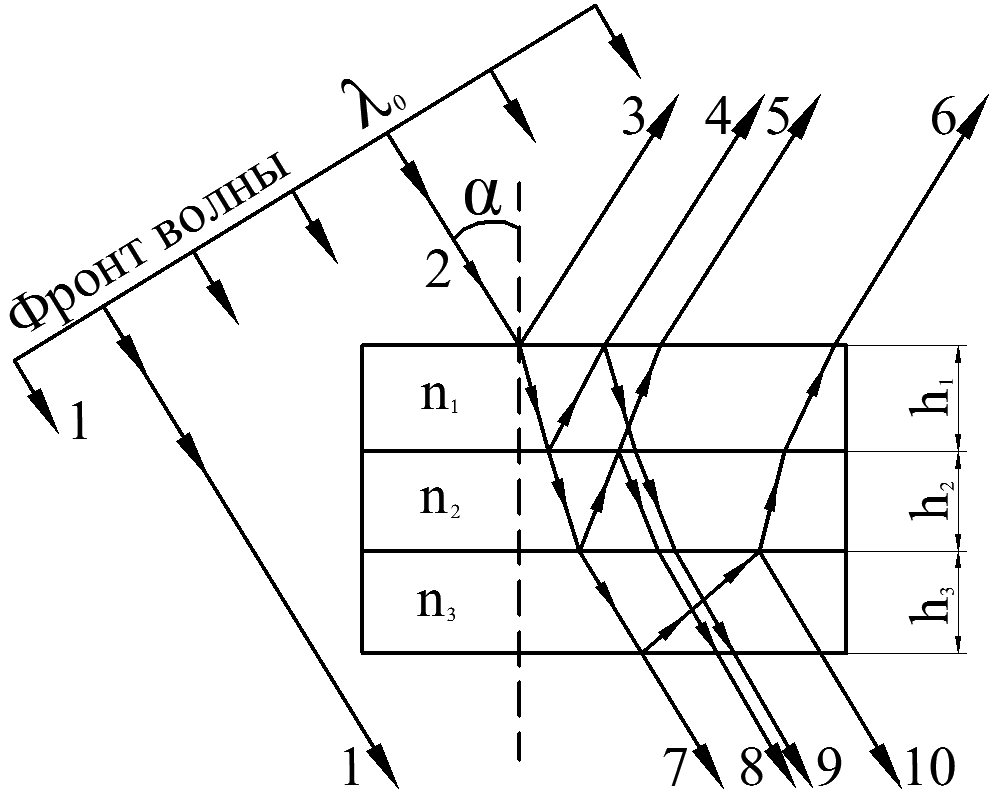

Рис. 1а – Интерференция света в параллельных прозрачных пластинках

Определить оптическую разность хода δ проходящих лучей 3 и 4.

Максимум или минимум освещенности на экране дадут эти волны (лучи) при наложении?

Нарисуйте конкретный чертеж, показывающий ход двух лучей.

Дано:

λ₀ = 0.5 мкм = 0,5∙10^-6 м

α = 45º

h3=3

n3=1.5

n₂ = 1,8

Найти: δ = ?

Решение:

В общем виде оптическая разность хода δ лучей (волн) 3 и 4 будет равна

где L₃, L₄ – оптические длины путей каждого из лучей 3 и 4 соответственно.

В соответствии с условием построим чертеж, показывающий ход двух означенных выше лучей.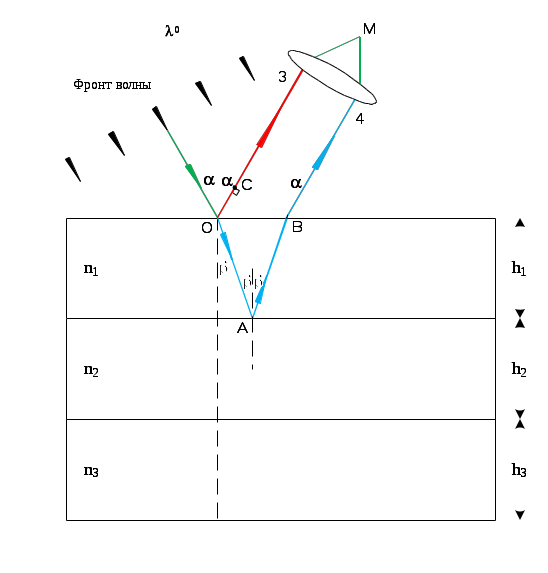

Рис. 1б – Ход лучей 3 и 4

Луч 3, согласно условию, отражаясь от первой пластинки в точке А, проходит по геометрической траектории ОCМ (рис. 1б), следовательно, оптическая длина пути данного луча будет определяться как

при этом, поскольку n₁ > n₀ (луч падает из воздушной среды на стекло), то в оптический путь луча 3 включена дополнительная разность хода λ₀/2, возникающая при отражении волны в точке О.
Луч 4, согласно условию, проходит стопу пластинок по геометрической траектории ОАВM (рис. 1б), следовательно, оптическая длина пути данного луча будет определяться как

при этом, поскольку n₁ > n₂, дополнительной разности хода, возникающей при отражении волны в точке A, в оптический путь луча 4 не добавляется.

Для удобства вычислений обозначим равные отрезки путей каждого луча как

a = ОА = АB = СD, b = ОC, с = CM = BM.

Тогда оптическая разность хода δ лучей 3 и 4 будет равна

Из геометрического построения и закона Снеллиуса (закона преломления лучей) имеем, что, поскольку

,

то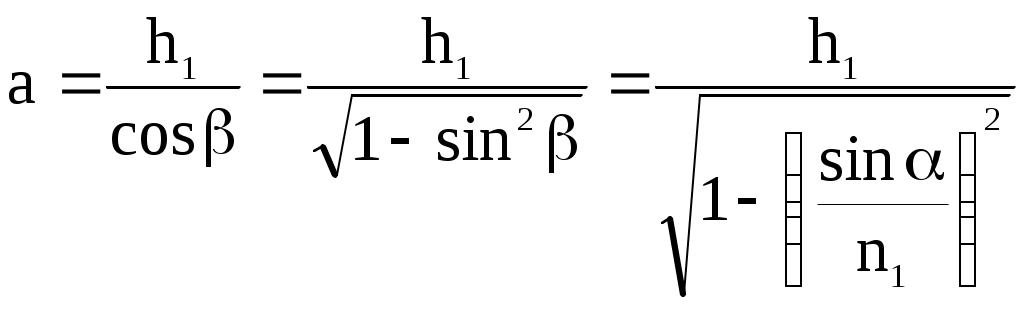

.

Упрощая и подставляя исходные данные, получаем, что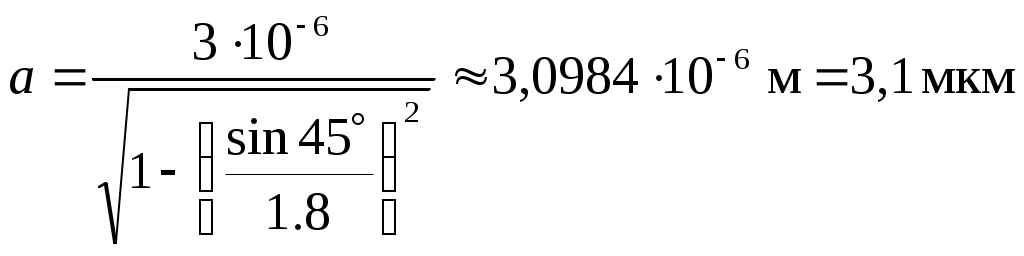

.

Отрезок пути b = OC вычисляется как

поскольку ОВ есть основание равнобедренного треугольника ОАВ, как явствует из геометрического построения, то

отсюда

Тогда оптическая разность хода δ лучей 3 и 4 будет равна

Поставляя числовые данные, производим расчет

Интерференционный максимум или минимум будет наблюдаться на экране, зависит от четного или нечетного числа длин полуволн

, которое укладывается в δ:

Как нетрудно видеть, оптическая разность хода δ составляет четное число длин полуволн, следовательно, волны 3 и 4 будут усиливать друг друга – дадут интерференционный максимум на экране в точке М.

Задача 2. Интерференция света от двух когерентных источников

Расстояние между двумя когерентными источниками света S₁ и S₂ равно d. Источники, испускающие монохроматический свет с длиной волны в вакууме λ₀ = 0,5 мкм, расположены на расстоянии L от экрана. Рассмотреть два случая: 1) волны распространяются в однородной среде с абсолютным показателем преломления n_ср; 2) на пути первой волны помещена в ту же среду прозрачная пластинка (пленка) толщиной h с абсолютным показателем преломления n_пл (рис. 2).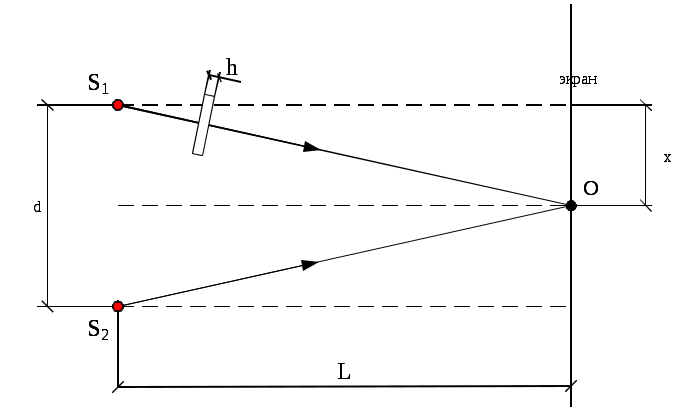

Рис. 2 – Интерференция света от двух когерентных источников (x << L, d << L)

Определить для обоих случаев оптическую разность хода δ двух волн в точке O, расположенной на одинаковом расстоянии от источников. Определить разность фаз Δφ двух интерферирующих волн в той же точке. Какая освещенность будет в этой точке – минимальная или максимальная? Нарисуйте конкретный чертеж, соответствующий варианту 2.

Дано:

λ₀ = 0,5 мкм = 0,5∙10^-6 м

Рассматриваемая точка на экране – точка О

L = 2 м

h = 6,5 мкм = 6,5∙10^-6 м

n_cp = 1,5

n_пл = 2,0

Найти: 1) δ = ?; 2) Δφ = ?

Решение:

Чертеж, соответствующий варианту 2, указан на рис. 2. Из рис. 2 видно, что для точки О

δ = L₁ – L₂,

где L₁ и L₂ – оптические пути соответствующих лучей.

1) С учетом геометрии следует для случая 1 (без пластинки):

L₁ = L₂ = n_cp

;

,

т.е. интерференционной картины наблюдаться не будет, в точке А – максимум освещенности, т.к.

.

2) Для случая 2 (с пластинкой):

δ = L₁ – L₂ =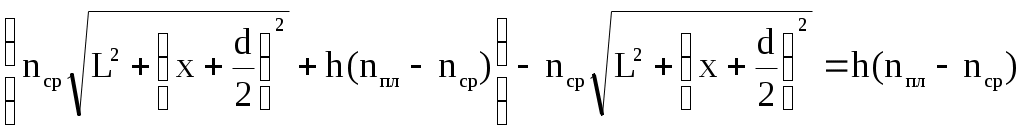

;

подставляя исходные данные, получаем

В точке А будет наблюдаться минимум освещенности, так как

– нечетное число длин полуволн;

– нечетное число π.

Задача 3. Дифракция света на круглом отверстии или на диске
(метод зон Френеля)

На круглое отверстие радиусом R от точечного источника S падает свет с длиной волны λ. На пути лучей, прошедших через отверстие, помещают экран (рис. 3). Расстояние от точечного источника до отверстия равно а; расстояние от отверстия до экрана, на котором ведется наблюдение дифракционной картины, равно b. В отверстии укладывается k зон Френеля. Каков размер радиуса отверстия? Темное или светлое пятно получится в центре дифракционной картины?

Рис. 3 – Дифракция света на отверстии радиуса R

Дано:

Дифракция на отверстии

λ = 0,5 мкм = 0,5∙10^-6 м

а = м

b = м

k = 4

Найти:

пятно – темное или светлое?

Решение:

Радиус k-й зоны Френеля определяется по формуле

,

при этом радиус последней k-й зоны, укладывающейся в отверстие, равен радиусу отверстия

r_k = R,

следовательно,

Центральное пятно будет тёмным, так как в отверстии укладывается чётное число (k = 4) зон Френеля.

Ответ: 1) R = 2 мм; 2) центральное пятно – тёмное.

Задача 4. Дифракция света на дифракционной решетке
(дифракция Фраунгофера)

На дифракционную решетку Д нормально падает монохроматический свет с длиной волны λ (фронт волны – плоский). На экране Э, расположенном за собирающей линзой параллельно решетке и отстоящем от нее на расстоянии L, наблюдается дифракционная картина (рис. 4). Расстояние между двумя дифракционными максимумами k-го и i-го порядков равно ℓ. Общее число главных максимумов, получаемых с помощью этой решетки, равно N.

Определить расстояние от решетки до экрана L, постоянную дифракционной решетки d и число n штрихов решетки на 1 мм ее длины.

Нарисуйте конкретный чертеж, соответствующий варианту 2.

Рис. 4 – Дифракция при прохождении света через дифракционную решетку
Дано:

λ =

ℓ = 10 см = 0,10 м

k = -1

i = -3

N =

Найти: 1) L = 1.5 2) d = ? 3) n = ?

Р
Рис. 4б.
ешение:

Общее число N главных максимумов

N = 2k_max + 1,

где k_max получаем при φ = 90⁰:

.

Следовательно,

Отсюда постоянная дифракционной решетки

Подставляя исходные данные, имеем

Число штрихов на 1 мм решетки

,

то есть 40 штрихов на 1 мм.

Условие для максимума i-го порядка:

dsinφ_k = iλ,

а для k-го

dsinφ_i = kλ.

Будем считать углы дифракции φ отрицательными слева от центрального максимума и положительными справа. Обычно углы дифракции φ малы, поэтому

.

Получаем

dtgφ_i = 0, dtgφ_k = λ,

или

.

Отсюда

.

Так как ℓ = l₁ + l₂, то получаем

ℓ

Отсюда искомое расстояние от решетки до экрана

L = ℓd/λ.

Подставляя исходные данные, имеем

Задача 5. Поляризованный свет. Вращение плоскости поляризации света

Кристаллическая пластинка, обладающая оптической активностью с постоянной вращения α, помещена между двумя николями – поляризатором и анализатором (рис. 1а и 1б). На поляризатор падает линейно поляризованный свет, интенсивность которого I₀. После прохождения через поляризатор интенсивность света равна I₁, а после прохождения через анализатор – I₂. Угол между направлением колебаний светового вектора волны линейно поляризованного света, падающей на поляризатор, и главной плоскостью поляризатора равен φ₁, а угол между главными плоскостями анализатора и поляризатора равен φ₂ (углы отсчитываются по часовой стрелке). Кристаллическая пластинка свет не поглощает, и толщина ее равна d. В николях теряется по 10% проходящего через них света (неидеальные поляризатор и анализатор). Найти неизвестную величину, используя данные табл. 1. На рисунке показать углы φ₂, φ₃ и Δφ, где φ₃ – угол поворота плоскости поляризации света в пластинке, Δφ – угол между

волны, падающей на анализатор, и главной плоскостью анализатора (см. рис. 5б).

Рис. 5а – Прохождение света через систему поляризатор – вещество – анализатор
(I

- интенсивность света на выходе из кристаллической пластинки)

Рис. 5б – Направление колебаний

(состояние поляризации) световой волны при прохождении ее через систему поляризатор – вещество – анализатор

Дано:

На систему падает линейно поляризованный свет

φ₁ = 45º

I₂/I₀ = ?

 = +30 град/мм

d = 2 мм = 2∙10^-3 м

k = 10%

Найти: 1) I₁/I₀ = ? 2) φ₂ = ?

Решение:

1. В случае, когда на поляризатор падает волна линейно поляризованного света для идеального поляризатора справедливо соотношение