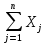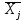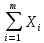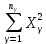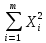Норма права. Задача Исчисление показателей вариации в дискретном ряду Распределения
 Скачать 81.73 Kb. Скачать 81.73 Kb.
|
|
Примеры расчета показателей вариации Задача 1. Исчисление показателей вариации в дискретном ряду Распределения Условие: имеются данные дискретного ряда распределения по числу поливов сахарной свеклы (таб. 1.8) Определить показатели вариации: размах вариации, среднее линейное отклонение, дисперсию (по основной формуле), среднеквадратическое отклонение, коэффициент осцилляции, линейный и квадратический коэффициент вариации. Решение. Составим макет таблицы 1.8. и запишем исходные данные в графы 1 и 2. Таблица -1.8. Исходные и расчетные данные для определения показателей вариации в дискретном ряду распределения
1.Определим размах вариации. R=Xmax - Xmin = 7 -1= 6 (поливов) Вывод: По хозяйствам максимальные различия составляют 6 поливов . 2.Вычислим среднее линейное отклонение по формуле L= 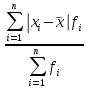 где xi - значение признака, 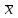 - средняя арифметическая, - средняя арифметическая, fi- частота встречаемости признака в совокупности. а) определим абсолютное отклонение каждой варианты от средней 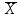 =4 (гр. 3); =4 (гр. 3);б) определим абсолютные отклонения, взвешенное соответствующими частотами, и их сумму ( графа 4); в) рассчитаем среднее линейное отклонение L = 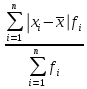 = = 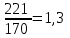 Вывод : среднее отклонение индивидуальных значений признака от средней величины составляет 1,3 полива. 3.Исчислим дисперсию по основной формуле 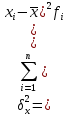 а) вычислим квадраты отклонений от средней ( графа 5); б) определим взвешенные частотами квадраты отклонений и их сумму (гр. 6) в) вычислим дисперсию 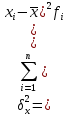 = =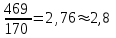 Вывод: средний квадрат отклонений вариант от средней составил 2,8 полива2. 4. Рассчитаем среднее квадратическое отклонение как корень квадратный из дисперсии 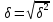 = =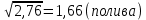 Вывод: среднее квадратическое отклонение показывает, что все варианты отклоняются от средней величины в среднем на 1,7 полива. Примечание: Если распределение близко к нормальному, или симметричному, то между среднеквадратичным и среднелинейным отклонением существует взаимосвязь 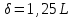 или L=0,8 δ. или L=0,8 δ.Определим относительные показатели вариации. 5. Коэффициент осцилляции 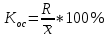 = = 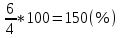 Вывод: относительная максимальная колеблемость поливов по хозяйствам высокая. 6.Относительное линейное отклонение ( линейный коэффициент вариации) 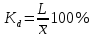 = =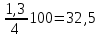 Вывод: средняя колеблемость поливов по хозяйствам сравнительно высокая и составляет 32,5 %, что свидетельствует об умеренной неоднородности совокупности. 7. Определим коэффициент вариации (квадратический коэффициент вариации): 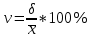 = =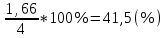 Вывод: коэффициент вариации указывает на то, что мера колеблемости в данном ряду распределения высокая (более 33 %) , и совокупность является неоднородной по изучаемому признаку. Задача 2. Исчисление показателей вариации в интервальном ряду распределения Условие: имеются данные интервального ряда распределения по урожайности сахарной свеклы (таб. 1.9.) Определить показатели вариации. Дисперсию вычислить по основной и рабочей формулам. Решение. 1.Определим размах вариации. R=Xmax - Xmin = 58,0 - 22,0 = 36,0 (т/га) Вывод: В изучаемой совокупности хозяйств максимальные различия в урожайности составляют 36 т/га. 2.Вычислим среднее линейное отклонение по формуле L= 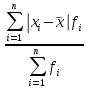 где xi - значение признака, 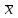 - средняя арифметическая, , fi- частота встречаемости признака в совокупности. - средняя арифметическая, , fi- частота встречаемости признака в совокупности.а) определим абсолютное отклонение каждой варианты от средней 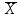 =39,5т/га (графа 3); =39,5т/га (графа 3);б) определим абсолютное отклонение, взвешенное соответствующими частотами, и их сумму ( графа 4); в) рассчитаем среднее линейное отклонение L = 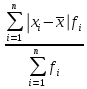 = = 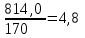 Вывод : среднее отклонение признака от средней величины составляет 4,8, т.е. в среднем по хозяйствам урожайность сахарной свеклы отклоняется от средней урожайности на 4,8 т/га. 3.Исчислим дисперсию по основной формуле 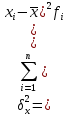
а) вычислим квадраты отклонений от средней (графа 5); б) определим взвешенные частотами квадраты отклонений и их сумму (гр. 6). Примечание: квадраты отклонений следует считать при достаточно большой степени точности, (до 0,0000). в) вычислим дисперсию 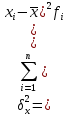 = =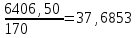 4. Определим дисперсию по рабочей формуле: 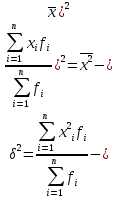 а) найдем квадраты значений признака (графа 7); б) рассчитаем взвешенные частотами квадраты значений признака и их сумму (графа 9); в) вычислим дисперсию 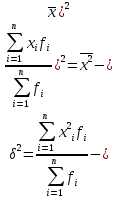 = =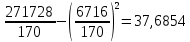 5. Рассчитаем среднее квадратическое отклонение как корень квадратный из дисперсии 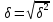 = =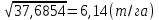 Вывод: среднее квадратическое отклонение показывает, что все варианты отклоняются от средней величины в среднем на 6, 14 т/га. Определим относительные характеристики вариации. 6. Коэффициент осцилляции 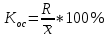 = = 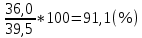 Вывод: относительная колеблемость крайних значений урожайности по хозяйствам высокая. 7.Относительное линейное отклонение 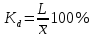 = =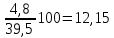 Вывод: средняя колеблемость урожайности по хозяйствам низкая и составляет 12,15 %, что свидетельствует об однородности совокупности. 8. Определим коэффициент вариации: 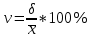 = =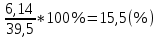 Вывод: Средняя мера колеблемости в данном ряду распределения невысокая (менее 33 %) , и совокупность является однородной по изучаемому признаку. Задача 3. Правило сложения дисперсий (разложения объемов вариаций) (основа дисперсионного анализа) Условие: имеются данные по урожайности 14 кустов винограда разных сортов. (таб.1.10) Рассчитать: общую, межгрупповую и внутригрупповую дисперсии и объемы вариации, применив основные и рабочие формулы. По расчетным данным доказать справедливость теоремы. Определить эмпирический коэффициент детерминации и корреляционное отношение. Сделать выводы о связи сортов и урожайности винограда. Таблица -1.10. Урожайность кустов винограда разных сортов, кг
Решение. Правило сложения дисперсий : При сгруппированных единицах совокупности дисперсия общая ( 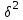 общ) равна сумме межгрупповой ( общ) равна сумме межгрупповой (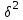 мгр) и внутригрупповой дисперсий ( мгр) и внутригрупповой дисперсий (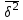 внтр). внтр).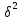 общ = общ =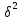 мгр + мгр +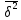 внтр внтр При этом общая дисперсия представляет собой средний квадрат отклонений значений признака от средней по всей совокупности. Межгрупповая дисперсия –это средний квадрат отклонений групповых средних от общей средней величины по всей совокупности. Внутригрупповая дисперсия представляет собой среднюю арифметическую взвешенную из внутригрупповых дисперсий. Взвешивание проводится по числу единиц совокупности в каждой группе. Каждая из внутригрупповых дисперсий представляет средний квадрат отклонений индивидуальных значений признака в пределах каждой группы от своей групповой средней величины. Каждая из дисперсий рассчитывается как отношение объемов вариации к численности единиц совокупности 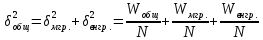 Поскольку знаменатели дробей равны между собой, равенство справедливо также для числителей, т.е. общий объем вариации равен сумме межгруппового и внутригруппового объемов вариации. Таким образом, на первом этапе расчетов докажем равенство объемов вариаций, на втором – равенство дисперсий. Вычисление объемов вариаций проведем двумя способами: по основным и рабочим формула. Для расчета объемов вариаций необходимо определить общую среднюю по совокупности и групповые средние по каждой группе. Общая средняя величина по совокупности равна: 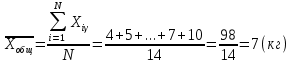 . .Групповые средние равны: 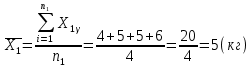 . . 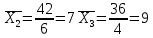 Полученные значения запишем в последнюю графу таблицы 1.10. 1. По основным формулам объемы вариации составят: Общий объем вариации 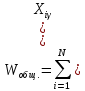 = (4-7)2+(5-7)2+(5-7)2+…(10-7)2=50 = (4-7)2+(5-7)2+(5-7)2+…(10-7)2=50Межгрупповой объем вариации 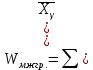 =(5-7)2 * 4 + (7-7)2 * 6 +(9-7)2* 4 =32 =(5-7)2 * 4 + (7-7)2 * 6 +(9-7)2* 4 =32Для расчета внутригруппового объема вариации по совокупности в целом предварительно определим внутригрупповой объем вариации в каждой группе. Объем вариации для первой группы равен 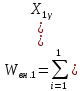 =(4-5)2+(5-5)2+(5-5)2+(6-5)2= 2 =(4-5)2+(5-5)2+(5-5)2+(6-5)2= 2Объем вариации во второй группе составляет 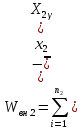 = (7-7)2+(6-7)2+(8-7)2+(9-7)2+(5-7)2+(7-7)2=10 = (7-7)2+(6-7)2+(8-7)2+(9-7)2+(5-7)2+(7-7)2=10Объем вариации в третьей группе равен 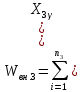 =(9-9)2+(10-9)2+(7-9)2+(10-9)2=6 =(9-9)2+(10-9)2+(7-9)2+(10-9)2=6Складывая Wвн.1 , Wвн.2 и Wвн.3 , получаем внутригрупповой объем вариации по совокупности Wвн.= Wвн.1 + Wвн.2 + Wвн.3 =2+10+6=18 Рассчитанные показатели доказывают справедливость равенства объемов вариации Wобщ.= Wмежгр.+ Wвнутр 50 = 32 + 18 2.Рассчитаем объемы вариации признака по рабочим формулам. Для этих расчетов необходимы дополнительные характеристики, которые получим в таблице 1.11 Таблица -1.11. Таблица квадратов
Общий объем вариации равен: 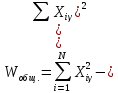 736 - 736 - 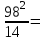 736 - 686 = 50. 736 - 686 = 50.Межгрупповой объем вариации определим по формуле: 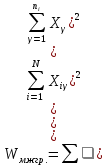 = = 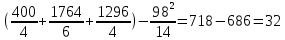 . .Внутригрупповой объем вариации по рабочей формуле равен: 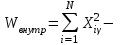 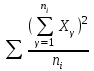 = 736-718=18 = 736-718=18Таким образом, по рабочим формулам доказали справедливость равенства Wобщ.= Wмжгр.+ Wвнгр. 50 = 32 + 18 3.Для расчета дисперсий необходимо разделить объемы вариаций на численность совокупности 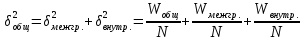 = = 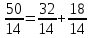 ; 3,5714=2,2857+1,2857 ; 3,5714=2,2857+1,28574. Для оценки связи вариации урожайности с группировочным признаком (сортами) рассчитаем удельный вес межгрупповой дисперсии в общей дисперсии, называемый коэффициентом детерминации. 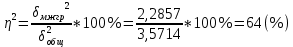 Коэффициент детерминации 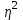 показывает, что 64% вариации урожайности кустов винограда в совокупности обусловлено сортовыми различиями, остальные 36% - другими факторами. показывает, что 64% вариации урожайности кустов винограда в совокупности обусловлено сортовыми различиями, остальные 36% - другими факторами.Корреляционное отношение равно η = 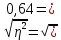 0,8. 0,8.По предложенной Чэддоком шкале значение 0,8 в задаче свидетельствует о сильном влиянии сортов на урожайность винограда. Шкала Чеддока
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

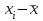 при
при 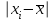
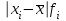
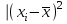
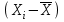
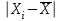 f
f