практическая 4. Задача Монету подбрасывают три раза. Составить закон распределения случайной величины X числа появлений герба. Найти его математическое ожидание, дисперсию, среднее квадратическое отклонение
 Скачать 26.48 Kb. Скачать 26.48 Kb.
|
|
Задача Монету подбрасывают три раза. Составить закон распределения случайной величины X - числа появлений герба. Найти его математическое ожидание, дисперсию, среднее квадратическое отклонение. Решение здесь по формуле бернулли с начало теорема Если вероятность p наступления события Α в каждом испытании постоянна, то вероятность того, что событие A наступит k раз в n независимых испытаниях, равна P(k.n)=Cn k *p^k*q^(n-k) то есть понятно что веротяность выпадение герба такое же что и выпадение другого , то есть аверс и реверс равны 1/2 или 50 на 50! всего как с уловия 5 раз и нам нужно их распределить ! по формуле бернулли получаем С 5 0 = 5!/0!(5-0)!= 1*2*3*4*5/1*1*2*3*4*5=1 то ест 1! С 5 1 =5!/1!(5-1)!=1*2*3*4*5/1*1*2*3*4=5 то есть 5 ! и так далее! P( 5 и 0)=1*1/2^0*1/2^5=1*1/32=1/32 P( 5 и 1)=5*1/2*1/2^4=5/2*1/16=5/32 P(5 и 6)=10*1/2^2*1/2^3=10/4*1/8=10/32 P(5 и 4)=10*1/2^3*1/2^2=10/8*1/4=10/32 P(5 и 5) =5*1/2^4*1/2=5/32 P( 5 и 5)=1*1/2^5*1/2^0=1/32 то есть вот и будет распрделение обычно ее в таблицу но можно и так здесь C n k число сочетаний число сочетаний по формуле чтобы понятней было Cлучайная величина Х принимает значения: 0; 1; 2; 3 Вероятность появления герба в одном испытании: p=1/2 Вероятность противоположного события · непоявление герба" q=1–(1/2)=1/2 Вероятность того, что при трех бросаниях монеты герб не появится ни разу po=C03·p0·q3=1·(1/2)3=1/8 p1=C13·p1·q2=3·(1/2)3=3/8 p2=C23·p2·q3=3·(1/2)3=3/8 p3=C33·p0·q3=1·(1/2)3=1/8 Закон распределения ( см. таблицу в приложении) M(X)=0·(1/8)+1·(3/8)+2·(3/8) + 3·(1/8)=12/8=3/2 И по формуле M(X)=np = 3·(1/2)=3/2 M(X2)=02·(1/8)+12·(3/8)+22·(3/8) + 32·(1/8)=24/8=3 D(X)=M(X2)–(M(X))2=3–(3/2)2=3–(9/4)=3/4 по формуле D(X)=npq=3·(1/2)·(1/2)=3/4 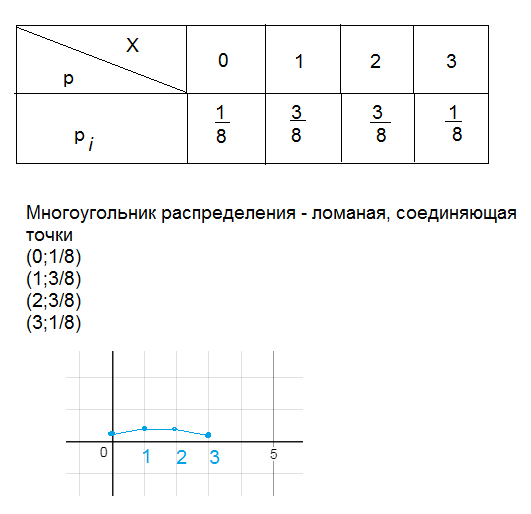 |
