Задача Найти общий интеграл дифференциального уравнения. (Ответ представить в виде.) 2. 4. 6
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
Расчетно-графическая работа по дисциплине «Математическое моделирование в задачах НГО. Методы математической физики» Задача 1. Найти общий интеграл дифференциального уравнения. (Ответ представить в виде 1.1. 1.3. 1.5. 1.7. 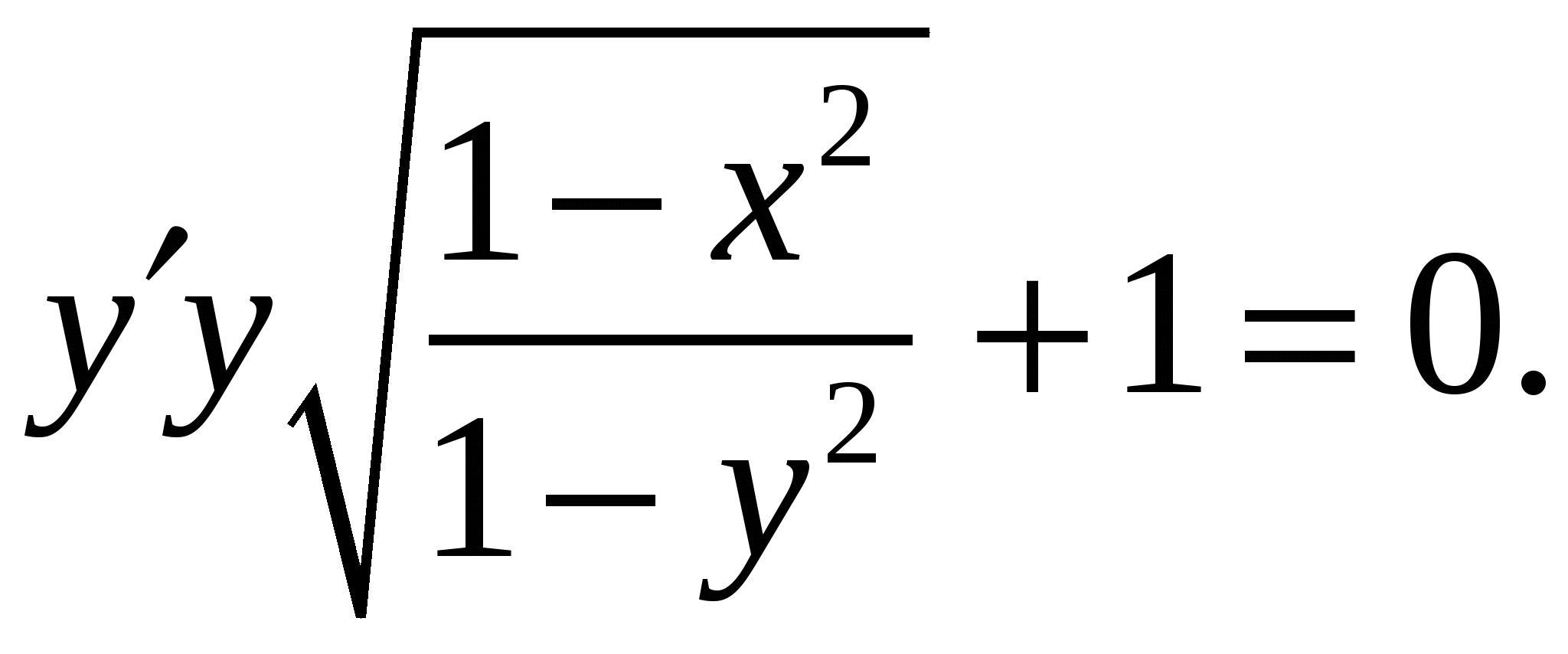 1.9. 1.11. 1.13. 1.15. 1.17. 1.19. 1.21. 1.23. 1.25. Задача 2. Найти общий интеграл дифференциального уравнения. 2.1. 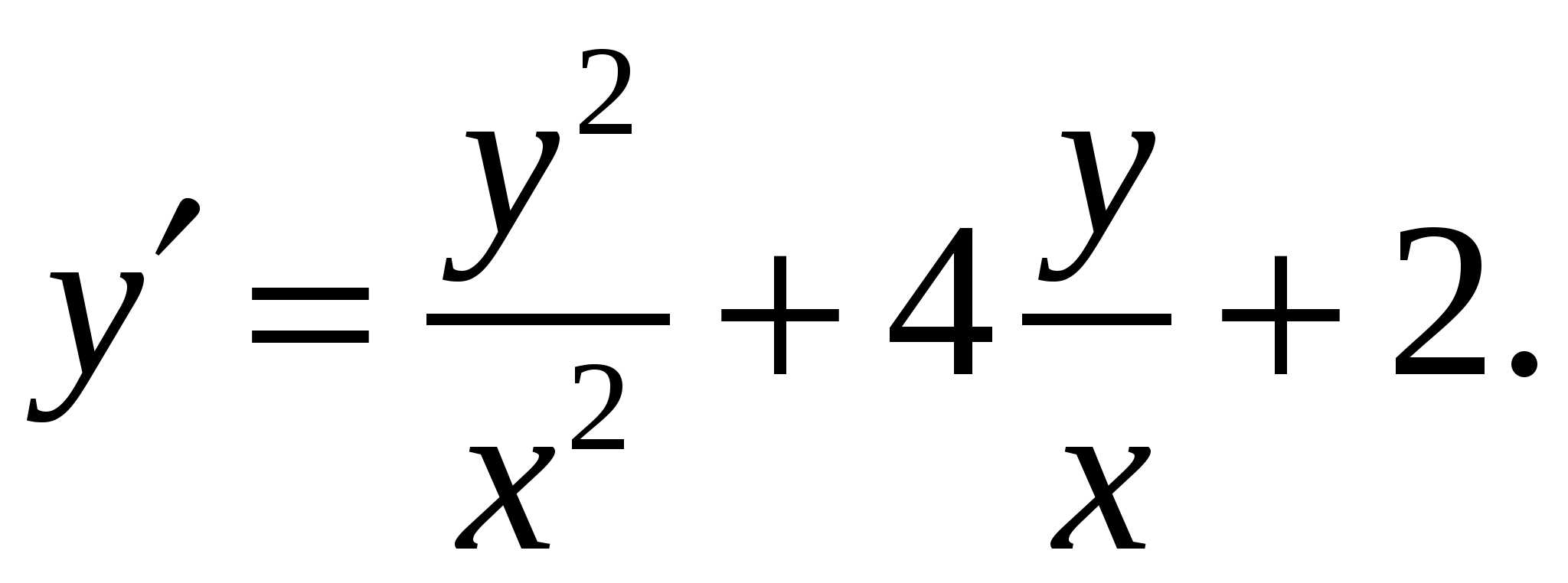 2.2. 2.2. 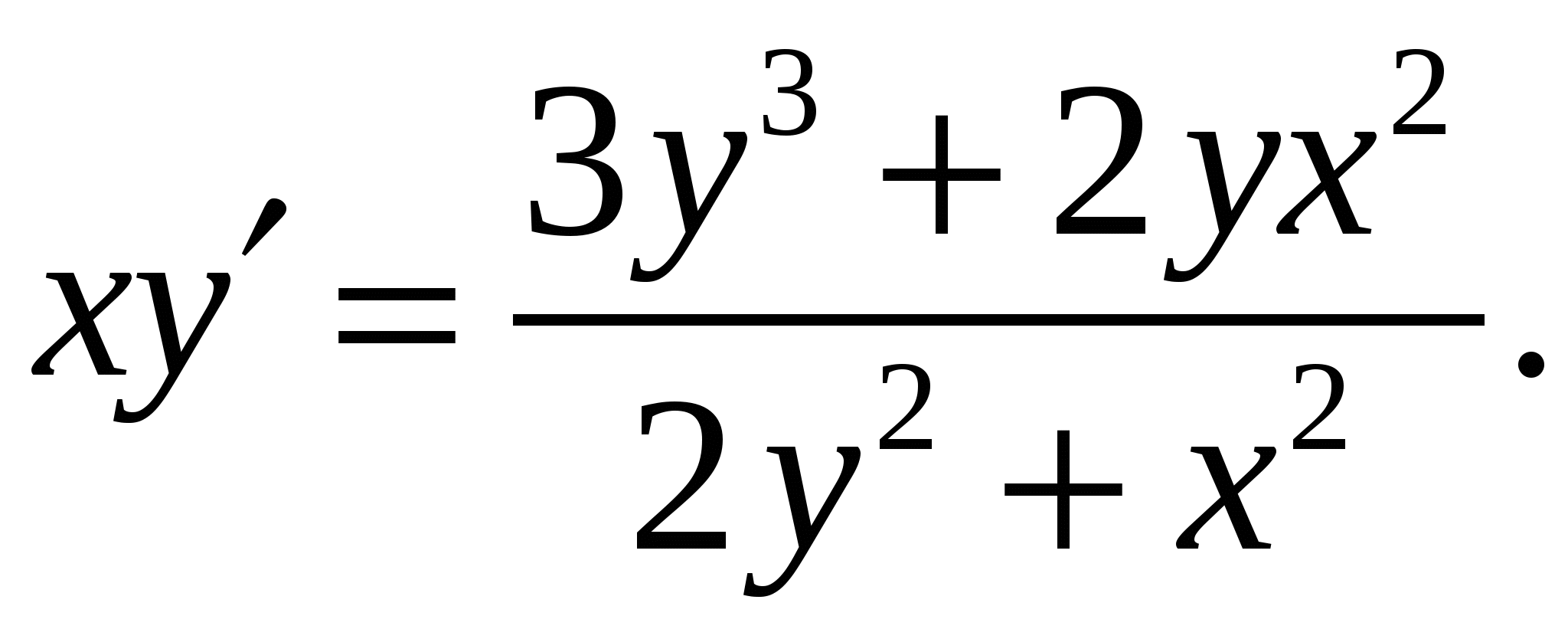 2.3. 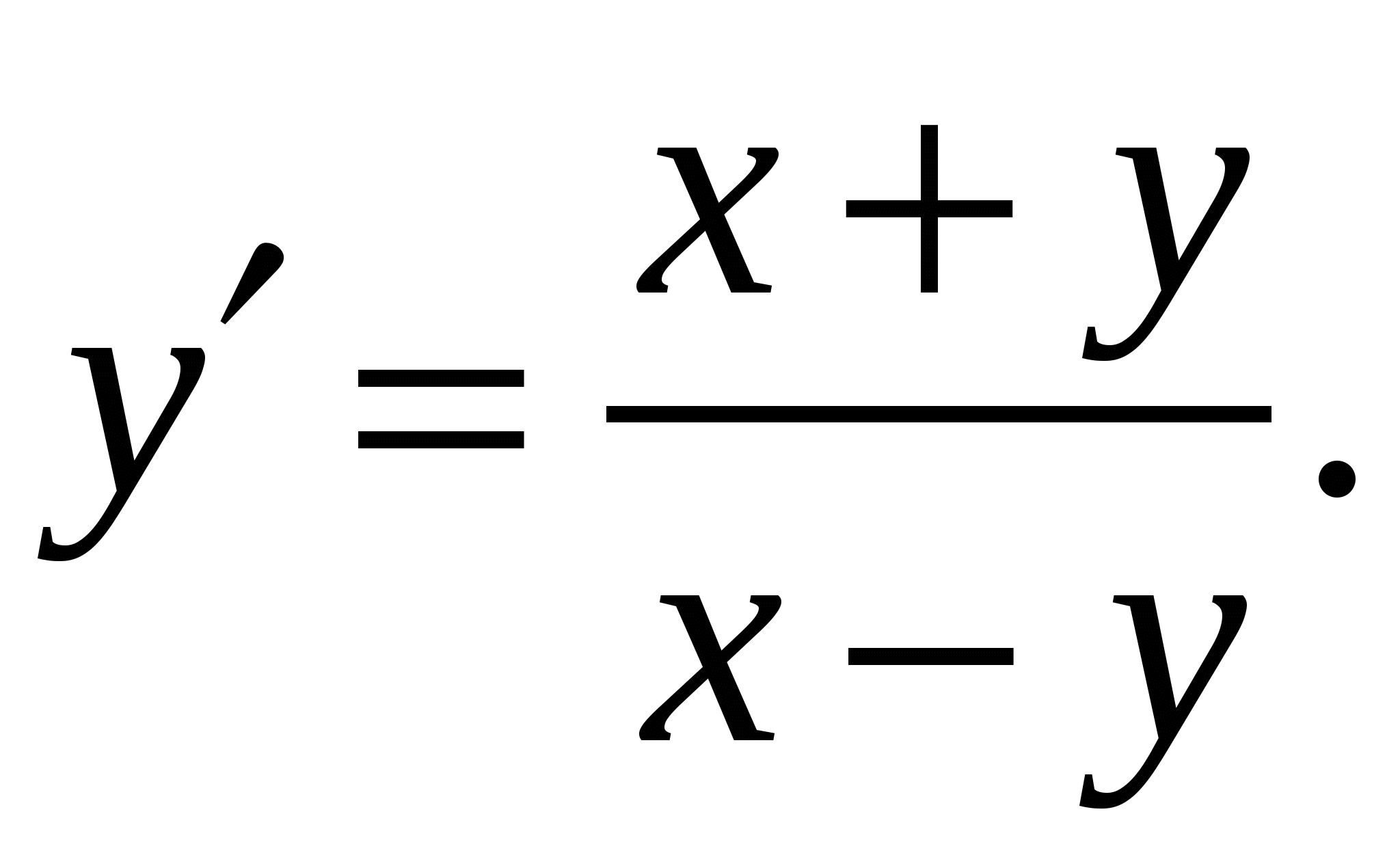 2.4. 2.4. 2.5. 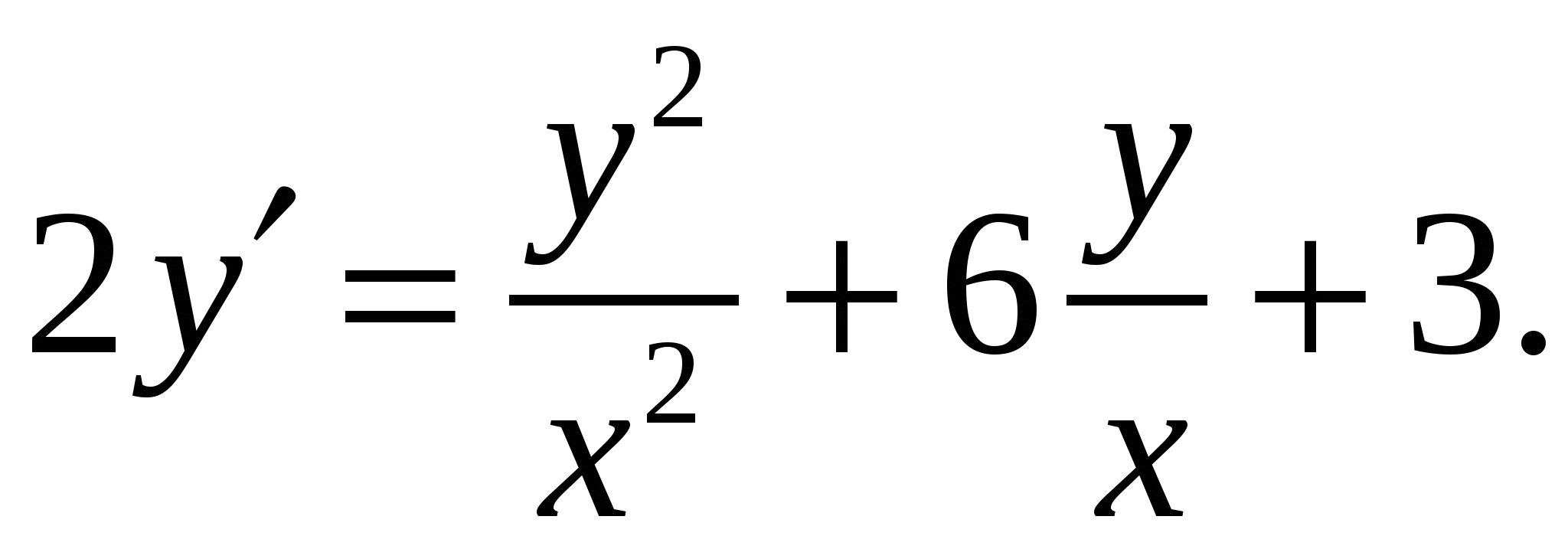 2.6. 2.6. 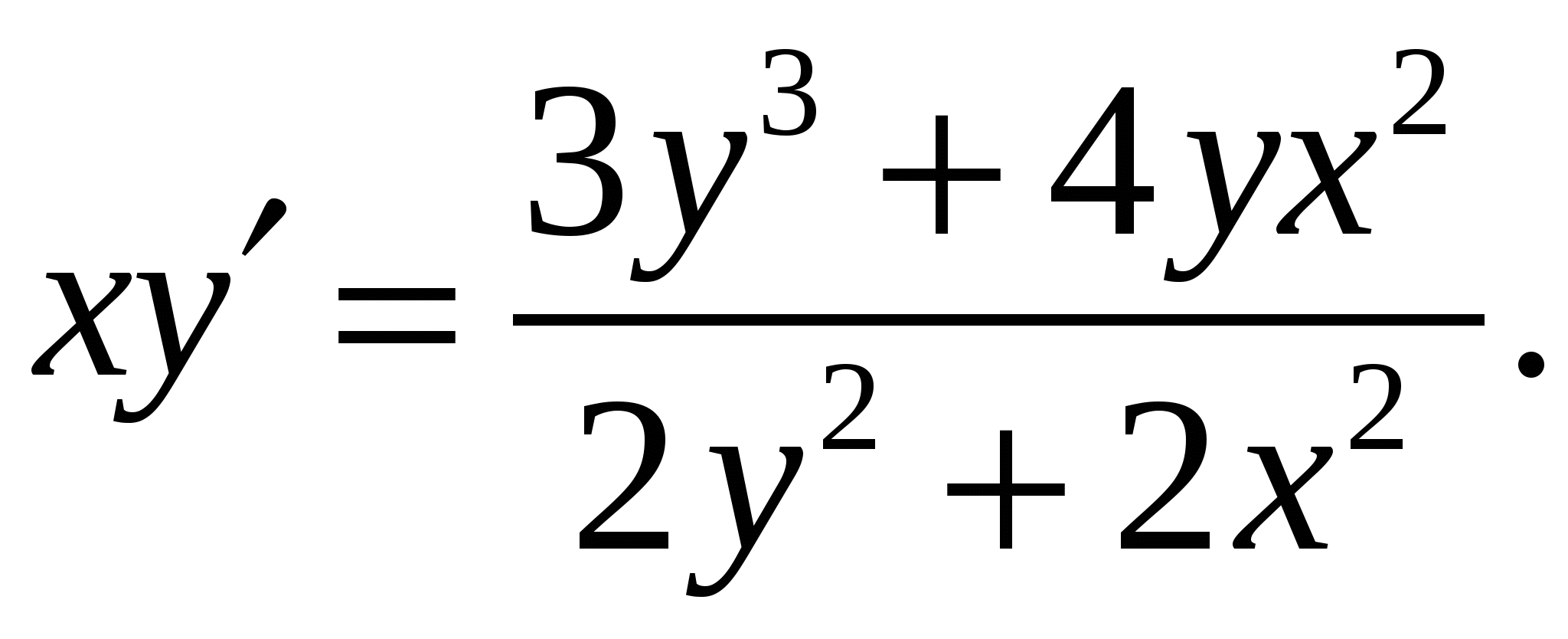 2.7. 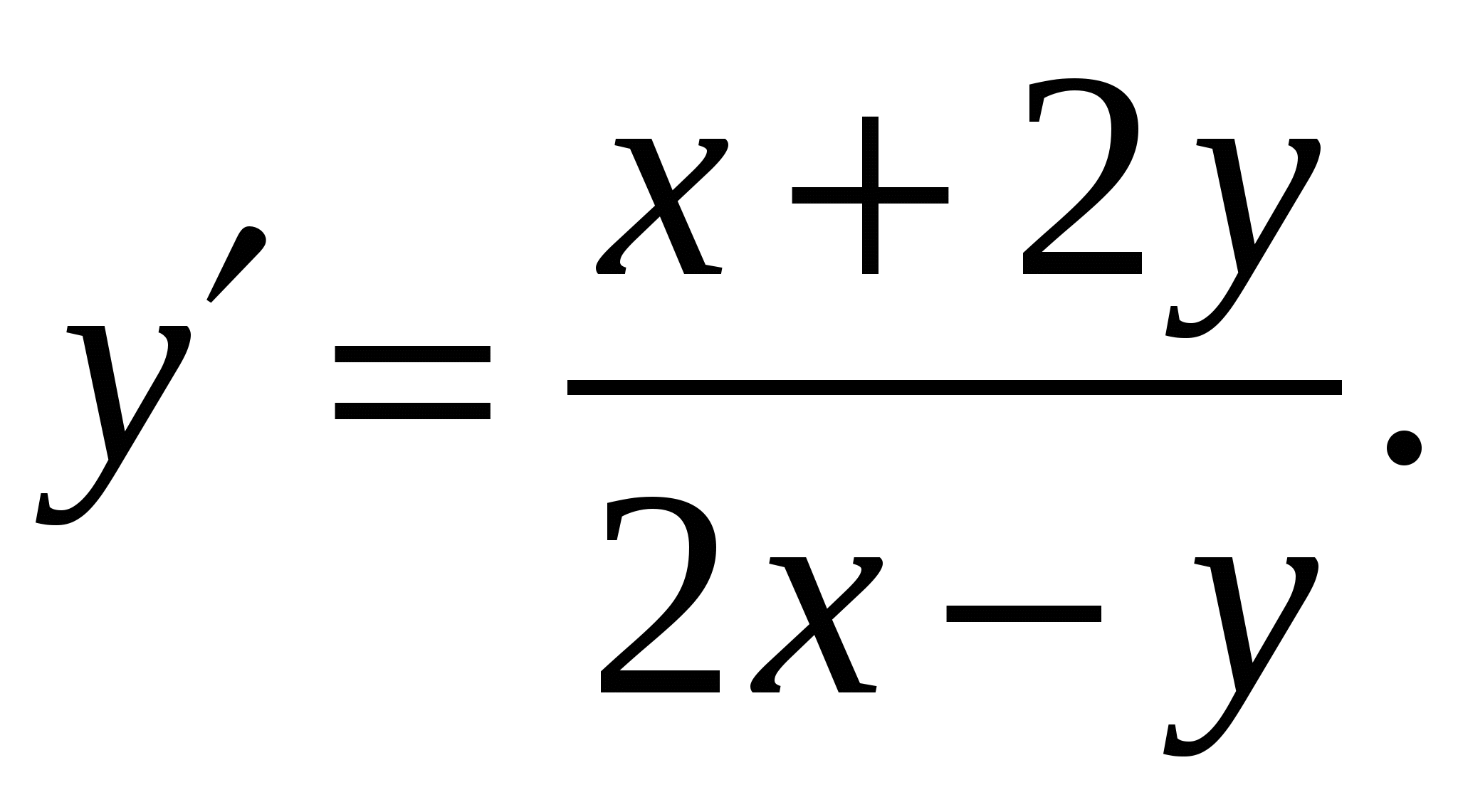 2.8. 2.8. 2.9. 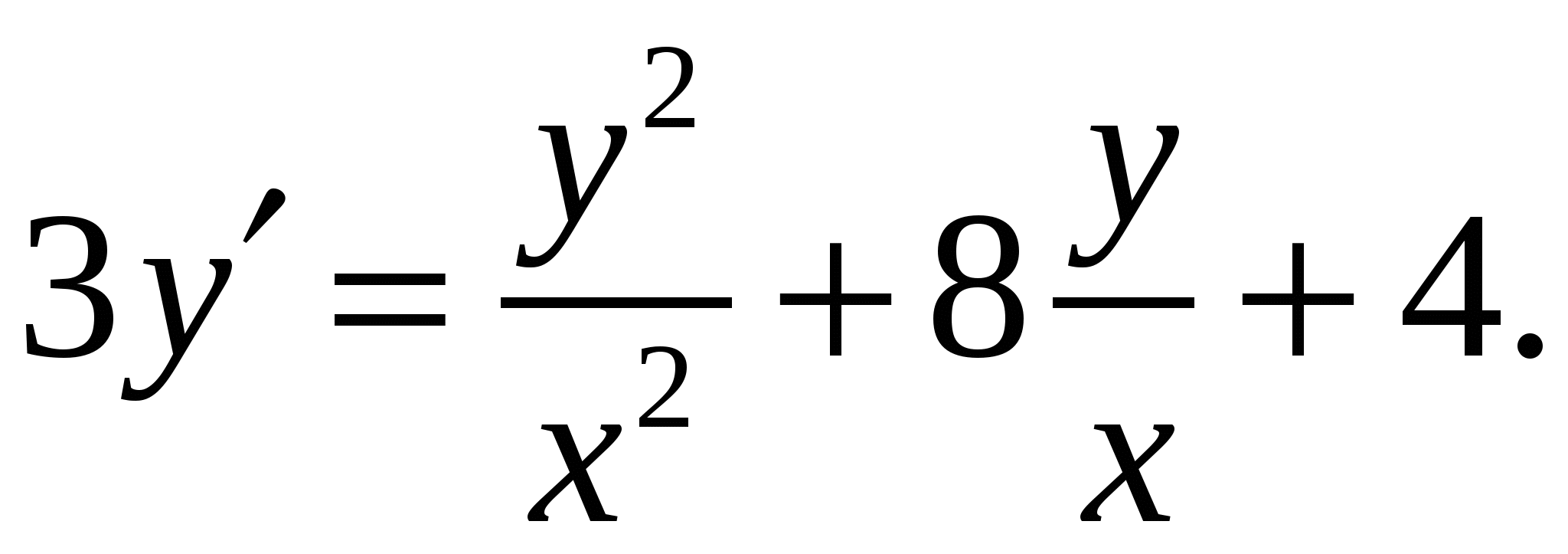 2.10. 2.10. 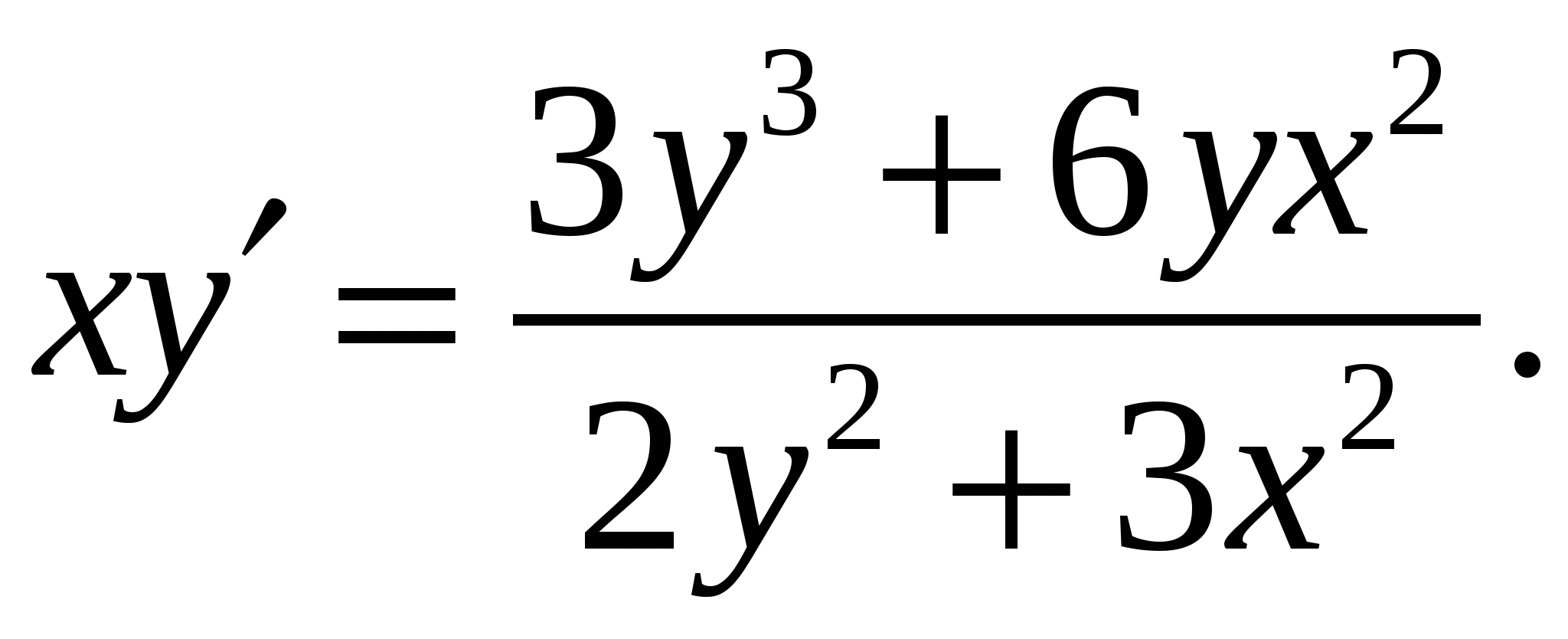 2.11. 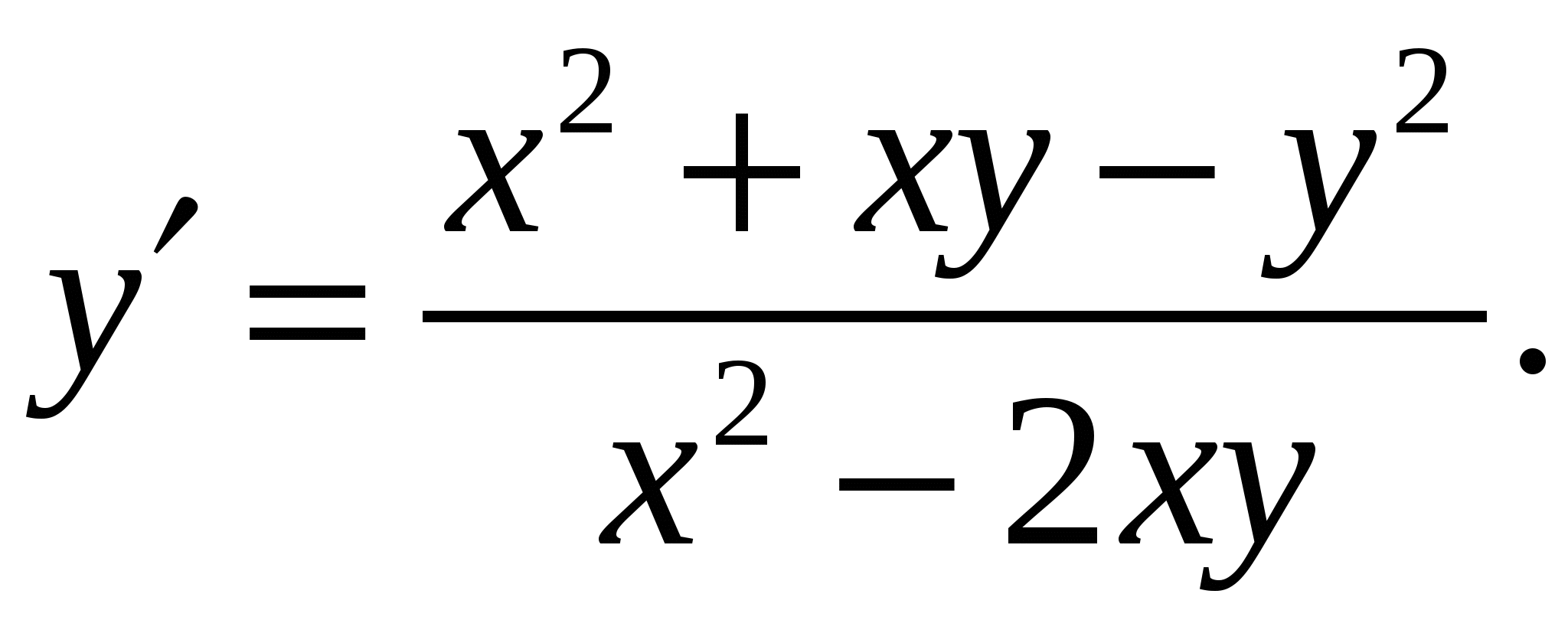 2.12. 2.12. 2.13. 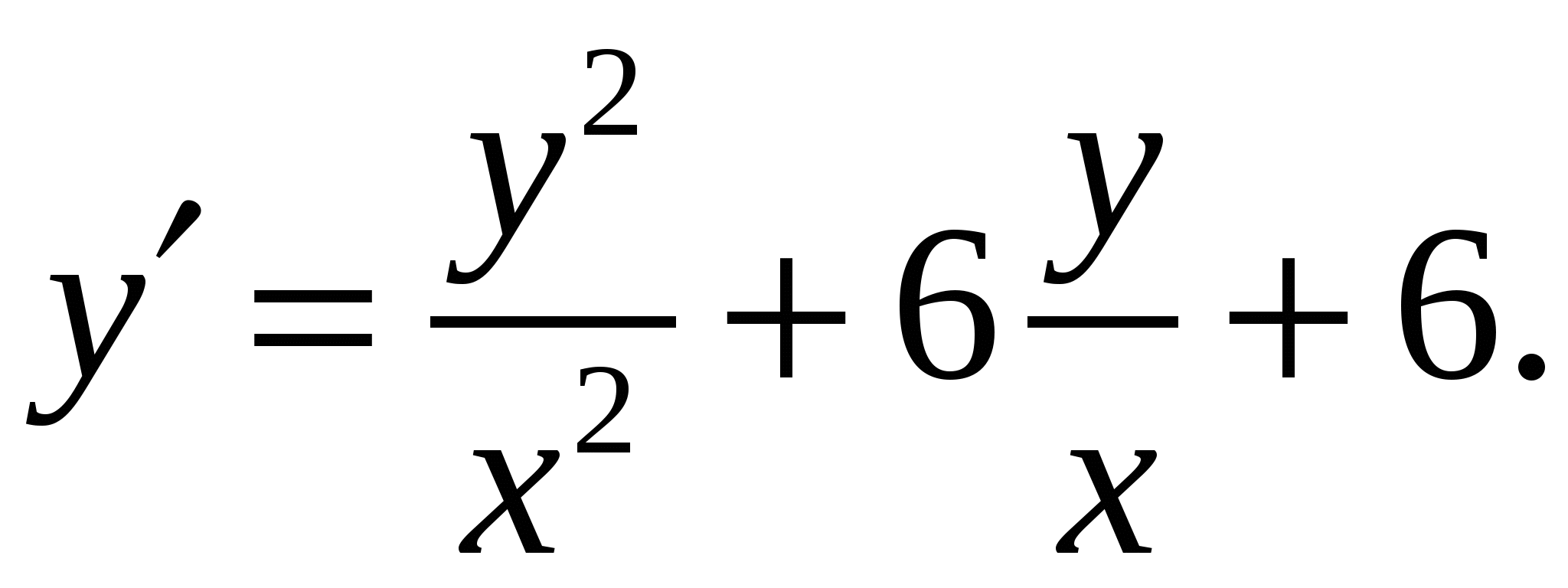 2.14. 2.14. 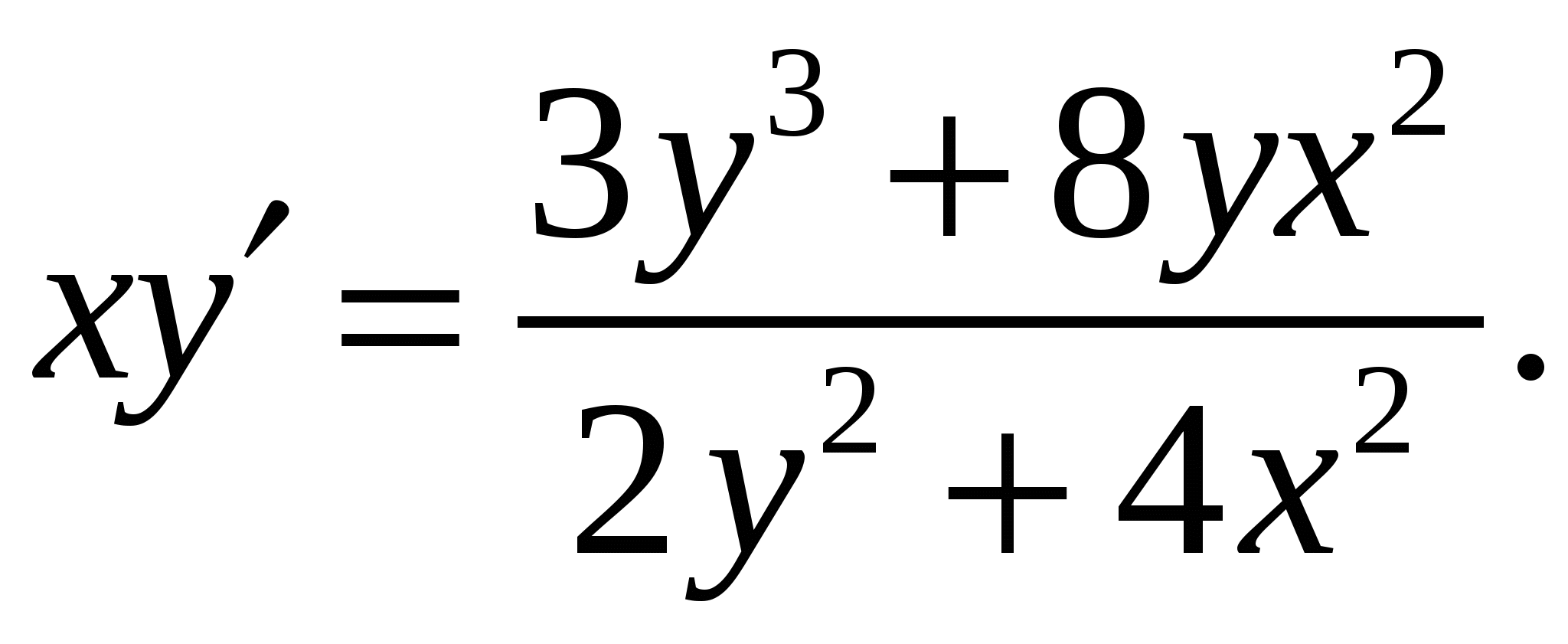 2.15. 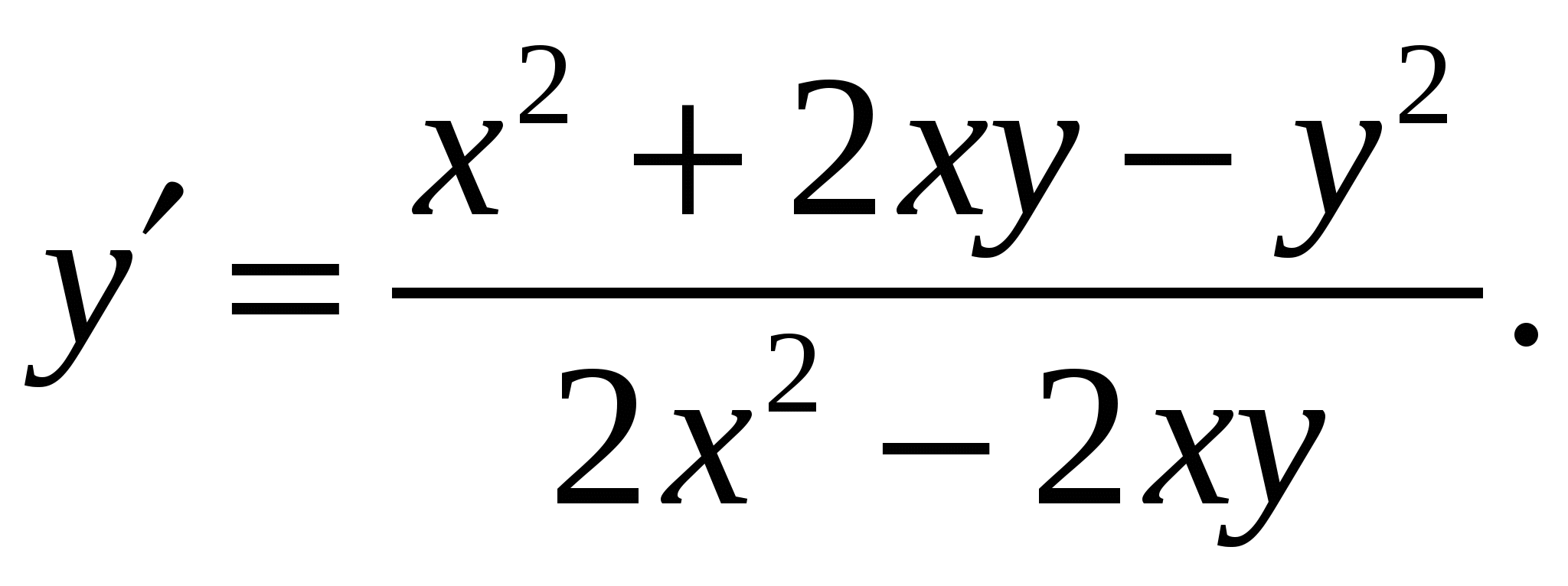 2.16. 2.16. 2.17. 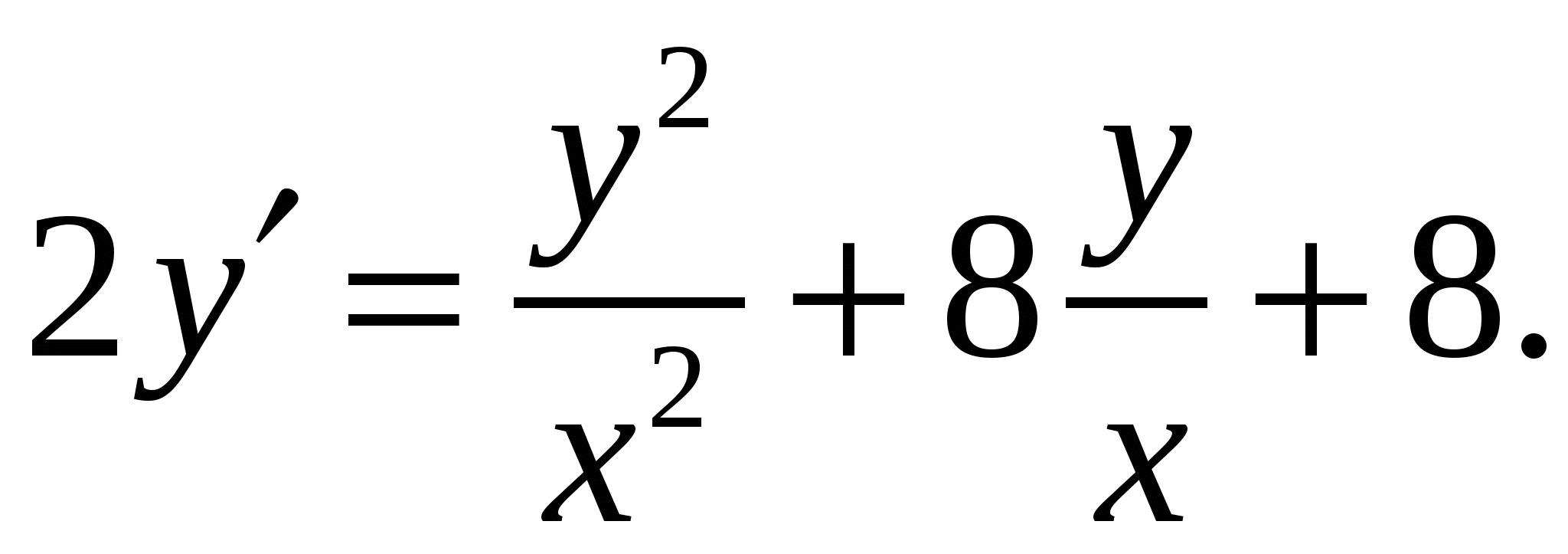 2.18. 2.18. 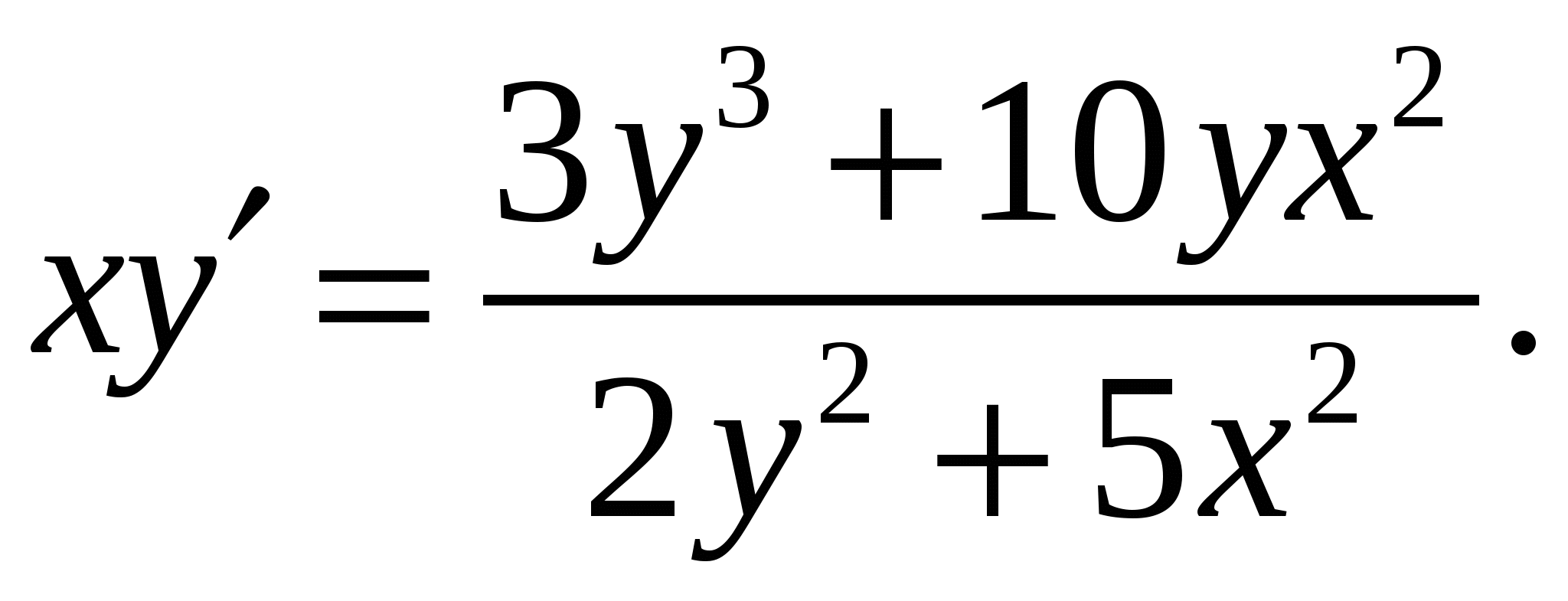 2.19. 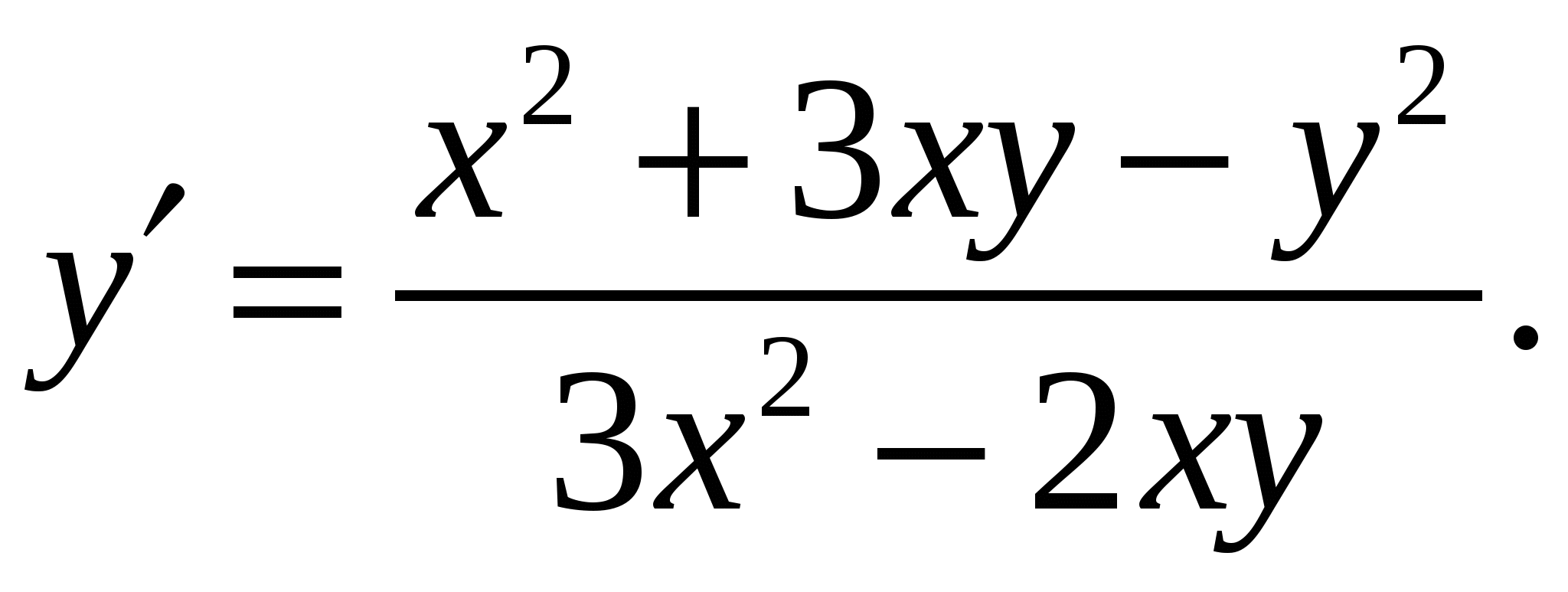 2.20. 2.20. 2.21. 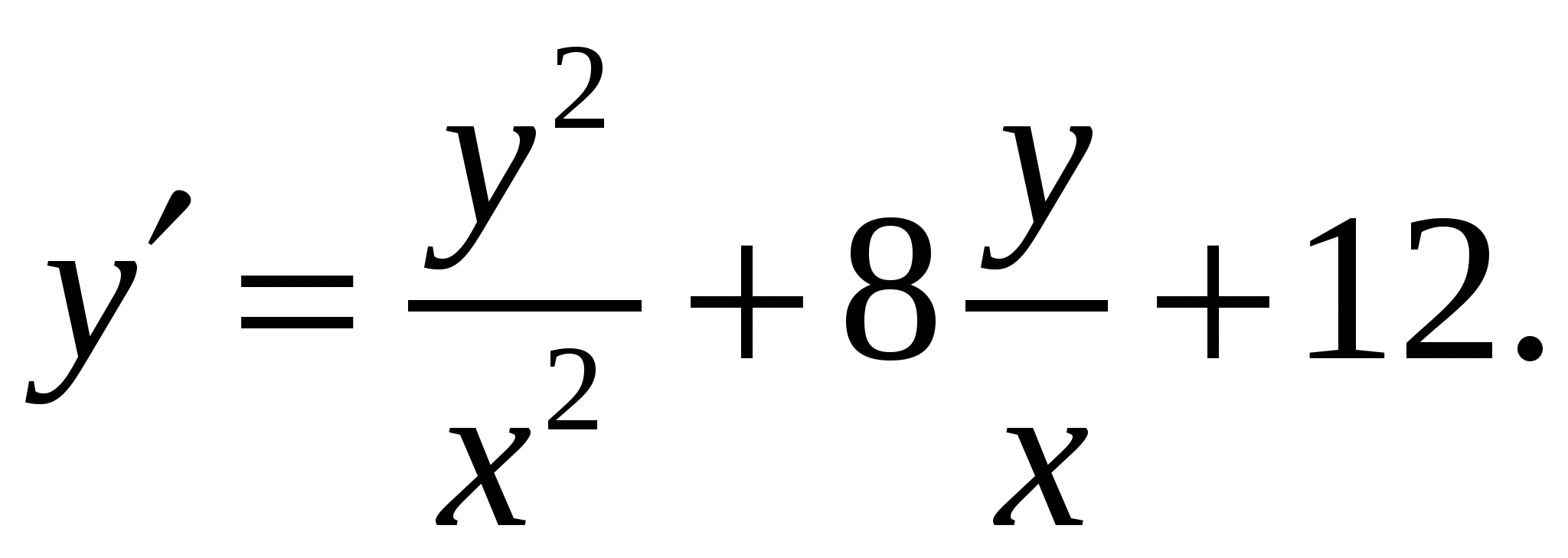 2.22. 2.22. 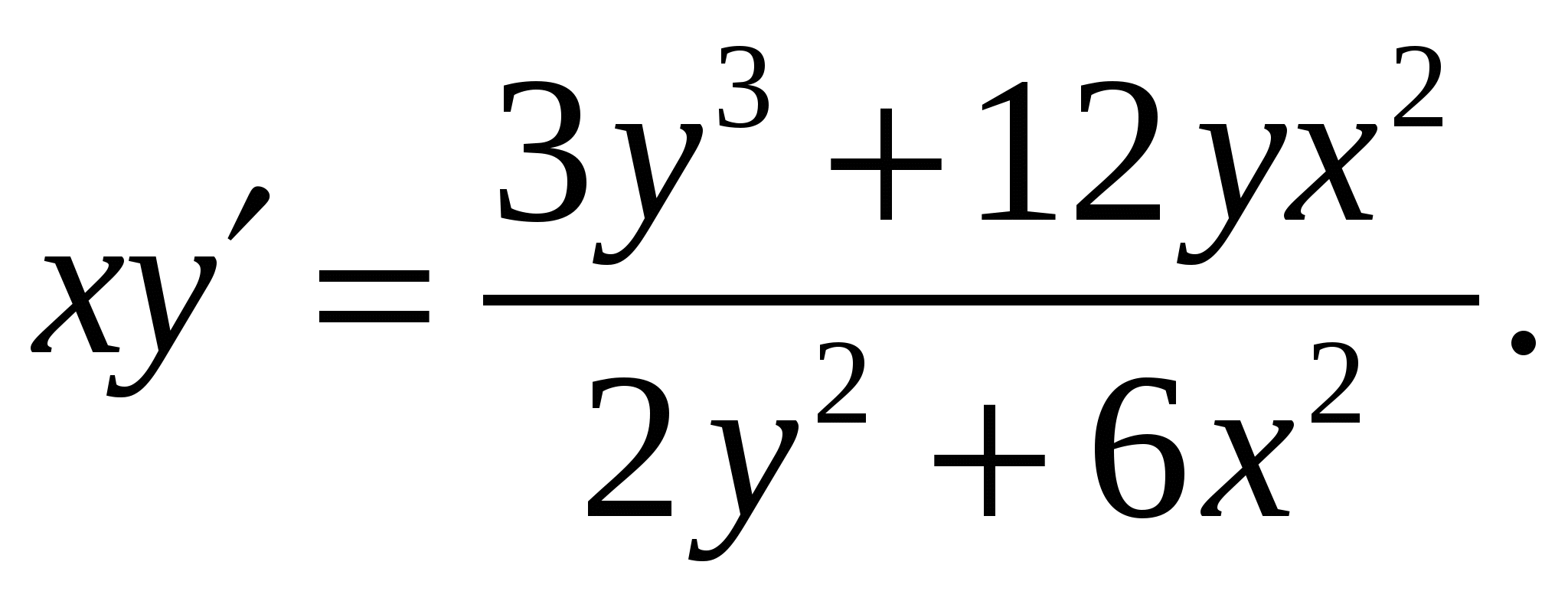 2.23. 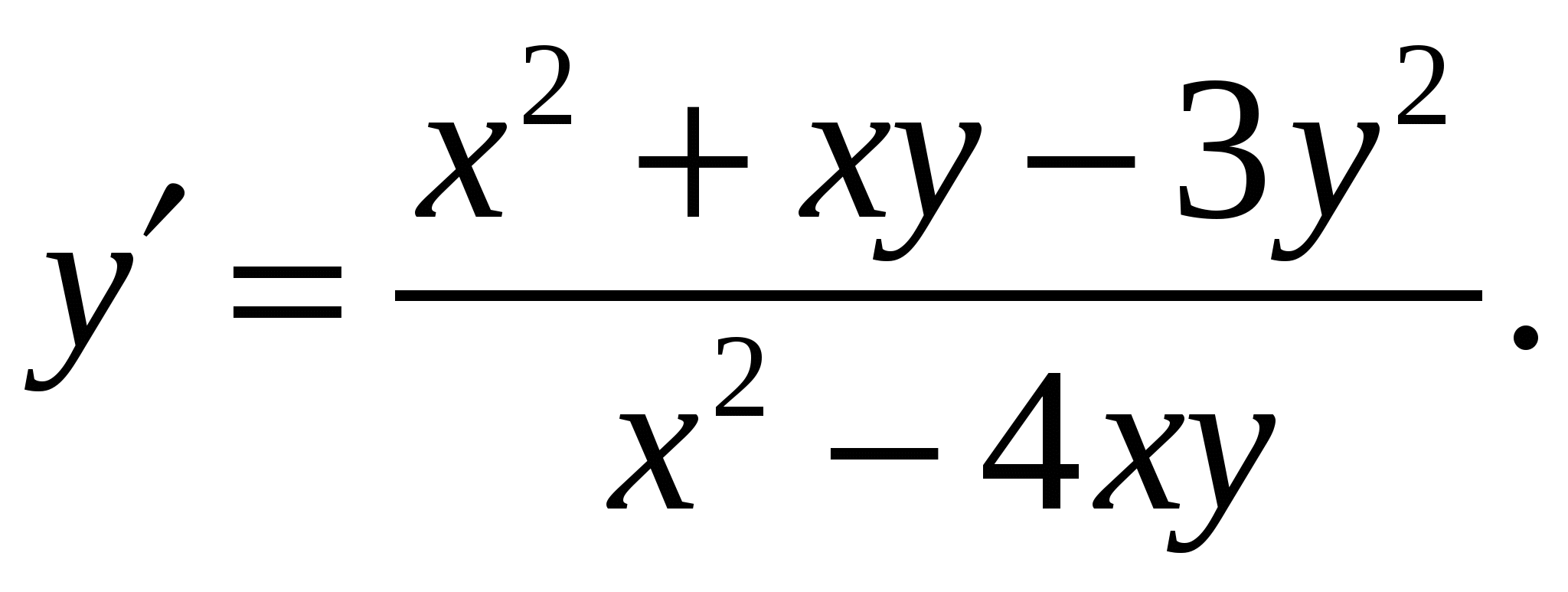 2.24. 2.24. 2.25. 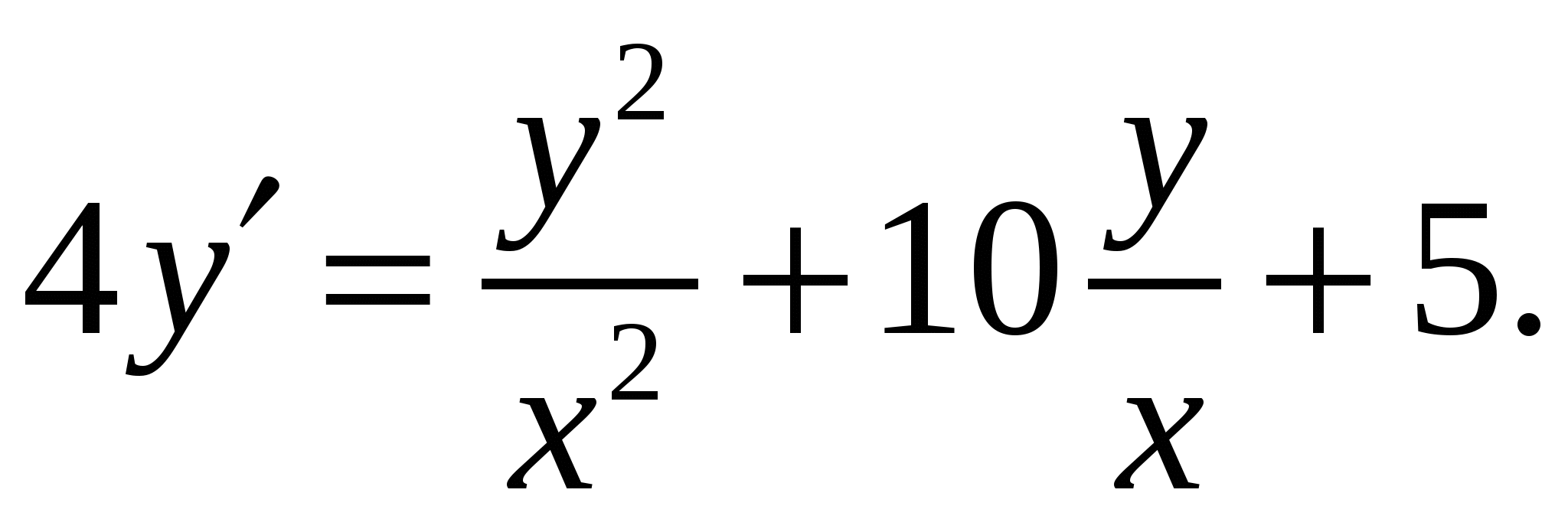 Задача 3. Найти решение задачи Коши для обыкновенного дифференциального уравнения первого порядка. 3.1. 3.3. 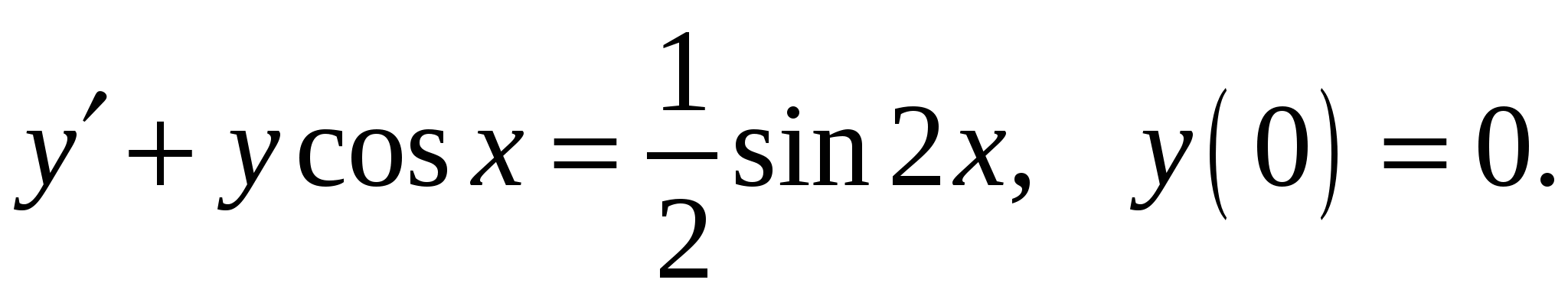 3.4. 3.4. 3.5. 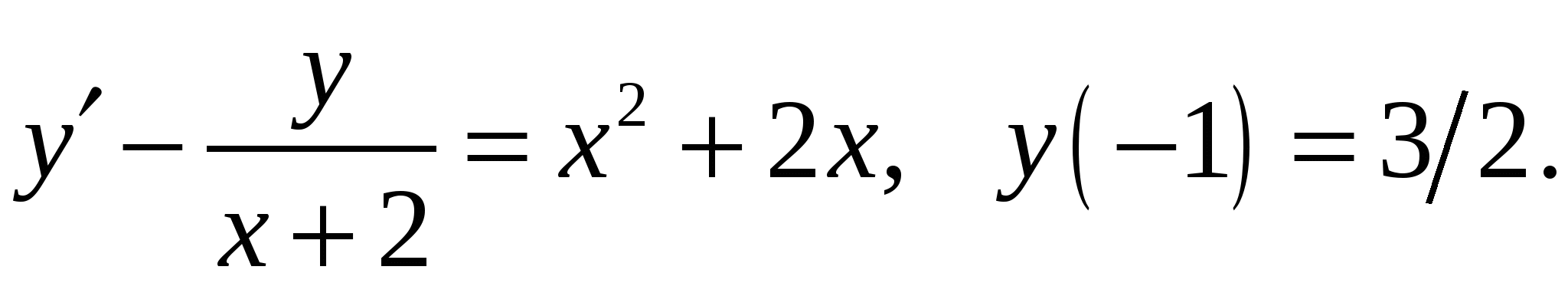 3.6. 3.6. 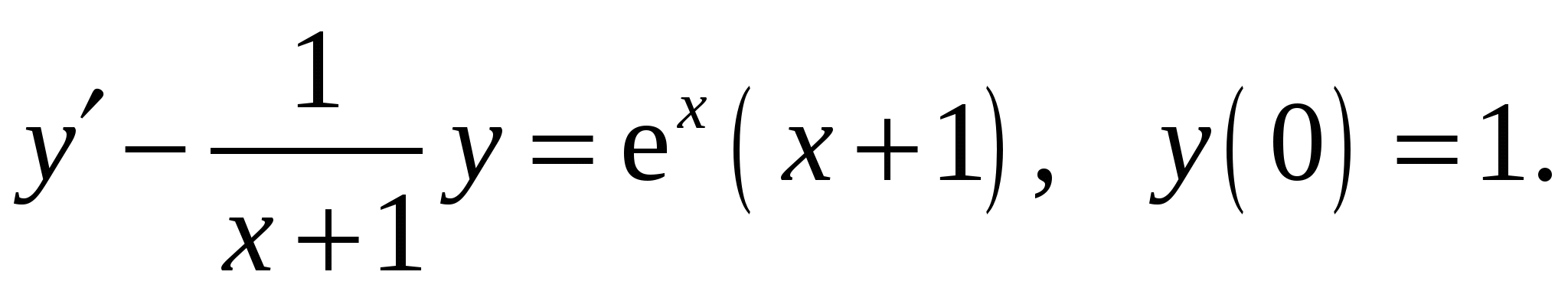 3.7.  3.8. 3.8. 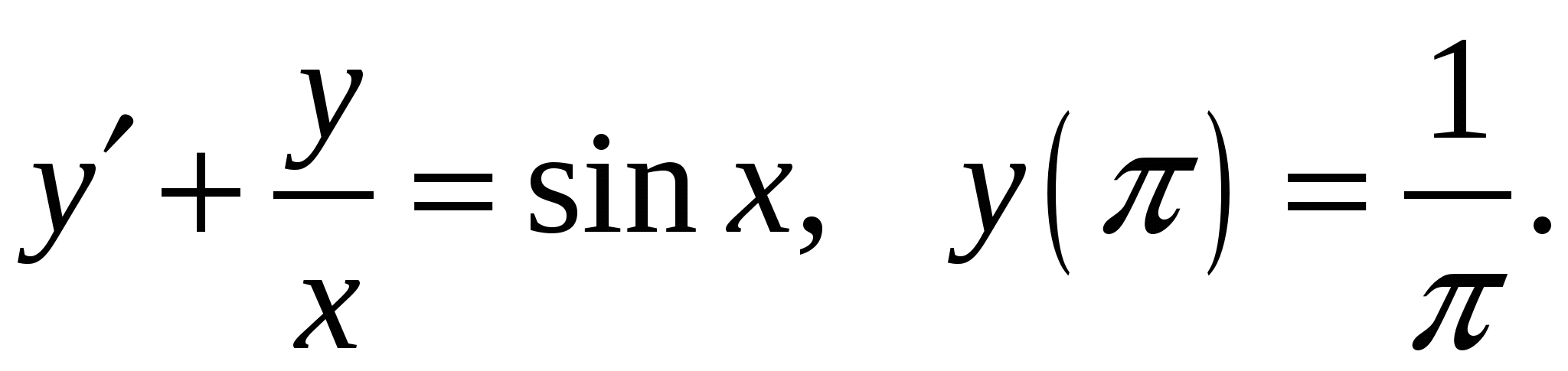 3.9. 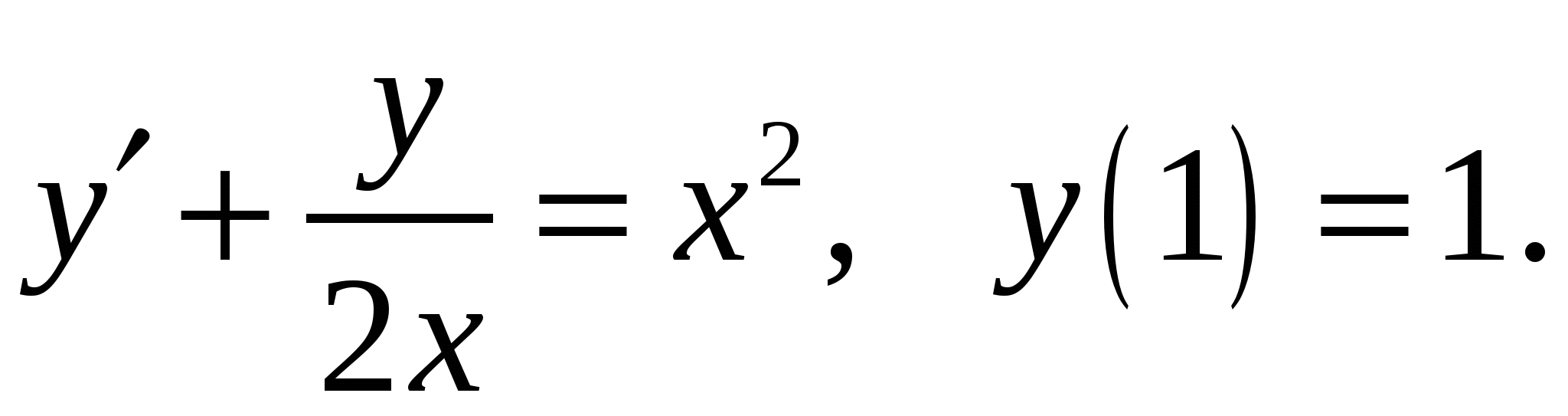 3.10. 3.10. 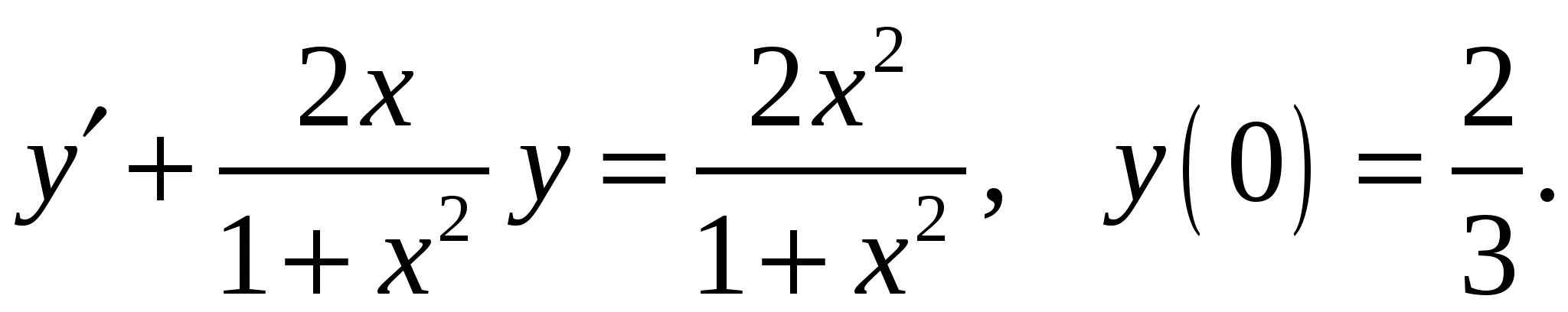 3.11. 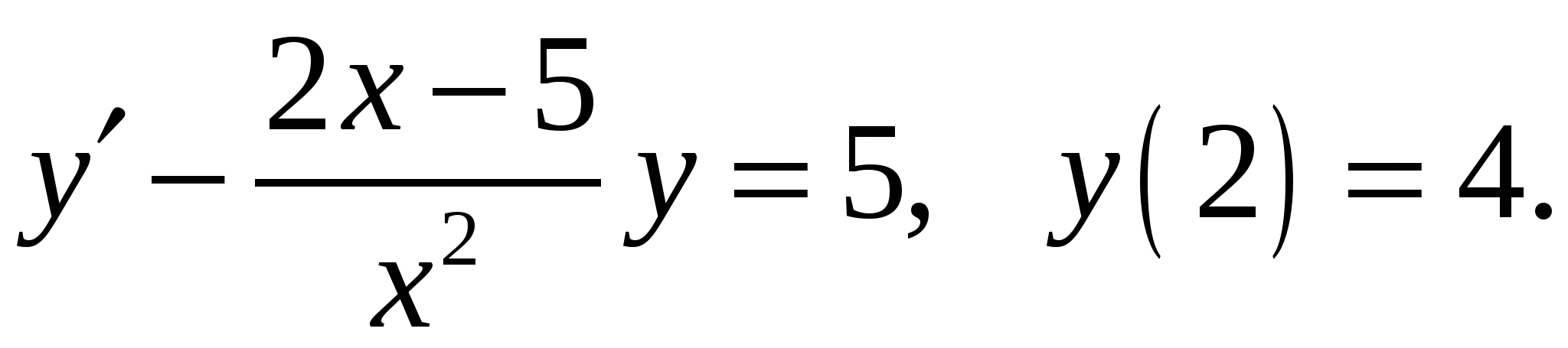 3.12. 3.12. 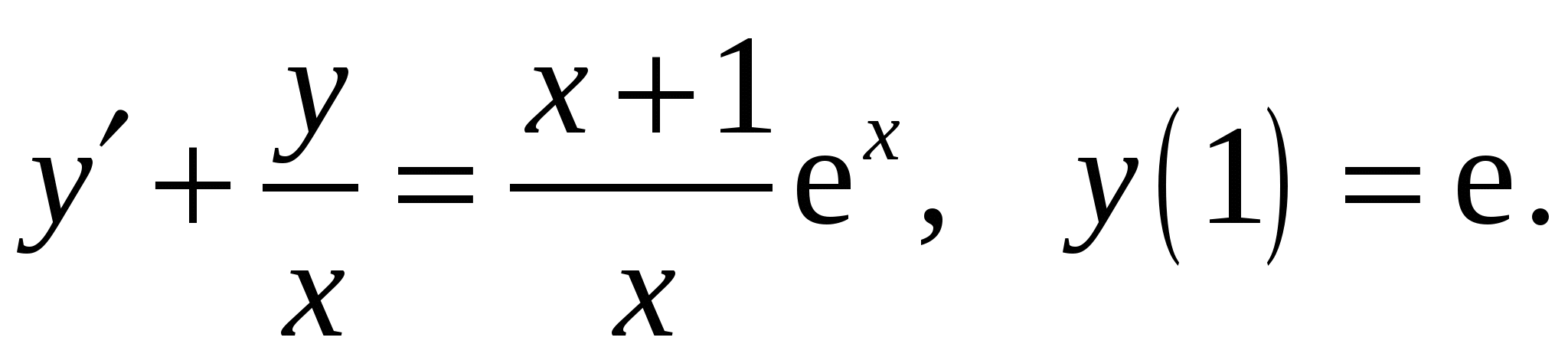 3.13. 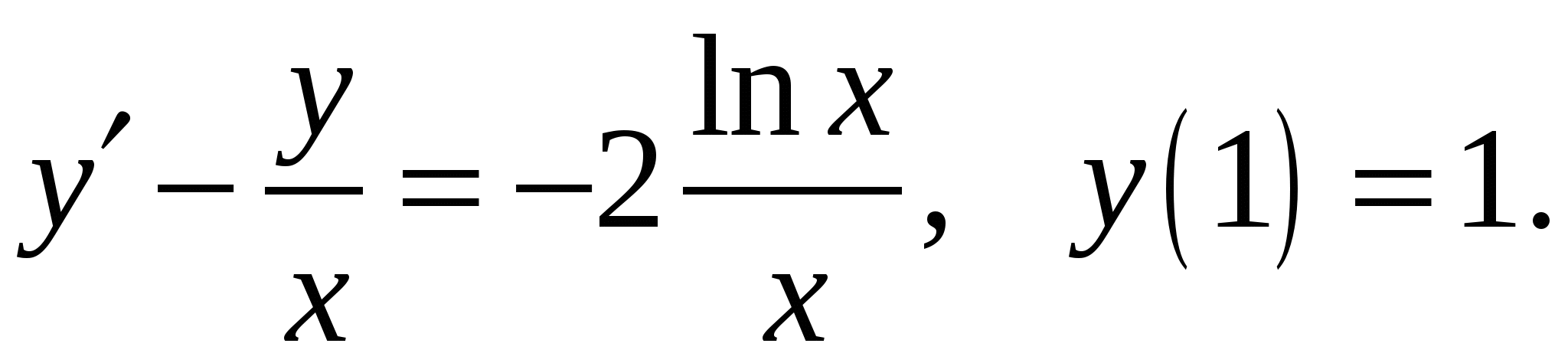 3.14. 3.14. 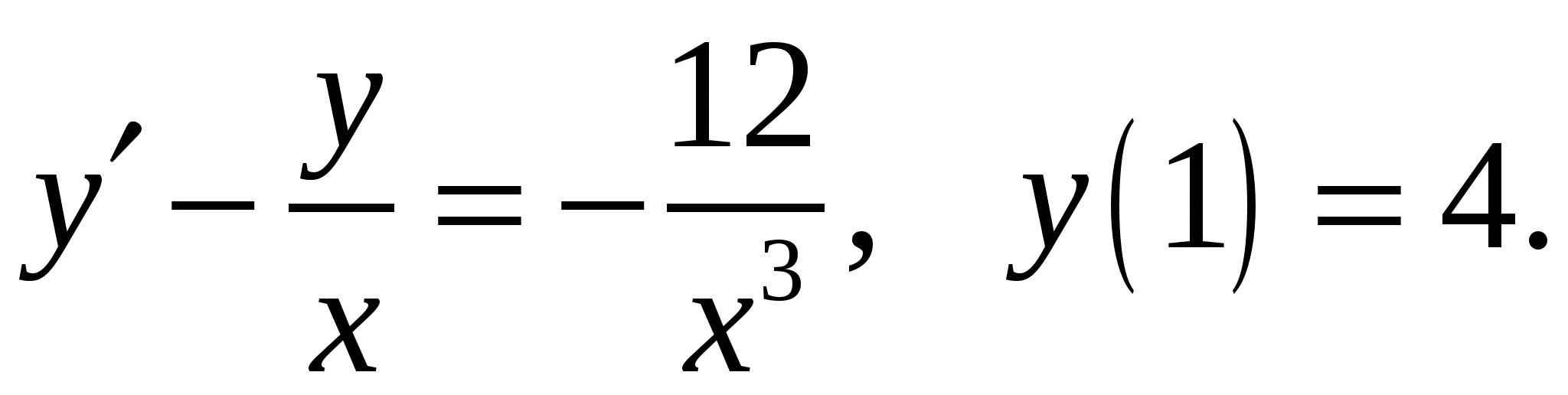 3.15. 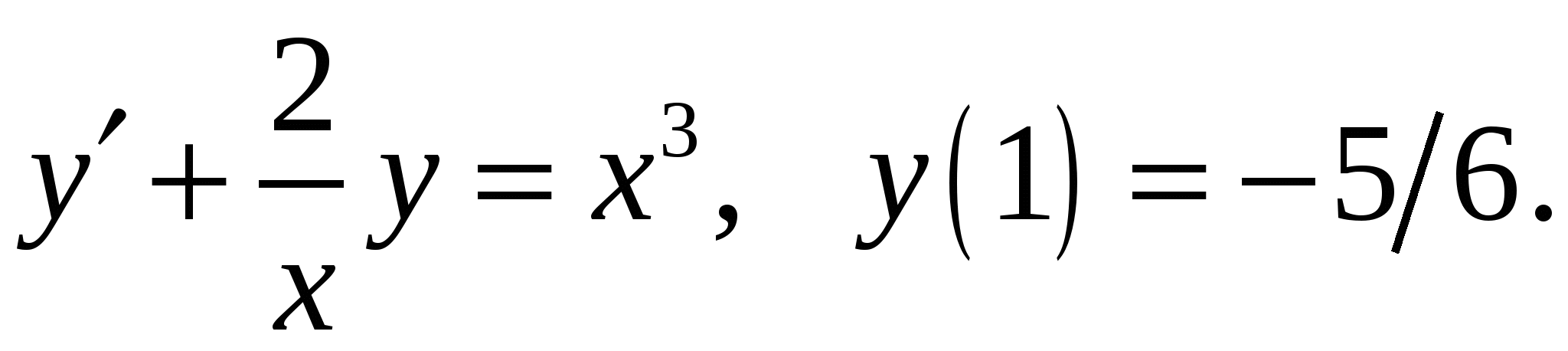 3.16. 3.16. 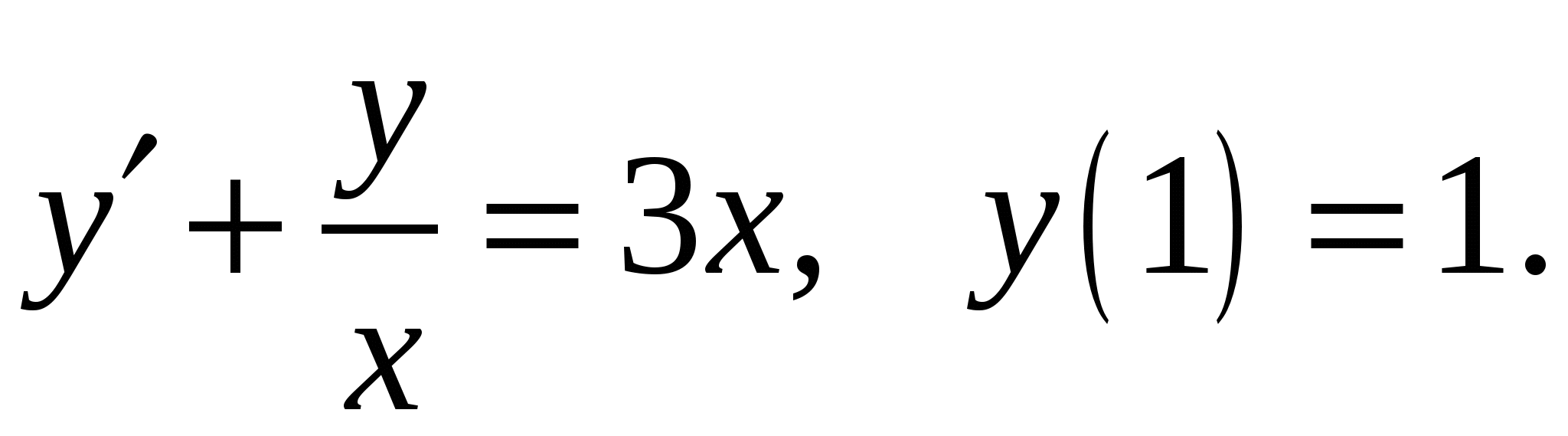 3.17. 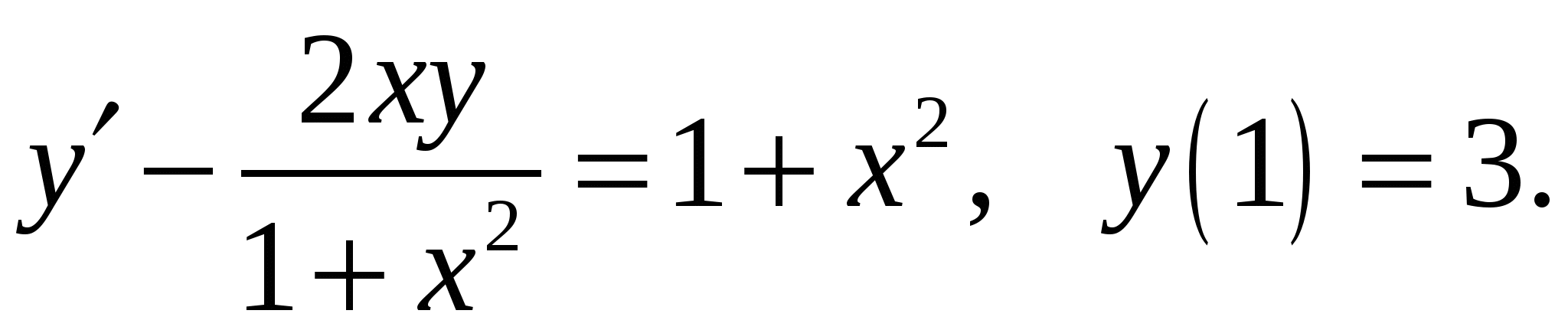 3.18. 3.18. 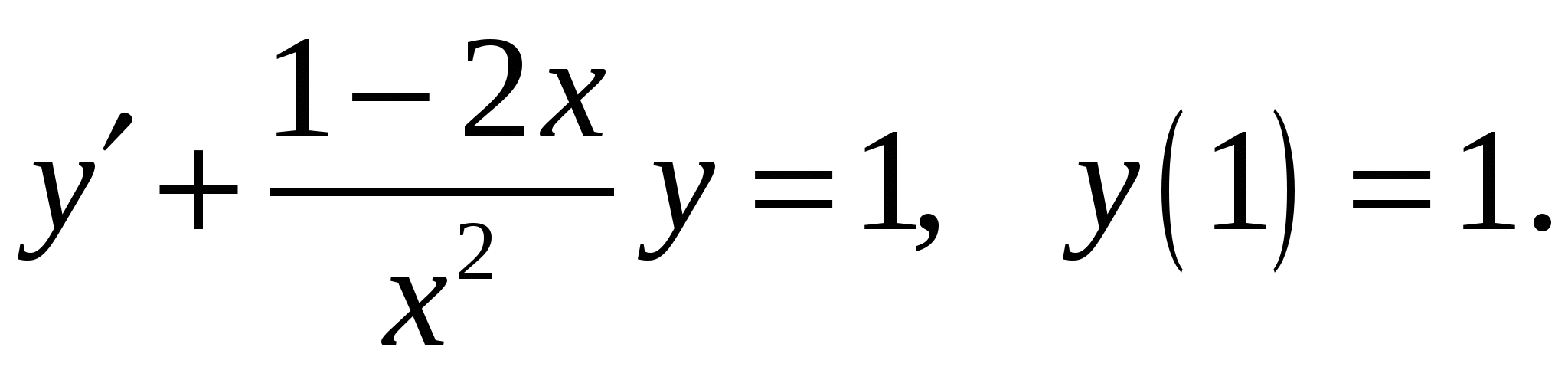 3.19. 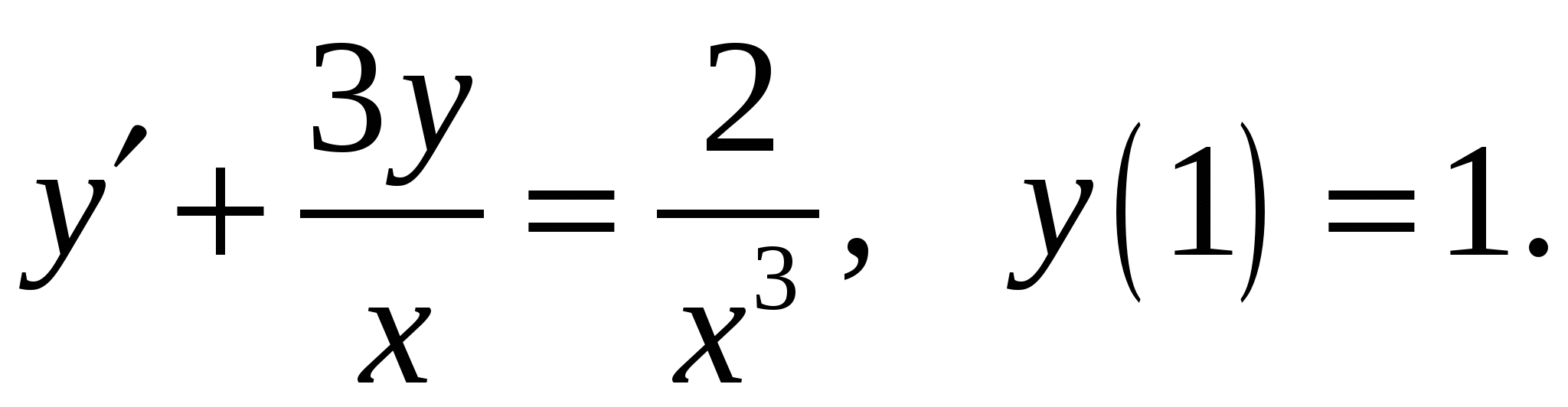 3.20. 3.20. 3.21. 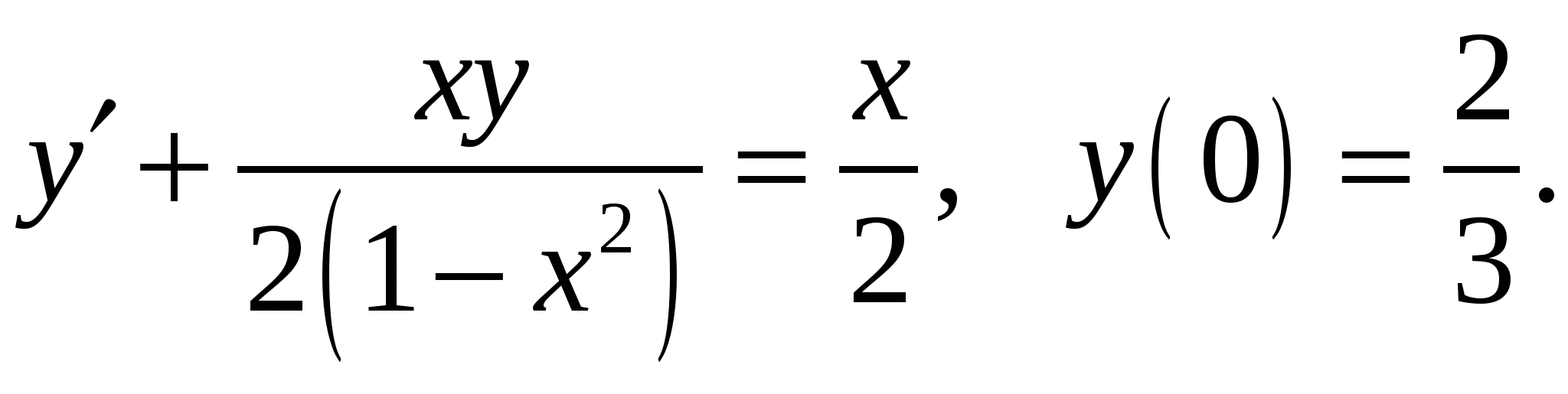 3.22. 3.22. 3.23. 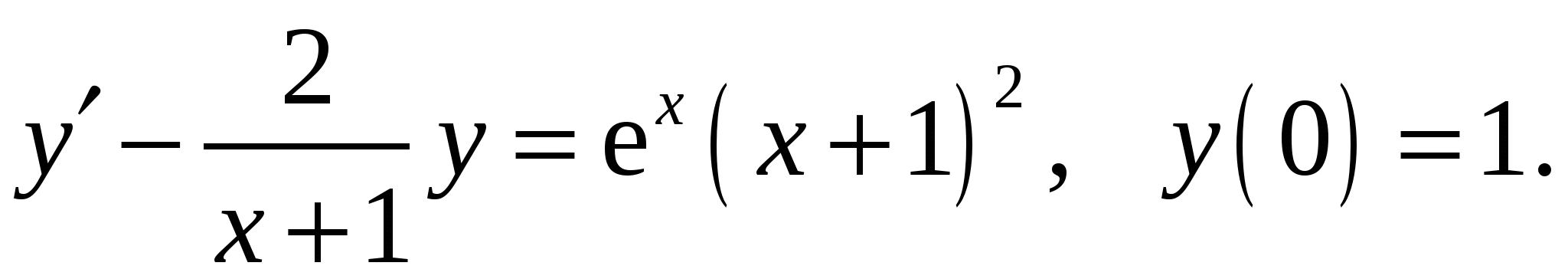 3.24. 3.24. 3.25. Задача 4. Найти общее решение линейного неоднородного дифференциального уравнения с правой частью специального вида. 4.1. 4.3. 4.5. 4.7. 4.9. 4.11. 4.13. 4.15. 4.17. 4.19. 4.21. 4.23. 4.25. Задача 5 (Задача Штурма - Лиувилля). Найти все значения 5.1. 5.3. 5.5. 5.7. 5.9. 5.11. 5.13. 5.15. 5.17. 5.19. 5.21. 5.23. 5.25. Задача 6. Найти общее решение дифференциального уравнения в частных производных первого порядка: 6.1. а) 6.2. а) 6.3. а) 6.4. а) 6.5. а) 65.6. а) 6.7. а) 6.8. а) 6.9. а) 6.10. а) 6.11. а) 6.12. а) 6.13. а) 6.14. а) 6.15. а) 6.16. а) 6.17. а) 6.18. а) 6.19. а) 6.20. а) 6.21. а) 6.22. а) 6.23. а) 6.24. а) 6.25. а) Задача 7. Привести к каноническому виду, найти общее решение дифференциального уравнения и сделать проверку подстановкой: 7.1. 7.3. 7.5. 7.7. 7.9. 7.11. 7.13. 7.15. 7.17. 7.19. 7.21. 7.23. 7.25. Задача 8. Найти решение задачи Дирихле для уравнения Лапласа 8.1. а) 8.2. а) 8.3. а) 8.4. а) 8.5. а) 8.6. а) 8.7. а) 8.8. а) 8.9. а) 8.10. а) 8.11. а) 8.12. а) 8.13. а) 8.14. а) 8.15. а) 8.16. а) 8.17. а) 8.18. а) 8.19. а) 8.20. а) 8.21. а) 8.22. а) 8.23. а) 8.24. а) 8.25. а) Задача 9. Решить первую смешанную (начально-граничную) задачу для волнового уравнения. 9.1. 9.2. 9.3. 9.4. 9.5. 9.6. 9.7. 9.8. 9.9. 9.10. 9.11. 9.12. 9.13. 9.14. 9.15. 9.16. 9.17. 9.18. 9.19. 9.20. 9.21. 9.22. 9.23. 9.24. 9.25. |
