ІВК. Асиметричне криптоперетворення. Задача Нехай p 20 і q 11. Побудувати пару ( ) для rsa криптоалгоритму, якщо p , q Розв ' язок задасі
 Скачать 17.11 Kb. Скачать 17.11 Kb.
|
|
Друга задача Нехай P=20 і Q=11.Побудувати пару ( 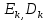 ) для RSA криптоалгоритму, якщо P= ) для RSA криптоалгоритму, якщо P=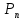 , Q= , Q=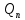 Розв'язок задасі: Знаходимо модуль перетворення та значення функції Ойлера 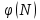 N= 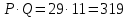 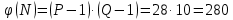 Порівняння виду 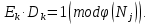 Запишемо у вилгляді Діафантового рівняння 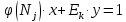 Вибравши випадково 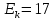 ключ, взаєпростий з функцією Ойлера, тобто ключ, взаєпростий з функцією Ойлера, тобто 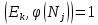 , маємо , маємо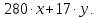 Тепер подамо a/b у вигляді ланцюгового дробу: 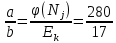 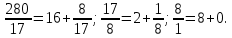 Таким чином µ=2 Розрахуємо значення 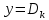 використовуючи співвідношення використовуючи співвідношення 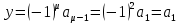 Знаходимо рекурентно значення 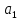 : :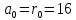 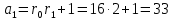 Підставивши значення 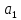 маємо маємо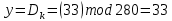 Таким чином пара 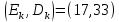 складає RSA ключову пару. складає RSA ключову пару.Перевірка: Підставивши значення ключів 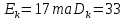 , маємо , маємо 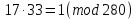 Асиметричне криптоперетворення — ефективні системи криптографічного захисту даних, які також називають криптосистемами з відкритим ключем. В таких системах для зашифровування даних використовують один ключ, а для розшифровування — інший (звідси і назва — асиметричні). Перший ключ є відкритим і може бути опублікованим для використання усіма користувачами системи, які шифрують дані. Розшифровування даних за допомогою відкритого ключа неможливе. Для розшифровування даних отримувач зашифрованої інформації використовує другий ключ, який є секретним (закритим). Зрозуміло, що ключ розшифровування не може бути визначеним з ключа зашифровування. Число n {\displaystyle n\,} називається модулем, а числа {\displaystyle e\,}e і {\displaystyle d\,}d — відкритою й секретною експонентами, відповідно. Пари чисел {\displaystyle (n,\,e)}(n,e) є відкритою частиною ключа, а(d,n) {\displaystyle (n,\,d)} — секретною. Числа {\displaystyle p\,} і {\displaystyle q\,} після генерації пари ключів можуть бути знищені, але в жодному разі не повинні бути розкриті. Формули шифрування і розшифрування використовують відкрити і закритий ключ відповідно а також велике число.Без секретного ключа майже неможливо розшифрувати повідомлення адже алгоритм використовує важкість розкладання на множники Для шифрування і дешифрування застосовують піднесення до ступеня по модулю. При використанні швидкого алгоритму піднесення до степеня по модулю здійснимо в поліноміальний час. Проте знаходження модульного логарифма так само складно, як і розкладання числа по модулю. Для нього немає алгоритму з поліноміальним часом |
