Теория графов. Задача о нефтепроводе максимальной пропускной способности. 20
 Скачать 0.63 Mb.
|
1.2 Сетевые графики. Порядок и правила построения.Сетевой моделью называется графическое изображение процессов, выполнение которых приводит к достижению одной или нескольких поставленных целей, с указанием установленных взаимосвязей между этими процессами. Сетевой график представляет собой сетевую модель с расчетными временными параметрами. Всякий намеченный комплекс работ, необходимых для достижения некоторой цели, называют проектом. Проект (или комплекс работ) подразделяется на отдельные работы. Каждая отдельная работа, входящая в комплекс (проект), требует затрат времени. Некоторые работы могут выполняться только в определенном порядке. При выполнении комплекса работ всегда можно выделить ряд событий, то есть итогов какой-то деятельности, позволяющих приступить к выполнению следующих работ. Если каждому событию поставить в соответствие вершину графа, а каждой работе — ориентированное ребро, то получится некоторый граф. Он будет отражать последовательность выполнения отдельных работ и наступление событий в едином комплексе. Если над ребрами проставить время, необходимое для завершения соответствующей работы, то получится сеть. Изображение такой сети называют сетевым графиком. Сетевой график состоит из двух типов основных элементов: работ и событий. Работа представляет собой выполнение некоторого мероприятия (например, погрузка боезапаса или переход корабля в пункт базирования). Этот элемент сетевого графика связан с затратой времен и расходом ресурсов. Поэтому работа всегда имеет начало и конец. На сетевом графике работа изображается стрелкой, над которой проставляется ее продолжительность или затрачиваемые ресурсы, или то и другое одновременно. Работа, отражающая только зависимость одного мероприятия от другого, называется фиктивной работой. Такая работа имеет нулевую продолжительность (или нулевой расход ресурсов) и обозначается пунктирной стрелкой. Начальная и конечная точки работы, то есть начало и окончание некоторого мероприятия, называются событиями. Следовательно, событие, в отличие от работы, не является процессом и не сопровождается никакими затратами времени или ресурсов. Событие, следующее непосредственно за данной работой, называется последующим событием по отношению к рассматриваемой работе. Событие, непосредственно предшествующее рассматриваемой работе, называется предшествующим. Наименования "предшествующий" и "последующий" относятся также и к работам. Каждая входящая в данное событие работа считается предшествующей каждой выходящей работе, и наоборот, каждая выходящая работа считается последующей для каждой входящей. Из определения отношения "предшествующий—последующий" вытекают свойства сетевого графика. Во-первых, ни одно событие не может произойти до тех пор, пока не будут закончены все входящие в него работы. Во-вторых, ни одна работа, выходящая из данного события, не может начаться до тех пор, пока не произойдет данное событие. И, наконец, ни одна последующая работа не может начаться раньше, чем будут закончены все предшествующие ей. Событие обозначается кружком с цифрой внутри, определяющей его номер. Из всех событий, входящих в планируемый процесс, можно выделить два специфических — событие начала процесса, получившее название исходного события, которому присваивается нулевой номер, и событие конца процесса ( завершающее событие), которому присваивается последний номер. Остальные события нумеруются так, чтобы номер предыдущего события был меньше номера последующего. Для нумерации событий применяется следующий способ. Вычеркиваются все работы, выходящие из события с номером "0", и просматриваются все события, в которых оканчиваются эти вычеркнутые работы. Среди просмотренных находятся события, которые не имеют входящих в них работ (за исключением уже вычеркнутых). Они называются событиями первого ранга и обозначаются (вообще, в произвольном порядке) числами натурального ряда, начиная с единицы (на рисунке 2 это событие 1). Затем вычеркиваются все работы, выходящие из событий первого ранга, и среди них находятся события, не имеющие входящих работ (кроме вычеркнутых). Это — события второго ранга, которые нумеруются следующими числами натурального ряда (например, 2 и 3 на рисунке 2). Проделав таким способом 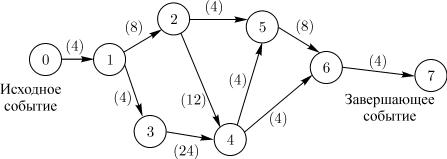 шаг, определяют события  -го ранга , и просматривая события, в которых эти работы заканчиваются, выбирают события, не имеющие ни одной входящей в них работы (кроме вычеркнутых). Это события k-го ранга, и нумеруются они последовательными числами натурального ряда, начиная с наименьшего, еще не использованного числа при предыдущей нумерации на -м шаге. Рисунок 2 – Пример сетевого графика Сетевой график содержит конечное число событий. Поскольку в процессе вычеркивания движение осуществляется в направлении стрелок (работ), никакое предшествующее событие не может получить номер, больший, чем любое последующее. Всегда найдется хотя бы одно событие соответствующего ранга, и все события получат номера за конечное число шагов. Работа обычно кодируется номерами событий, между которыми они заключены, то есть парой  , где i— номер предшествующего события, j— номер последующего события.В одно и то же событие могут входить (выходить) одна или несколько работ. Поэтому свершение события зависит от завершения самой длительной из всех входящих в него работ. Взаимосвязь между работами определяется тем, что начало последующей работы обусловлено окончанием предыдущей. Отсюда следует, что нет работ, не связанных началом и окончанием с другими работами через события. Последовательные работы и события формируют цепочки (пути), которые ведут от исходного события сетевого графика к завершающему. Например, путь 01234567 сетевого графика, показанного на рисунке 2, включает в себя события 0,1,2,3,4,5,6,7 и работы (0-1), (1-2), (2-5), (5-6), (6-7). На основании изложенного можно сказать, что ранг события — это максимальное число отдельных работ, входящих в какой-либо из путей, ведущих из нулевого (исходного) события в данное. Так, события первого ранга не имеют путей, состоящих более чем из одной работы, ведущих в них из 0 (например, событие 1 на рисунке 2). События второго ранга связаны с 0 путями, которые состоят не более чем из двух работ, причем для каждого события второго ранга хоть один такой путь обязательно существует. Например, на рисунке 2 событие 4 — событие третьего ранга, так как пути, ведущие в это событие из 0, включают только три работы — (0-1) (1-3)и (3-4) или (0-1),(1-2)и (2-4). Построенный таким образом сетевой график в терминах теории графов представляет собой направленный граф. На рисунке изображен сетевой график. Граф, не содержащий циклов и имеющий только один исток и только один сток, называется направленным графом. Сетевой график есть ориентированный связный асимметрический граф с одним истоком, одним стоком и без циклов, то есть это направленный граф. При этом вершинами графа служат события сетевого графика, а дугами (ребрами) — работы сетевого графика. Продолжительность работы представляет собой, в терминах теории графов, длину дуги. Следовательно, длина пути T— это сумма длин всех дуг, образующих данный путь, то есть  , где символом  обозначается дуга, которая соединяет вершины i и j и направлена от вершины i к вершине j.Обычно сетевой график строится от исходного события к завершающему, слева направо, то есть каждое последующее событие изображается несколько правее предыдущего. В планируемых процессах часто встречаются сложные комплексные связи, когда две или более работ выполняются параллельно, но имеют общее конечное событие, или когда для выполнения одной из работ необходимо предварительно выполнить несколько работ, а для другой, выходящей из общего для них события, предварительным условием является выполнение только одной из предшествующих работ и т.д. Изображение в сетевой модели подобных параллельных или дифференцированно зависимых работ выполняется следующим образом. В случае, когда наступление события (например, 3 на рисунке 3) возможно в результате завершения двух работ (1-3) и (2-4), но в то же время существует событие 4 (рисунок 3), зависящее от завершения только одной из этих работ (например, (2-4)), вводится фиктивная работа (4-3) (см. (рисунок 3). 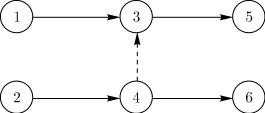 Рисунок 3 – Комплексные связи в сетевом графике Если одно событие (например, 1 на рисунке 4) служит началом двух (например, (1-2)и (1-3) или нескольких работ, заканчивающихся в другом событии (3 на рисунке 4)), то для их различия также вводится фиктивная работа (2-3). С помощью фиктивной работы в сетевом графике могут быть отражены и двусторонние связи (зависимости). 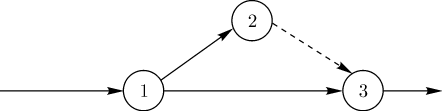 Рисунок 4 – Введение фиктивной работы Пусть, например, имеются три процесса A, B,C. При этом окончание процесса C зависит от результатов процессов A и B. В этом случае возникают двусторонние зависимости, которые можно изобразить так, как показано на рисунке 5. 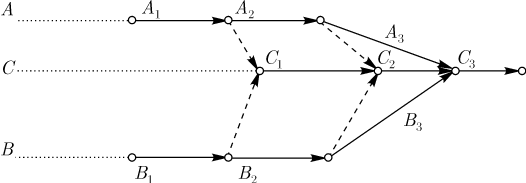 Рисунок 5 – Двусторонние зависимости Другое правило построения сетевого графика заключается в том, что если несколько работ может начаться не после полного, а после частичного выполнения определенной работы, то последнюю работу целесообразно представить как сумму ее частей, расчлененных событиями ( 1, 2, 3, 4и 5на рисунке 6). 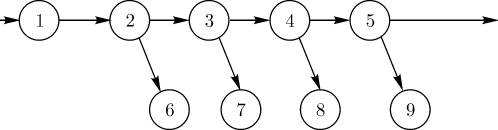 Рисунок 6 – Вариант представления последней работы Для отображения времени и места поступления дополнительных ресурсов (например, пополнение личного состава, топлива и т.д.) и другой информации на сетевом графике закрашенным кружком изображаются так называемые подставки (рисунок 7). При наличии двух и более работ, выходящих из события, с которым необходимо связать подставку, последняя соединяется с дополнительно введенным событием через фиктивную работу (рисунок 7). После построения сетевого графика проверяется отсутствие работ, имеющих одинаковые коды. При наличии таких работ вводятся дополнительные события и фиктивные работы. Кроме того, сетевой график должен содержать только одно исходное событие и только одно завершающее событие. 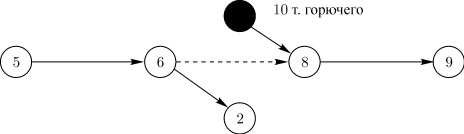 Рисунок 7 – Подставки в сетевом графике Если эти условия не выполнены, то необходимо добавить еще одно исходное событие и соединить его стрелками с имеющимися несколькими начальными событиями или добавить еще одно конечное событие, к которому ведут стрелки от нескольких имеющихся конечных событий. Сетевой график не должен иметь циклов, то есть таких путей, в которых конец последней работы совпадает с началом первой работы. Сетевой график, имеющий хотя бы один цикл, не может быть реализован, так как ни одна из работ, входящих в такой цикл, никогда не может начаться. Анализ сетевой модели Параметры сетевой модели. Параметрами сетевой модели являются: наиболее ранее возможное время наступления j-го события, обозначаемое символом  ;самое позднее допустимое время наступления i-го события, обозначаемое символом  ;резерв времени данного события, обозначаемый символом  ;полный резерв времени работы (i,j), обозначаемый символом  ;свободный резерв времени работы (i,j), обозначаемый символом  .Наиболее раннее возможное время наступления j-го события определяется следующий рекуррентной формулой: 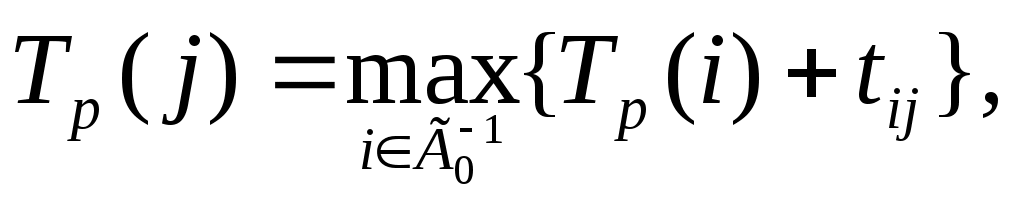 где  — продолжительность (i,j)-й работы; — множество событий, предшествующих j-му событию.Вычисления по формуле выполняются шаг за шагом, двигаясь в порядке нумерации событий. Резервом времени данного события называется разность между  и  , которая вычисляется по формуле .Полный резерв времени работы (i, j) вычисляется по формуле  Свободный резерв времени работы (i, j) вычисляется по формуле  |