|
|
Основные формулы теория вероятностей. Основные формулы теория вероятностей Операции над событиями
Глава 3. Основные формулы теория вероятностей
§ 1. Операции над событиями.
Суммой двух событий А и В называется событие АВ (А+В), заключающееся в том, что произойдет хотя бы одно из событий А или В (либо событие А, либо событие В либо А и В одновременно).
Произведением (или пересечением)двух событий А и В называется событие АВ (АВ), состоящее в одновременном появлении и события А и события В.
Вероятность суммы двух событий вычисляется по формуле (теорема сложения)
 . .
События А1,А2,...,Ак образуют полную группу событий, если в результате испытания непременно произойдет одно из них , т.е. 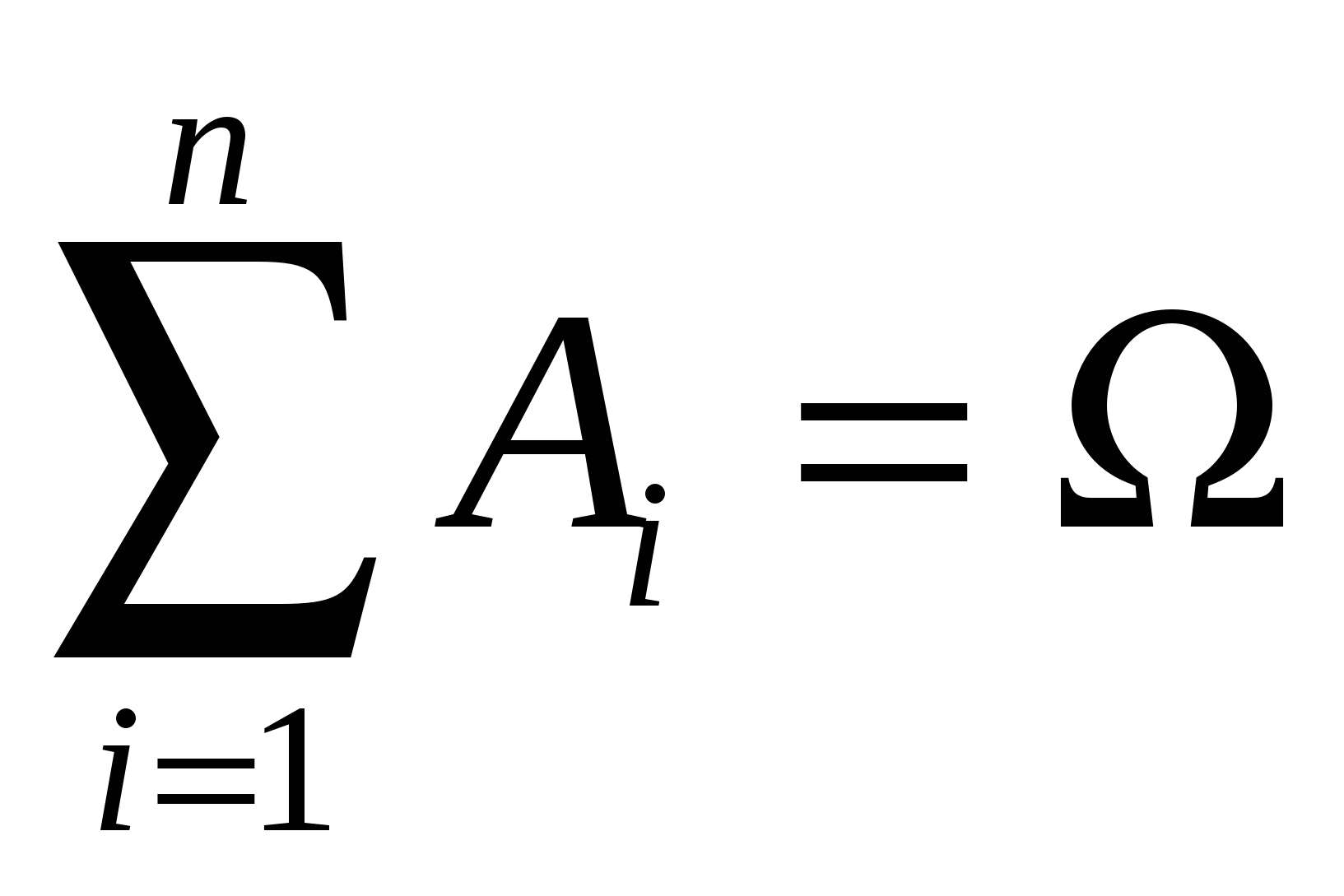 . .
События А и В называются несовместными (непересекающимися), если они не могут произойти одновременно АВ=. Если события несовместны, то
Р(АВ) = 0 и Р(А + В) = Р(А) + Р(В).
Задача 1. В ящике 10 красных и 5 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность, что пуговицы будут одноцветными?
Решение. Событие A={вынуты пуговицы одного цвета} можно представить в виде суммы  , где события , где события  и и  означают выборку пуговиц красного и синего цвета соответственно. Вероятность вытащить две красные пуговицы равна означают выборку пуговиц красного и синего цвета соответственно. Вероятность вытащить две красные пуговицы равна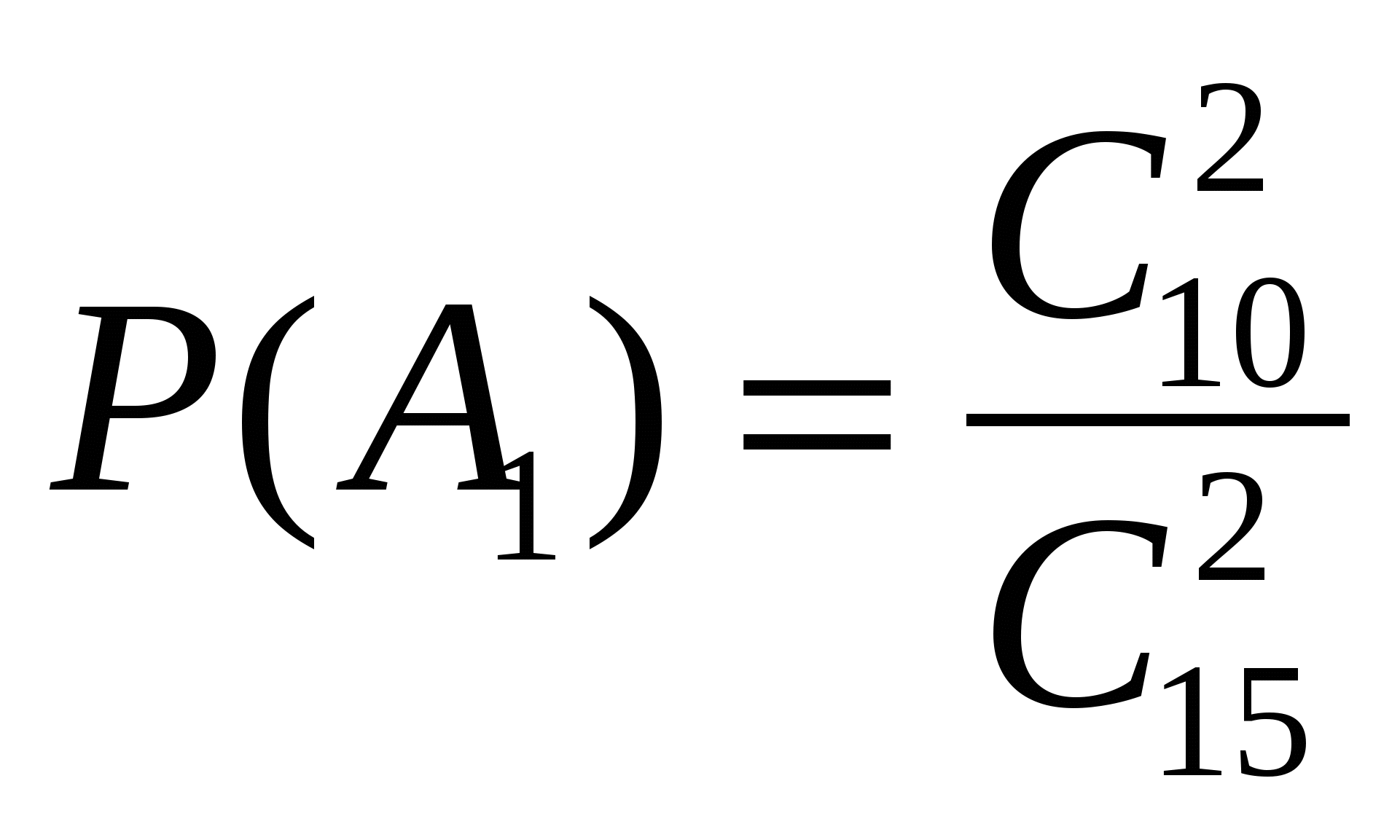 , а вероятность вытащить две синие пуговицы , а вероятность вытащить две синие пуговицы  . Так как события . Так как события  и и  не могут произойти одновременно, то в силу теоремы сложения не могут произойти одновременно, то в силу теоремы сложения

§ 2. Условная вероятность и теорема умножения.
Помимо обычной (безусловной) вероятности можно рассматривать так называемую условную вероятность, вычисляемую при условии, что событие B произошло. Такую вероятность (вероятность А при условии В) обозначают Р(А|В) и вычисляют с помощью одной из двух формул:
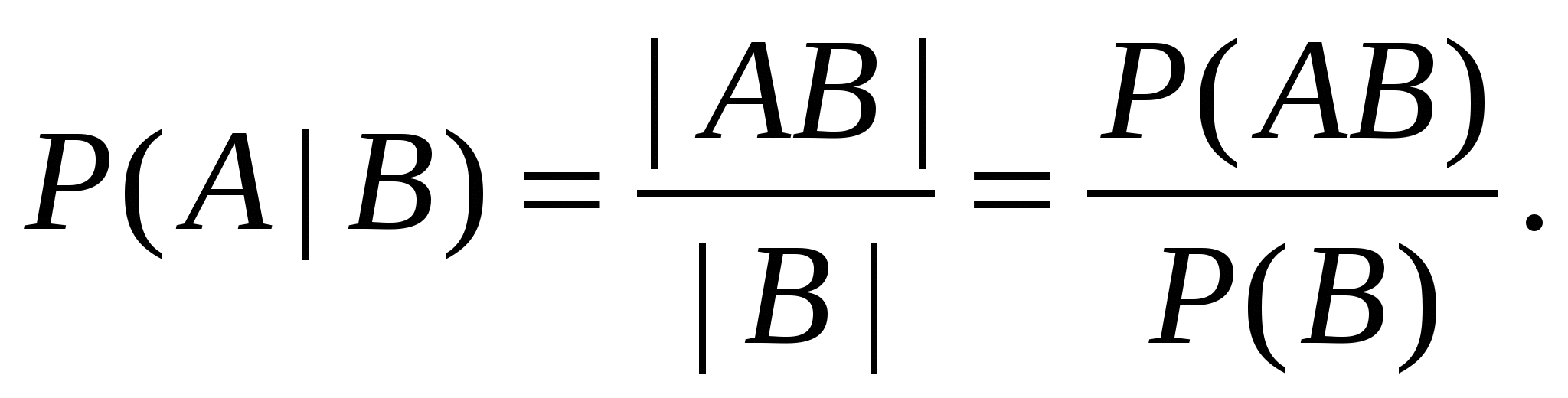
Из этой формулы вытекает формула для вероятности произведения двух событий (теорема умножения)
 . .
Формула умножения для трех событий:
 . .
Задача 2. В семье – двое детей. Какова вероятность, что старший ребенок – мальчик, если известно, что в семье есть дети обоего пола?
Решение. Пусть А={старший ребенок – мальчик}, B={в семье есть дети обоего пола}. Будем считать, что рождения мальчика и рождение девочки – равновероятные события. Если рождение мальчика обозначить буквой М, а рождение девочки – Д, то пространство всех элементарных исходов состоит из четырех пар:  . В этом пространстве лишь два исхода (МД и ДМ) отвечают событию B. Событие AB означает, что в семье есть дети обоего пола и старший ребенок – мальчик, это значит, что второй (младший) ребенок – девочка. Этому событию AB отвечает один исход – МД. Таким образом, |AB|=1, |B|=2 и . В этом пространстве лишь два исхода (МД и ДМ) отвечают событию B. Событие AB означает, что в семье есть дети обоего пола и старший ребенок – мальчик, это значит, что второй (младший) ребенок – девочка. Этому событию AB отвечает один исход – МД. Таким образом, |AB|=1, |B|=2 и

Задача 3. Мастер, имея 10 деталей, из которых 3 – нестандартных, берет и проверяет детали одну за другой, пока нему не попадется стандартная. Какова вероятность, что он проверит ровно две детали.
Решение. Событие А={мастер проверил ровно две детали} означает, что при такой проверке первая деталь оказалась нестандартной, а вторая – стандартная. Значит,  , где , где  ={ первая деталь оказалась нестандартной } и ={ первая деталь оказалась нестандартной } и  ={вторая деталь – стандартная}. Очевидно, что вероятность ={вторая деталь – стандартная}. Очевидно, что вероятность  кроме того, кроме того,  (так как перед взятием второй детали у мастера осталось 9 деталей, из которых только 2 нестандартные и 7 стандартных). По теореме умножения (так как перед взятием второй детали у мастера осталось 9 деталей, из которых только 2 нестандартные и 7 стандартных). По теореме умножения
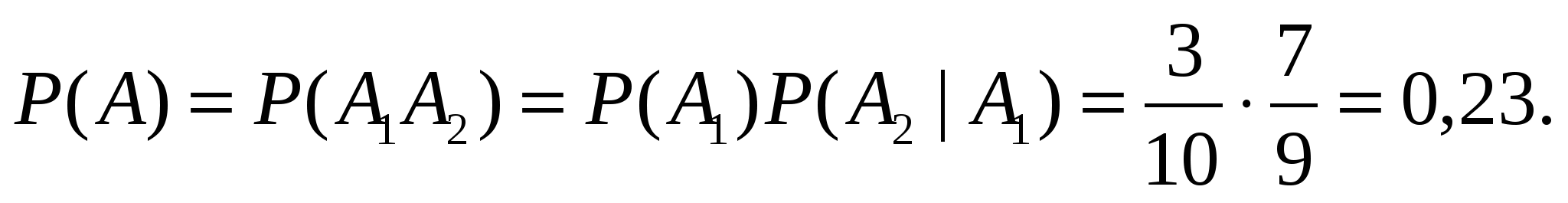
§ 3. Независимость событий.
Событие А не зависит от В, если появление события В не меняет значения вероятности события А, т.е. условная вероятность равна безусловной: Р(А/В) = Р(А). Аналогично определяется независимость события B от A. Оказывается, что свойство независимости на самом деле симметрично относительно событий A и B, и потому определение независимости двух событий принимает более простой вид:
два события A и B независимы, если справедливо равенство
Р(АВ) = Р(А) Р(В).
Это равенство можно использовать также как удобный критерий независимости при практической проверке независимости двух событий.
Задача 4. В одном ящике 3 белых и 5 черных шаров, в другом ящике – 6 белых и 4 черных шара. Найти вероятность того, что хотя бы из одного ящика будет вынут один белый шар, если из каждого ящика вынуто по одному шару.
Решение. Событие A={хотя бы из одного ящика вынут белый шар} можно представить в виде суммы  , где события , где события  и и  означают выборку одного белого шара из первого и второго ящика соответственно. Вероятность вытащить белый шар из первого ящика равна означают выборку одного белого шара из первого и второго ящика соответственно. Вероятность вытащить белый шар из первого ящика равна , а вероятность вытащить белый шар из второго ящика , а вероятность вытащить белый шар из второго ящика  . Кроме того, в силу независимости . Кроме того, в силу независимости  и и  имеем: имеем: 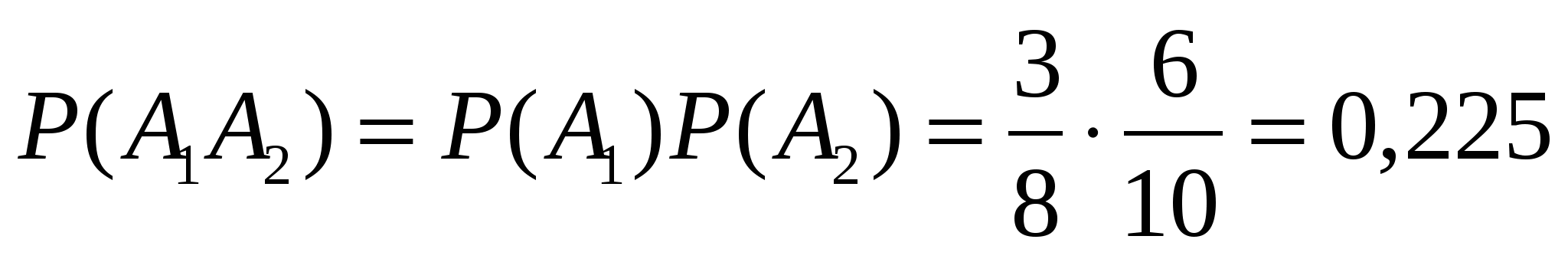 . По теореме сложения получаем: . По теореме сложения получаем:
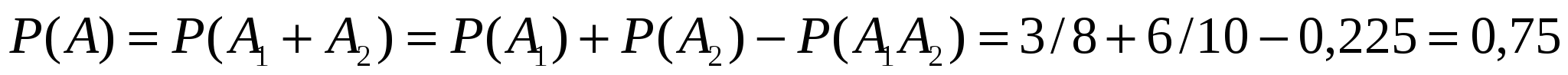 . .
§ 4. Формула полной вероятности.
Пусть событие А может быть реализовано только при условии появления одного из событий Hi, i = 1,..., n. Предположим, что события Hi несовместны, образуют полную группу (т.е. в результате испытания непременно произойдет одно из них) и вероятности их до опыта известны.. Такие события Hi называются гипотезами. Тогда вероятность события А можно вычислить с помощью формулы полной вероятности:
 . .
Задача 5. Три экзаменатора принимают экзамен по некоторому предмету у группы в 30 человек, причем первый опрашивает 6 студентов, второй — 3 студента, а третий — 21 студентов (выбор студентов производится случайным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у первого преподавателя равны 40%, у второго — только 10%, зато у третьего — 70%. Найти вероятность того, что слабо подготовившийся студент сдаст экзамен.
Решение. Обозначим через  – гипотезы, состоящие в том, что слабо подготовившийся студент отвечал первому, второму и третьему экзаменатору соответственно. По условию задачи – гипотезы, состоящие в том, что слабо подготовившийся студент отвечал первому, второму и третьему экзаменатору соответственно. По условию задачи
 , ,  , ,  . .
Пусть событие A={слабо подготовившийся студент сдал экзамен}. Тогда снова в силу условия задачи
 , ,  , ,  . .
По формуле полной вероятности получаем:
 . .
Для решения задач такое типа удобно использовать так называемое "дерево" вероятностей. Из формулы полной вероятности следует, что для вычисления вероятности события А необходимо осуществить перебор всех путей, ведущих к результирующему событию А; вычислить и расставить на соответствующих путях вероятности Р(Нi) того, что движение будет происходить по данному пути, и вероятности Р(А/ Нi) того, что на данном пути будет достигнуто конечное событие А. Затем вероятности, стоящие на одном пути, перемножаются, а результаты, полученные для различных путей, складываются.
Каждое из условий может в свою очередь делиться на несколько дополнительных условий или гипотез, т.е. на каждом этапе оно допускает неограниченное число ветвлений схемы, поэтому в решении задач удобнее пользоваться не самой формулой полной вероятности, а графической схемой полной вероятности, которую называют "деревом" вероятностей.
§ 5. Формулы Байеса.
Предположим теперь другую ситуацию: пусть теперь известно, что событие A произошло. Это знание влияет на нашу оценку вероятностей гипотез Нk, т.е. на вероятность того, что событие A произошло именно путем Нk. Эти условные вероятности (т.е. при условии, что событие А произошло), вычисляются с помощью формулы Байеса:
 . .
Отметим, что в знаменателе этой формулы записана ничто иное как вероятность Р(А), вычисленная по формуле полной вероятности.
Задача 6. (см. задачу 4) Известно, что студент сдавал экзамен, но получил «неуд». Кому из трех преподавателей вероятнее всего он отвечал?
Решение. Вероятность получить «неуд» равна  . Требуется вычислить условные вероятности . Требуется вычислить условные вероятности 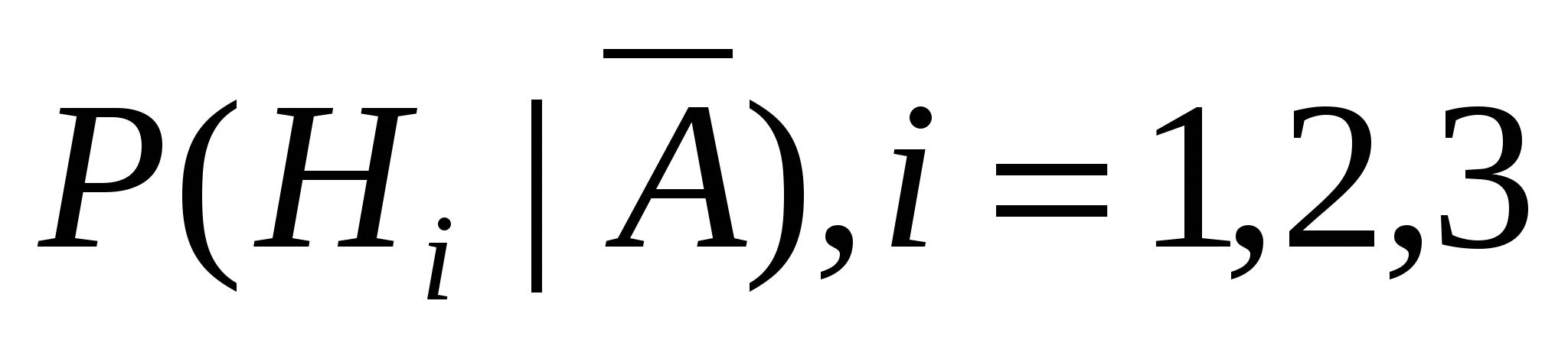 . По формулам Байеса получаем: . По формулам Байеса получаем:
 , ,
и аналогично,
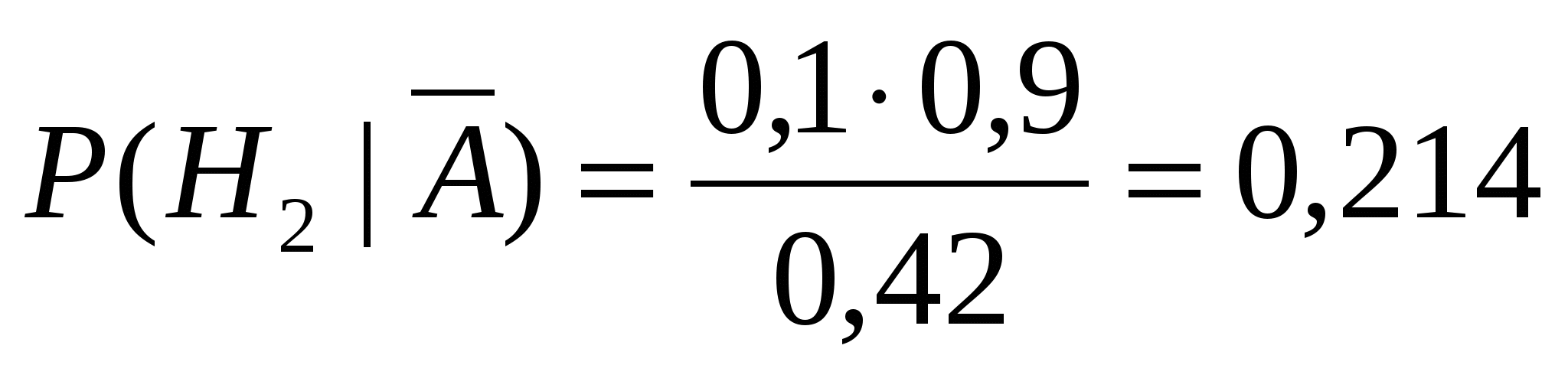 , , 
Отсюда следует, что вероятнее всего слабо подготовившийся студент сдавал экзамен третьему экзаменатору.
Задачи для самостоятельного решения
Рабочий обслуживает три независимо работающих станка. Событие Аi ={ i-ый станок в течении часа потребует наладки}, Р(Аi)=0,2, i=1,2,3. Выразить события: а) ровно два станка потребуют наладки; б) не более двух потребуют наладки; в) хотя бы один потребует наладки. Найти вероятность события в).
Стрелок делает три выстрела, при этом он поражает цель с вероятностью 0,6 при одном выстреле. Событие Аi={ i-ая пуля попала в цель }, i=1,2,3. Выразить события: а) было хотя бы одно попадание; б) ровно одно попадание; в) не менее двух попаданий. Найти вероятность события в).
В коробке 4 детали. Мастер извлекает детали до тех пор, пока не вытащит годную. Событие  = { i-ая извлеченная деталь является годной }, = { i-ая извлеченная деталь является годной }, 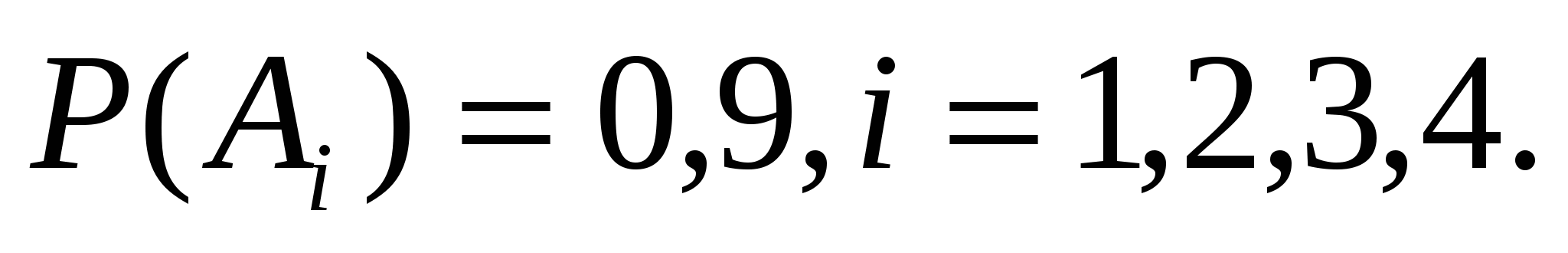 Выразить события, состоящие в том, что мастер сделал а) ровно одно извлечение; б) ровно 2 извлечения; в) не менее двух извлечений. Найти вероятность б). Выразить события, состоящие в том, что мастер сделал а) ровно одно извлечение; б) ровно 2 извлечения; в) не менее двух извлечений. Найти вероятность б).
Пусть А,В,С – три произвольных события. Найти выражение для событий, состоящих в том, что: а) произошли все три события; б) произошло хотя бы одно из событий; в) произошли хотя бы два события; г) произошли два и только два события; д) произошло ровно одно событие; е) ни одно событие не произошло; ж) произошло не более двух событий.
Прибор состоит из трех блоков первого типа и четырех блоков второго типа. Событие Аi ={исправен i-ый блок первого типа}, i=1,2,3, Вj = {исправен j-ый блок второго типа}, j=1,2,3,4. Прибор работает, если исправны хотя бы один блок первого типа и не менее трех блоков второго типа. Найти выражение для события С, которое соответствует работающему состоянию прибора.
В пакете с леденцами лежит 4 красных, 5 желтых и 6 зеленых конфет. Найти вероятность наудачу вынуть подряд 3 конфеты одного цвета.
В партии из 20 изделий 4 бракованных. Найти вероятность того, что в выборке из 5 изделий не более одного бракованного.
В лифт 9-этажного дома на первом этаже входят 6 человек. Для каждого человека равновероятен выход на любом из 8 этажей. Известно, что все вышли на разных этажах. При этом условии найти вероятность, что на первых трех этажах вышли два человека.
Три пассажира садятся в поезд, случайно выбирая любой из 6 вагонов. Какова вероятность, что хотя бы один из них сядет в первый вагон, если известно, что они сели в разные вагоны?
В ящике 12 красных , 8 зеленых и 10 синих шаров .Наудачу вынимаются два шара. Какова вероятность, что вынутые шары разного цвета, если известно, что не вынут синий шар?
Шесть шаров случайным образом раскладывают в три ящика. Найти вероятность, что во всех ящиках разное число шаров при условии, что все они не пустые.
Двое шахматистов равной силы играют 4 партии. Найти вероятность, что победил первый, если известно, что каждый выиграл хоть один раз.
В лифт на цокольном этаже входят 5 человек. Считая для каждого человека равновероятном выход на любом из 9 этажей, найти вероятность того, что двое из них выйдут на одном этаже, а остальные на разных.
Известно, что 5-значный номер телефона имеет все цифры разные. Какова вероятность при этом условии, что среди них ровно четная (0 считаем четной цифрой и телефонный номер может начинаться с нуля).
Пять человек случайным образом (независимо друг от друга) выбирают любой из 7 вагонов поезда. Известно, что некоторые 2 вагона остались пустыми. Какова вероятность при этом условии, что все сели в различные вагоны, в том числе в первый и во второй?
В урне 5 белых и 10 черных шаров. Извлечены 6 шаров (с возвращением). Известно, что среди них есть белые шары. При этом условии найти вероятность того, что среди них будут также не менее двух черных шаров.
Семь пассажиров случайным образом выбирают один из 9 вагонов поезда. Известно, что они сели в разные вагоны, при этом условии найти вероятность того, что в первых трех вагонах поезда будут ехать два человека.
Распределяются 5 шаров по трем ящикам. Известно, что нет пустых ящиков. При этом условии найти вероятность, что в первом ящике лежит один шар.
В четырех группах учится 100 человек (по 25 человек в каждой). На олимпиаду отобрано 5 человек. Какова вероятность, что среди них будут представители всех классов?
Сколько раз надо бросить игральную кость, чтобы на 95% быть уверенным в том, что хотя бы при одном бросании появится «шестерка»?
Известно, что в пятизначном номере телефона все цифры разные. Найти вероятность того, что среди них есть цифры 1 и 2.
Бросают три кубика. Какова вероятность того, что хотя бы на одном из них выпадет «шестерка», если известно, что на всех кубиках выпали разные грани?
Фирма участвует в 4 проектах, каждый из которых может закончиться неудачей с веростностью 0,1. В случае неудачи одного проекта вероятность разорения фирмы равна 20%, двух – 50%, трех – 70%, четырех – 90%. Найти вероятность разорения фирмы.
Два аудитора проверяют 10 фирм (по 5 фирм каждый), у двух из которых имеются нарушения. Вероятность обнаружения нарушений первым аудитором равна 80%, вторым – 90%. Найти вероятность, что обе фирмы-нарушители будут выявлены.
В первой урне лежат один белый и три черных шара, а во второй урне – 2 белых и 1 черный шар. Из первой урны во вторую перекладывается не глядя один шар, а затем один шар перекладывается из второй урны в первую. После этого из первой урны вынули один шар. Найти вероятность, что он белый.
В прибор входит комплект из двух независимых деталей, вероятность для которых выйти из строя в течение года соответственно равна 0,1 и 0,2. Если детали исправны, то прибор работает в течение года с вероятностью 0,99. Если выходит из строя только первая деталь, то прибор работает с вероятностью 0,7, а если только вторая – то с вероятностью 0,8. Если выходят из строя обе детали, прибор будет работать с вероятностью 0,1. Какова вероятность, что прибор будет работать в течение года?
Электроэнергия поступает в город через три электролинии, каждая из которых может быть отключена с вероятностью 0,1. Если отключена одна электролиния, город испытывает недостаток электроэнергии с вероятностью 0,8. Если отключены три электролинии, недостаток электроэнергии ощущается с вероятностью 0,5. Если же отключены все три электролинии, то недостаток электроэнергии есть с вероятностью 1. В случае, когда работают все электролинии, недостатка энергии нет. Какова вероятность, что в день проверки город испытывает недостаток электроэнергии?
Фирма нарушает закон с вероятностью 0,25. Аудитор обнаруживает нарушения с вероятностью 0,75. Проведенная им проверка не выявила нарушений. Найти вероятность, что они на самом деле есть.
Изделие имеет скрытые дефекты с вероятностью 0,2. В течение года выходит из строя 75% изделий со скрытыми дефектами и 15% изделий без дефектов. Найти вероятность, что изделие имело скрытые дефекты, если оно вышло из строя в течение года.
Из урны, где было 4 белых и 6 черных шаров, потерян один шар неизвестного цвета. После этого из урны извлечены (без возвращения) два шара, оказавшиеся белыми. При этом условии найти вероятность, что потерян был черный шар.
Производственный брак составляет 4%. Каждое изделие равновероятным образом поступает к одному из двух контролеров, первый из которых обнаруживает брак с вероятностью 0,92, второй – 0,98. Какова вероятность, что признанное годным изделие является бракованным.
В центральную бухгалтерию корпорации поступили пачки накладных для проверки и обработки. 90% пачек были признаны удовлетворительными: они содержали 1% неправильно оформленных накладных. Остальные 10% накладных были признаны неудовлетворительными, т.к. они содержали 5% неправильно оформленных накладных. Какова вероятность того, что взятая наугад накладная оказалась неправильно оформленной? (р1=0,1; р2=0,014)
Известно, что проверяемая фирма может уйти от налогов с вероятностью 40% и выбрать для этого одну из трех схем (равновероятно). Найти вероятность, что фирма уходит от налогов по третьей схеме, если по первым двум схемам нарушений не обнаружено.
Стрелок А поражает мишень с вероятностью 0,6., стрелок Б - с вероятностью 0,5 и стрелок В – с вероятностью 0,4. Стрелки дали залп по мишени, и две пули попали в цель. Что вероятнее: попал стрелок В в мишень или нет?
Имеются три партии по 20 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 20, 15 и 10. Из наудачу выбранной партии извлечена деталь, оказавшейся стандартной. Деталь возвращают в партию и вторично из той же партии наугад извлекают деталь, которая оказывается стандартной. Найти вероятность того, что детали были извлечены из третьей партии.
|
|
|
 Скачать 142 Kb.
Скачать 142 Kb.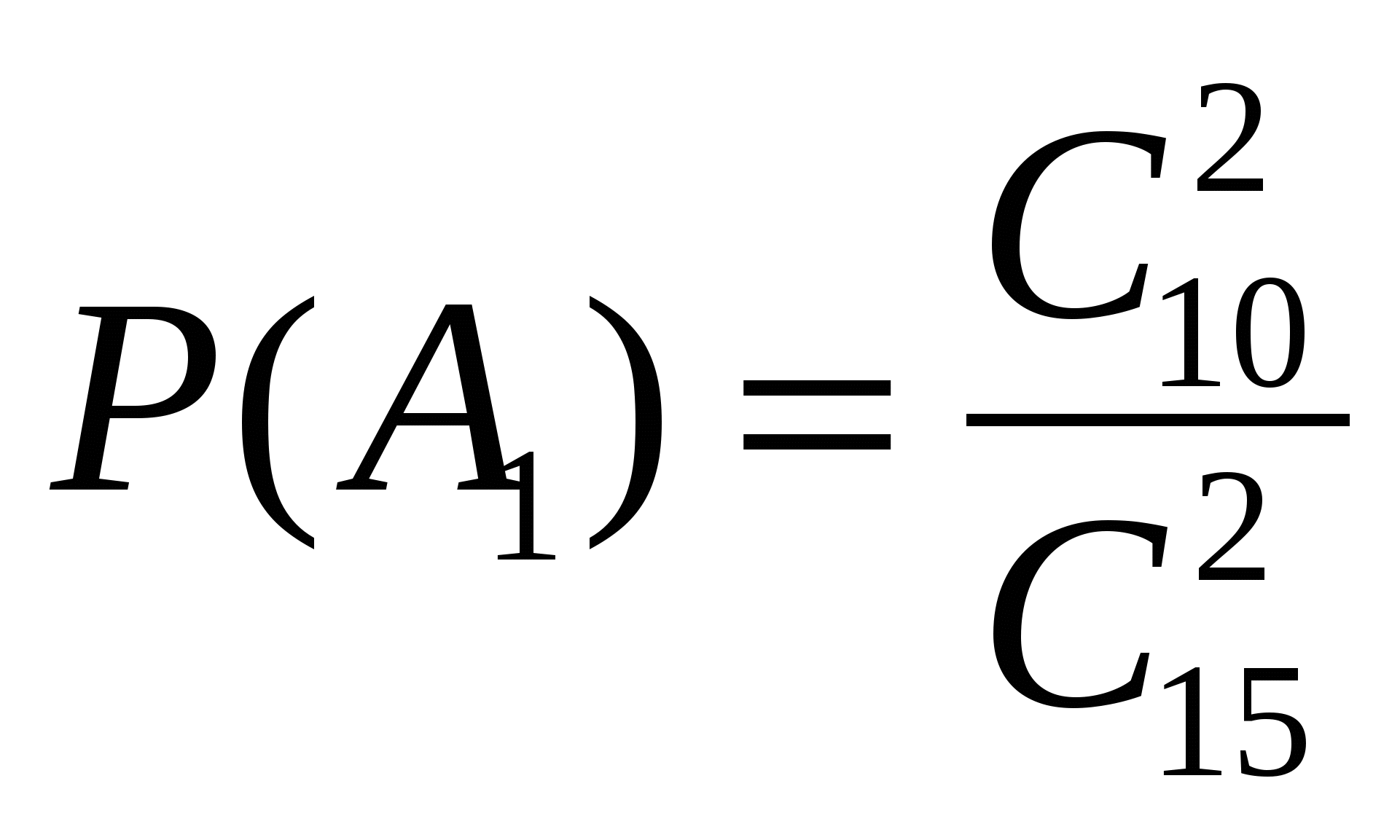 , а вероятность вытащить две синие пуговицы
, а вероятность вытащить две синие пуговицы  . Так как события
. Так как события 
 .
.