Д1 моя_ргр. Задача Определить давление в верхнем цилиндре гидропреобразователя (мультипликатора), если показание

Название	Задача Определить давление в верхнем цилиндре гидропреобразователя (мультипликатора), если показание
Дата	06.12.2022
Размер	0.79 Mb.
Формат файла
Имя файла	Д1 моя_ргр.doc
Тип	Задача #831827

Министерство образования и науки

Российской Федерации

Федеральное государственное

Бюджетное образовательное учреждение

Высшего профессионального образования

Вятский Государственный Университет

Кафедра теплотехники и гидравлики

Расчётно-графическая работа

по дисциплине “Гидравлика”

Вариант Д1

Выполнил: студент группы ТМ -31 Клименко К. Д.

Проверил: Акчурин Р.Ю.

Киров 2012

Задача 4.

Определить давление

в верхнем

цилиндре гидропреобразователя

(мультипликатора), если показание

манометра, присоединенного

к нижнему цилиндру, равно

.

Поршни перемещаются вверх,

причем сила трения составляет 10%

от силы давления жидкости на нижний

поршень. Вес поршней G. Диаметры

поршней: D, d. Высота Н. Плотность

масла

кг/м³.
Дано:

;

кг/м³

Найти:

- ?
Решение:
Принимается:

р₁ – давление, действующее на нижний поршень диаметром D;

р₂– давление, действующее на верхний поршень диаметром d.
Сила давления на нижний поршень определяется по формуле:

,

где р₁ – абсолютное (полное) давление;

– площадь поверхности нижнего поршня.

Следовательно:

Силы, действующие в данной системе: Р_тр, G, Р₁и Р₂.

Спроецируем их на ось у, которая направлена вверх:

(по условию)

Из этой формулы выражается сила давления на верхний поршень:

(1)
Сила давления

также определяется по следующей формуле:

. (2)
Приравниваются правые части выражений (1) и (2):

,

Находится давление в верхнем цилиндре р₂:

,

где

– сила давления на нижний поршень,

;

G – вес поршня, G= 4100 Н;

– площадь поверхности верхнего поршня:

,
Следовательно,

Ответ:

.

Задача 5.
Давление в цилиндре гидравлического пресса повышается в результате нагнетания в него жидкости ручным поршневым насосом и сжатия ее в цилиндре. Определить число двойных ходов n поршня ручного насоса, необходимое для увеличения силы прессования детали А от 0 до 0,8 МН, если диаметры поршней: D и d; ход поршня ручного насоса l; объемный модуль упругости жидкости Е =1300 МПа; объем жидкости в цилиндре пресса V.

Чему равно максимальное усилие Р на рукоятке насоса при ходе нагнетания, если b/a известно.

Построить эпюру давления масла по высоте l, а также эпюру полного давления.
Дано:

;

.

Найти:

Решение:
Составляется сумма

моментов относительно т.О:

, (1)

где Р – усилие на рукоятке насоса.
Силу Р₁ уравновешивает противодействующая ей сила R.
Из уравнения (1) определяется сила R:

Сила давления, действующая на поршень насоса, соответственно, равна:

, (2)

Давление под поршнем насоса определяется по формуле:

,

где Р₁ – сила давления, действующая на поршень насоса;

– площадь поверхности поршня диаметром d:

.
Следовательно, давление под поршнем насоса равно: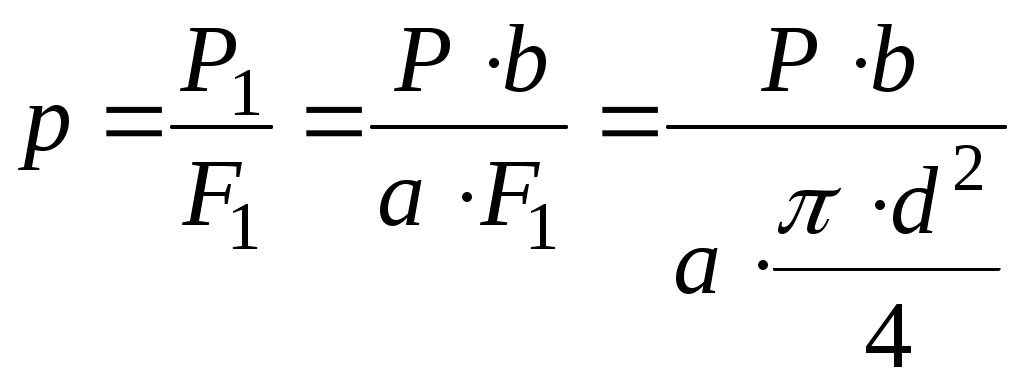

(3)

Так как усилие Р на рукоятке насоса будет максимальным при

(так как необходимо преодолевать сопротивление масла в прессе), получается:

, (4)

где р – полное давление под поршнем насоса:

– площадь поверхности поршня диаметром D:

(5)
Тогда, подставив в формулу (4) выражения (3) и (5), получается зависимость для определения силы давления Р₂:

Отсюда выражается Р_max:

,

где

(по условию)
Окончательно получается величина максимального усилия Р на рукоятке насоса:

Число двойных ходов n поршня ручного насоса определяется по формуле:

, (6)

где V – объем, который необходимо закачать в пресс для увеличения усилия до 0,8 МН;

V_п.н – объем поршневого насоса.
Жидкость имеет свойство сжимаемости, то есть способность изменять свой объем при изменении давления. Сжимаемость характеризуется коэффициентом объемного сжатия

, который представляет собой относительное изменение объема, приходящееся на единицу давления, то есть:

, (7)

где dV– абсолютное изменение объема;

V_н – начальный объем жидкости в прессе,

;

dp –абсолютно изменение давления;

Е – объемный модуль упругости жидкости, Е =1300 МПа.
Знак минус в формуле обусловлен тем, что положительному приращению давления р соответствует отрицательное приращение (т.е. уменьшение) объема V.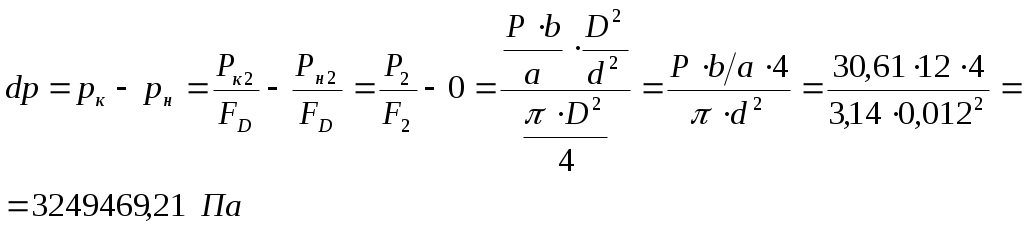

Из формулы (7) находится абсолютное изменение объема dV:

,
Число двойных ходов n поршня ручного насоса определяется по формуле (6):

,
Строятся эпюры давления масла по высоте l и полного давления.
Давление столба жидкости (масла) высотой l:

,

где

– плотность масла,

;

l – высота столба жидкости, l= 0,032 м.

При l = 0:

;

При l = 0,032 м:

Эпюра давления масла имеет вид:

Для построения эпюры полного давления необходимо найти величиину полного давления:

,

где р – внешнее давление (в данной задаче – давление под поршнем насоса):

;

– давление столба жидкости высотой l,

.
Определяется давление под поршнем насоса:

,

где

– по формуле (2), принимается Р = P_max.

.
Следовательно,

.

Приl = 0:

при l = 0,026 м:

Эпюра полного давления имеет вид:

Ответ:

.

Задача 12.
На какую высоту h может засасываться вода водоструйным насосом, если по нему протекает вода с расходом Q? Диаметры d₁ и d₂, избыточное давление в первом сечении р_1изб. Потери напора по причине их незначительности можно не учитывать.

Дано:

;

;

g = 9,81 м/c².
Найти:

h - ?

Решение:
Уравнение Бернулли для сечений 1 - 1 и 2 – 2 относительно плоскости сравнения 0 – 0

(1)

, где:

Р₁ – полное давление.
Давление на уровне А – А

, где:

р₂ – абсолютное давление.
Объёмный расход жидкости

,

отсюда

Тогда из уравнения (1):

отсюда

Ответ:

.

Задача 16.

Из бака А, в котором поддерживается постоянный уровень, вода перетекает по цилиндрическому насадку диаметром d₁ в бак В, из которого сливается в среду с атмосферным давлением по короткой трубке диаметром d₂. Напор Н, ось насадка размещена на глубине h под уровнем воды в баке А.

Найти зависимость расхода воды, перетекающей из бака А в бак В, от коэффициента сопротивления

крана, установленного на трубке.

Определить наименьшее значение

, начиная с которого дальнейшее

увеличение открытия крана (то есть уменьшение

) не будет приводить к увеличению расхода воды.

Потери напора на трение по длине короткой трубки не учитывать.

Указания. Используя уравнение Бернулли для сечений 0-0 и 1-1 потока жидкости, получить формулу расхода воды через короткую трубку диаметром d₂. Расход через цилиндрический насадок диаметром d₁ равен расходу через короткую трубку диаметром d₂. Наименьшее значение

определится из условия

Дано:

;

;

Найти:

Q(

) -?

- ?
Решение:

Уравнение Бернулли для сечений

0-0, 1-1, относительно плоскости

сравнения, проходящей через центр насадка:

,

где: v₀ – средняя скорость на поверхности в резервуаре В, v₀=0;

v₁ – средняя скорость на выходе из крана;

- коэффициенты неравномерности распределения скоростей в сечениях 0-0 и 1-1 соответственно;

– местные потери,

- коэффициент сопротивления на входе в трубку,

.

Тогда:

Расход через трубку определится: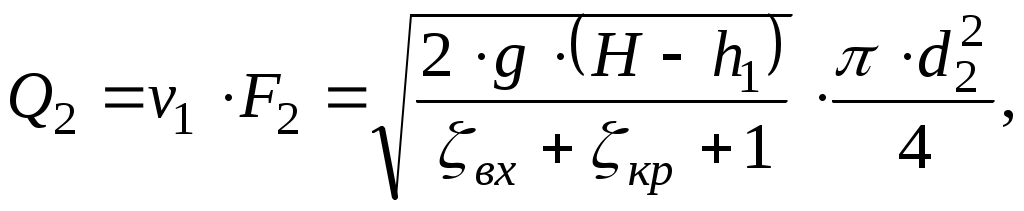

где: F₂ – площадь сечения трубки.
Расход через цилиндрический насадок определяется по формуле:

где: μ – коэффициент расхода. Для цилиндрического насадка μ=0,81;

F₁ – площадь сечения насадка,

.

Расход через цилиндрический насадок диаметром d₁ равен расходу через короткую трубку диаметром d₂, то есть: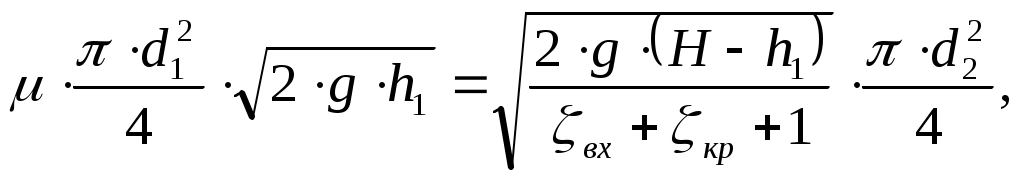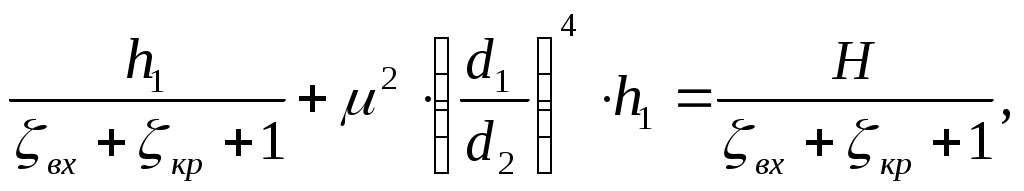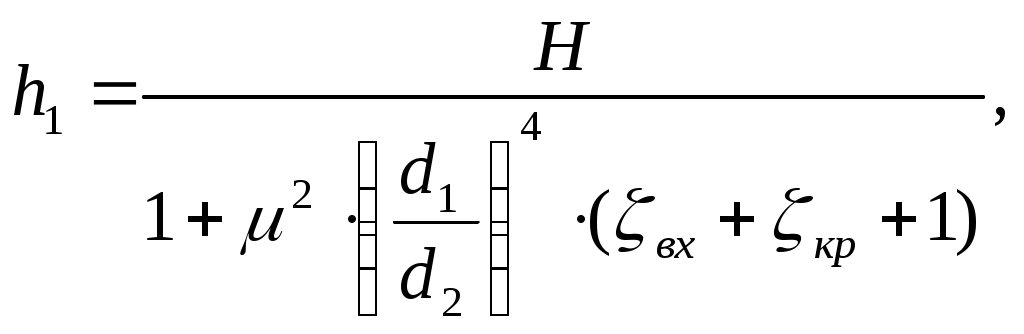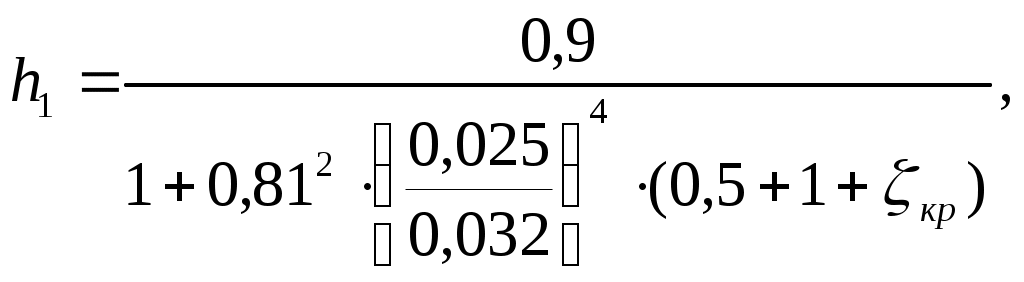

Расход воды перетекающей из бака А в бак В: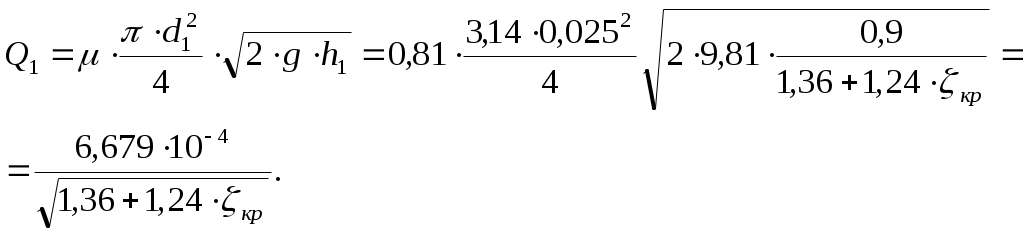

Значение

определяем из условия: h₁= h+d₁/2

Ответ:

Задача 20.
Определить расход жидкости Ж, протекающей по трубопроводу в пункты 1 и 2, если напор Н в резервуаре постоянный. Длины отдельных частей трубопровода равны l, l₁, l₂, а диаметры - d, d₁, d₂. Температура жидкости 20 ⁰С. Местные потери напора в расчетах не учитывать. Числовые данные, необходимые для решения задачи, выбрать из таблицы.

Указания:

Задача решается графоаналитическим способом, при этом даются различные значения Q и определяется Н. По значениям Н и Q строятся графики зависимости . Затем строится суммарная характеристика трубопровода при параллельном их соединении и по известному значению Н определяется Q.
Пример построения пьезометрической и напорной линии приводится в приложении А.

Дано:
Материал: сталь нержавеющая; Жидкость Ж: бензин авиационный; Н = 7,20 м ; l = l₁ = 9,20 м; l₂ = 11,00 м; d = 50 мм; d₁ = d₂ = 40 мм; ; Δ_э=0,075 мм. Найти:
Q₁ -? Q₂ -?

Решение:

При расчете трубопровода пренебрегают местными сопротивлениями.

Можно считать, что расход через трубы 1 и 2 равен половине расхода в трубе 0.

Определение режима движения жидкости в трубах по числу Рейнольдса:

,

где

– средняя скорость движения жидкости;

d – диаметр трубы – характерный линейный размер потока;

– кинематический коэффициент вязкости жидкости;

Q – расход жидкости.

Принимается расход жидкости в трубе 0 равным ,

тогда

.

Для трубы 0 средняя скорость движения жидкости: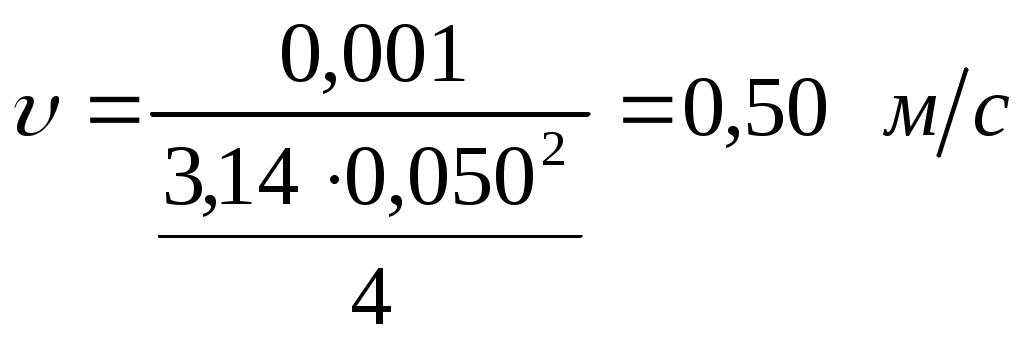

,

тогда число Рейнольдса:

.

Для труб 1 и 2 средняя скорость движения жидкости: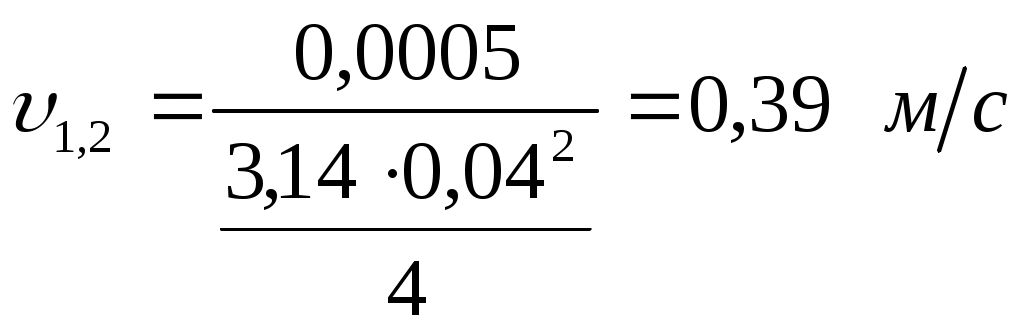

,

тогда

При рас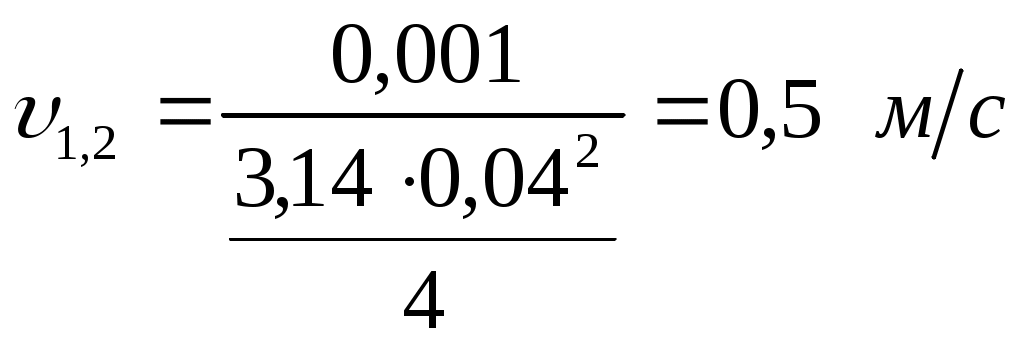ход в трубах 1 и 2 равен

.

0:

;

и 2: ; .

Принимается , т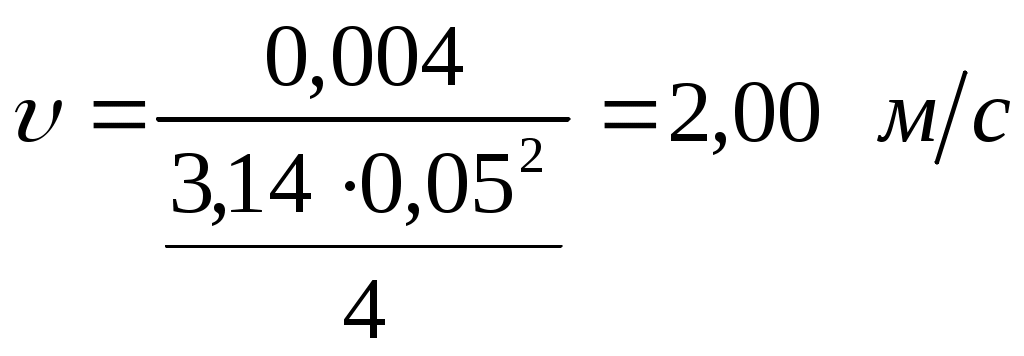огда:

.

0:

;

.

1 и 2:

;

Определяется коэффициент сопротивления трения в зависимости от зоны турбулентного режима.

При и

, в результате

Такое соотношение соответствует доквадратичной зоне сопротивления турбулентного режима. Коэффициент сопротивления трения находится по формуле Альтшуля:

1,2:

, в результате

При и

, в результате

1,2:

, в результате

При и

, в результате

1,2:

, в результате

Такое соотношение соответствует квадратичной зоне сопротивления турбулентного режима. Коэффициент сопротивления трения находится по формуле Шифринсона:

Во всех случаях число Рейнольдса находится в пределах

. Значит, для всех случаев выбирается доквадратичная зона сопротивления турбулентного режима.

Вычисляются потери напора по длине в каждой трубе при всех значениях расходов при помощи формулы Дарси - Вейсбаха:

,

где

- коэффициент сопротивления трения;

l – длина участка трубы;

d – диаметр трубы;

- средняя скорость движения жидкости в сечении трубы.
1. При

;

Для трубы 0 потери напора по длине:

м. в. ст.;

для труб 1 и 2 потери напора по длине соответственно:

м. в. ст.;

м. в. ст.;
2. При

;

Для трубы 0 потери напора по длине:

м. в. ст.;

для труб 1 и 2 потери напора по длине соответственно:

м. в. ст.;

м. в. ст.;
3. При

;

Для трубы 0 потери напора по длине:

м. в. ст.;

для труб 1 и 2 потери напора по длине соответственно:

м. в. ст.;

Запишем уравнение Бернулли для сечений 0-0 и 1-1 относительно плоскости сравнения А – А:

,

где

суммарные потери по длине;

скоростной напор.

Пренебрегаем величиной скоростного напора на выходе из труб 1 и 2 вследствие его относительной малости по сравнению с потерями по длине.

Тогда для всех труб сведем в таблицы полученные характеристики.
Для трубы 0:

Q, м ³/с	0,001	0,002	0,004
	0,50	1,02	2,00
Re	10000	20380	40000
	0,02188	0,03681	0,03681
Н, м. гл. ст.	0,0944	0,399	1,59

Для трубы 1:

Q,м ³/с	0,0005	0,001	0,002
	0,39	0,5	1,59
Re	6369	8152	31800
	0,029	0,0349	0,0349
Н, м. гл. ст.	0,0799	0,472	1,889

Для трубы 2:

Q,м ³/с	0,0005	0,001	0,002
	0,39	0,5	1,59
Re	19840	8152	31800
	0,02616	0,0346	0,0346
Н, м. гл. ст.	0,149	0,564	2,258

График зависимости

имеет вид:

По графику видно, что расход жидкости, протекающей по трубопроводу в пункты 1 и 2, при постоянном напоре в 2,225 м равен, соответственно:

для трубы 1: Q₁= 0,002180 м³/с;

для трубы 2: Q₂ = 0,002082 м³/с ;

для трубы 0: Q₀ = 0,004262 м³/с.

График линии полного напора и пьезометрической линии имеет вид:

Литература.
1. Р.Ю. Акчурин. Гидравлика: Расчетно-графические работы. – Киров: Изд-во ГОУ ВПО «ВятГУ», 2009. – 44с.

2. Примеры расчетов по гидравлике. Учебное пособие для вузов/Под ред. А.Д. Альтшуля. - М.:Стройиздат, 1976. - 255 с.

3. Справочник по гидравлическим расчетам. Под редакцией П.Г. Киселева. Изд. 4-е, переработ. и доп. М., 1972.

4. Курс лекций по гидравлике. Акчурин Р.Ю.