Задача 1. Задача Определить заряд
 Скачать 58.03 Kb. Скачать 58.03 Kb.
|
|
Задача 1.1. Определить заряд Q, прошедший по проводу с сопротивлением R = 3,11Ом при равномерном нарастании напряжения на концах провода от U0 = 1,73 В до U = 5,49В в течение t = 20,31 сек и заряд Q1, прошедший по проводу за первые 5 сек. Решение. Так как сила тока в проводе изменяется, то воспользоваться для подсчёта заряда формулой Q = It нельзя. Поэтому возьмём дифференциал заряда dQ = Idt и проинтегрируем: 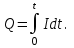 (1) (1) Выразив силу тока по закону академика Петрова-Ома, получим 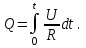 (2) (2)Напряжение U в данном случае переменное, оно зависит от времени. В силу равномерности нарастания оно может быть выражено формулой U = U0+kt, (3) где k - коэффициент пропорциональности. Подставив выражение (3) для U в формулу (2), найдём 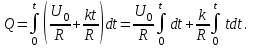 Проинтегрировав, получим 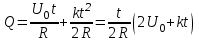 (4) (4)Значение коэффициента пропорциональности k найдём из формулы (3), если заметим, что по условию задачи t = 20,31 с, U = 5,49 В U0 = 1,73В: k = (U - U0) / t = (5,49-1,73)/20,31 = 0,19 B/c. Подставив значения величин вформулу (4), найдём Q = 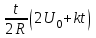 = = 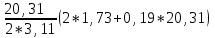 =23,90Кл. =23,90Кл.Заряд Q1, прошедший по проводу за первые 5 сек, равен Q1 = 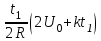 = = 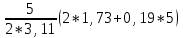 =3,55Кл. =3,55Кл. 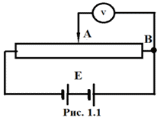 Рис. 1.1 Задача 1.2. Потенциометр с сопротивлением RП= 100Ом подключён к источнику тока, ЭДС Е которого равна 150 В и внутреннее сопротивление r = 50 Ом (рис. 1.1). Определить показание вольтметра с сопротивлением RB=500Ом, соединённого проводником с одной из клемм потенциометра и подвижным контактом с серединой обмотки потенциометра. Какова разность потенциалов между теми же точками потенциометра при отключённом вольтметре? Решение. Показание U1 вольтметра, подключённого к точкам А и В (рис. 1.1), определяется по формуле U1 = I1 R1, (1) где I1 - сила тока в неразветвленной, части цепи; R1 – сопротивление параллельно соединённых вольтметра и половины потенциометра. Силу тока I1 найдём по закону академика Петрова-Ома для всей цепи: I1 = Е / (R+r), (2) где R - сопротивление внешней цепи. Внешнее сопротивление R есть сумма двух сопротивлений: R = RП / 2 + R1. (3) Сопротивление R1, то есть сопротивление двух параллельно соединённых потребителей, а именно вольтметраRB и второй половины потенциометра R/2. Это сопротивление может быть найдено по формуле для проводимостей 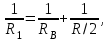 откуда откудаRl= R RB / (R + 2RB). 1. Подставив в эту формулу числовые значения величин, и произведя вычисления, найдём Rl = 45,5Ом. 2. Подставив в выражение (2) правую часть равенства (3), определим силу тока: 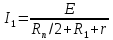 = 1,03 А = 1,03 А3. Если подставить значения I1 и R1в формулу (1), то найдём показание вольтметра: U1 = 46,88В. 4. Разность потенциалов UАВ между точками А и В при отключённом вольтметре равна произведению неизвестного тока I3 в новой неразветвленной части цепи, на половину сопротивления потенциометра, т. е. UАВ = I3 RП/2.Ток I3 в новой неразветвленной части цепи равен I3 = Е / (RП + r), следовательно выражение для разности потенциалов или для напряжения UАВ между точками А и В имеет вид UАВ = Е RП / (RП + r)/2 Подставив сюда значения величин ε, rи RПполучим UАВ = 50В.  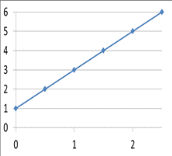 Рис. 1.2 Пример 1.3. Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течение времени Δt = 2,5 с по линейному закону от I0 = 1 до Imax = 6 А (рис. 1.2). Определить количество теплоты Q1, выделившееся в этом проводнике за первую секунду, и Q2 - за оставшееся время, а также найти отношение этих количеств теплоты Q2/Q1. Решение. Закон Джоуля - Ленца Q = I2Rt применим в случае постоянного тока (I= const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде производной по времени dQ = I2R dt. (1) Здесь сила тока I является некоторой функцией времени. В нашем случае – линейной I = I0+kt, (2) где k - коэффициент пропорциональности, равный отношению приращений силы тока к интервалу времени, за который произошло это приращение: k = ΔI/Δt. С учётом равенства (2) формула (1) примет вид dQ = R (I0+kt)2 dt. (3) Для определения количества теплоты, выделившегося за конечный промежуток времени Δt = t2 - t1, выражение (3) следует проинтегрировать в пределах от t1до t2: 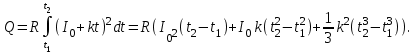 При определении количества теплоты, выделившегося за первую секунду, пределы интегрирования t1= 0, t2 = 1 с и, следовательно, Q1 = 86,67 Дж, а за оставшееся время - пределы интегрирования t1 = 1 с, t2 = 2,5 с и тогда Q2 = 630 Дж. Следовательно, Q2/Q1 = 7,27, т. е. за оставшееся время выделится теплоты в 7,27 раз больше, чем за первую секунду. |
