№ п/п
|
Задача
|
Ответ
|
1.
|
Вычислить определённые интегралы. Для несобственных интегралов решить вопрос об их сходимости или расходимости:
|
|
Условие задачи:
а) 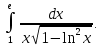
|
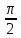
|
Подробное решение:
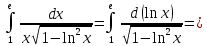
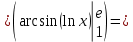
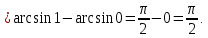
|
№ п/п
|
Задача
|
Ответ
|
1.
|
Условие задачи:
б) 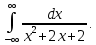
|
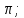
сходится
|
Подробное решение:
Воспользуемся формулой для несобственного интеграла с двумя бесконечными пределами интегрирования:
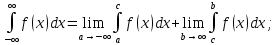
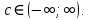
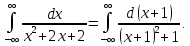
Пусть  Тогда Тогда
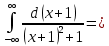
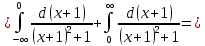
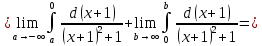
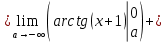
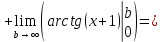
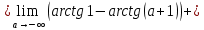
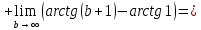
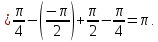
Следовательно, заданный несобственный интеграл сходится.
|
№ п/п
|
Задача
|
Ответ
|
1.
|
Условие задачи:
в) 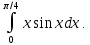
|
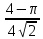
|
Подробное решение:
При вычислении интеграла применим метод интегрирования по частям, по которому интеграл вычисляется с помощью следующей формулы:
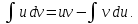
Пусть 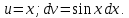 Тогда Тогда
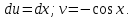
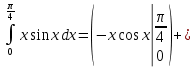
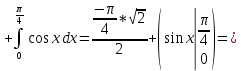
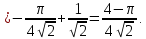
|
№ п/п
|
Задача
|
Ответ
|
1.
|
Условие задачи:
г) 
|
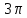
|
Подробное решение:
Применим подстановку:
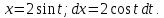
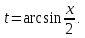
Тогда
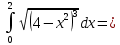
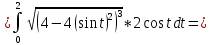
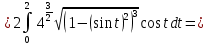

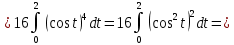
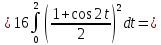
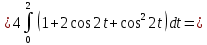
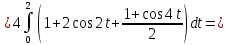
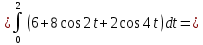
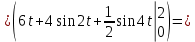
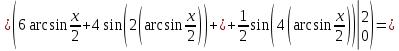
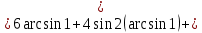
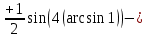
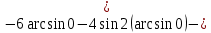
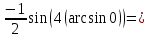
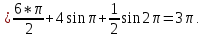
|
№ п/п
|
Задача
|
Ответ
|
2.
|
Сделать чертеж области, ограниченной заданными линиями. Вычислить площадь полученной фигуры:
|
|
Условие задачи:
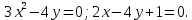
|
8/27
|
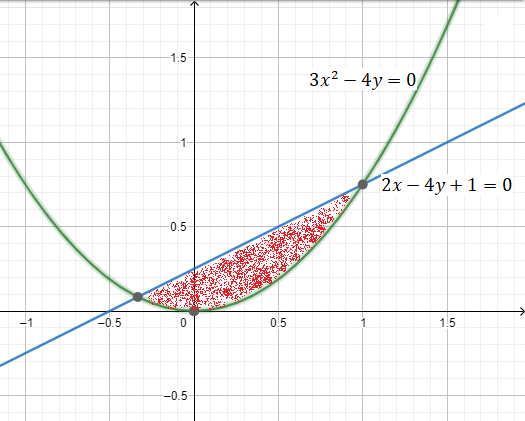
Чертёж области:
|
Подробное решение:
Линии из условия задачи можно выразить в явном виде:
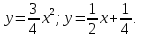
Найдем точки пересечения этих линий.
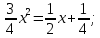
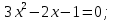
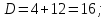
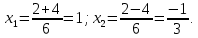
Следовательно, площадь фигуры, закрашенной на чертеже красным цветом, можно вычислить как определенный интеграл разности двух заданных функций на отрезке 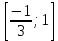 . .
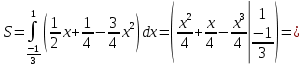
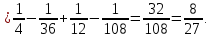
|
|
 Скачать 54.85 Kb.
Скачать 54.85 Kb.