РЗ векторный анализ. расчетные задачи векторный анализ Оболенков. Задача Ответы 8 Векторный анализ задача 1, задача 2, задача 4, задача 5, задача 7, задача 10

• Название: Задача Ответы 8 Векторный анализ задача 1, задача 2, задача 4, задача 5, задача 7, задача 10
• Анкор: РЗ векторный анализ
• Дата: 04.05.2023
• Размер: 379.5 Kb.
• Имя файла: расчетные задачи векторный анализ Оболенков.doc
• Тип: Задача; #1107998

Кратные интегралы: задача 8.

Ответы: 8) 6.

Векторный анализ: задача 1, задача 2, задача 4, задача 5, задача 7, задача 10

Ответы: 1)0; 2) ; 4) 0; 5) 7; 7) ; 10) .
Кратные интегралы

Задача 8. Пластинка задана ограничивающими ее кривыми, -поверхностная плотность. Найти массу пластинки.

12.

Решение: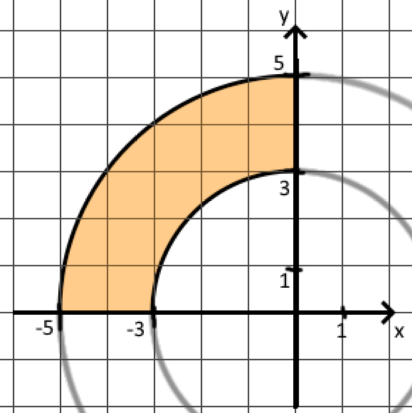



Рисунок 1 – Ограниченная область

Масса пластинки:



Пусть 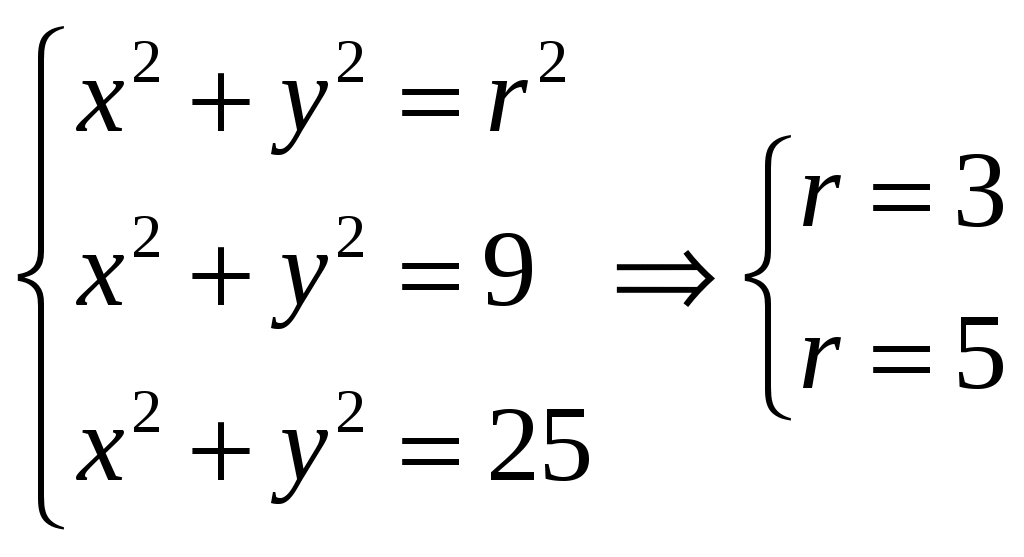, . Тогда ,



Следовательно,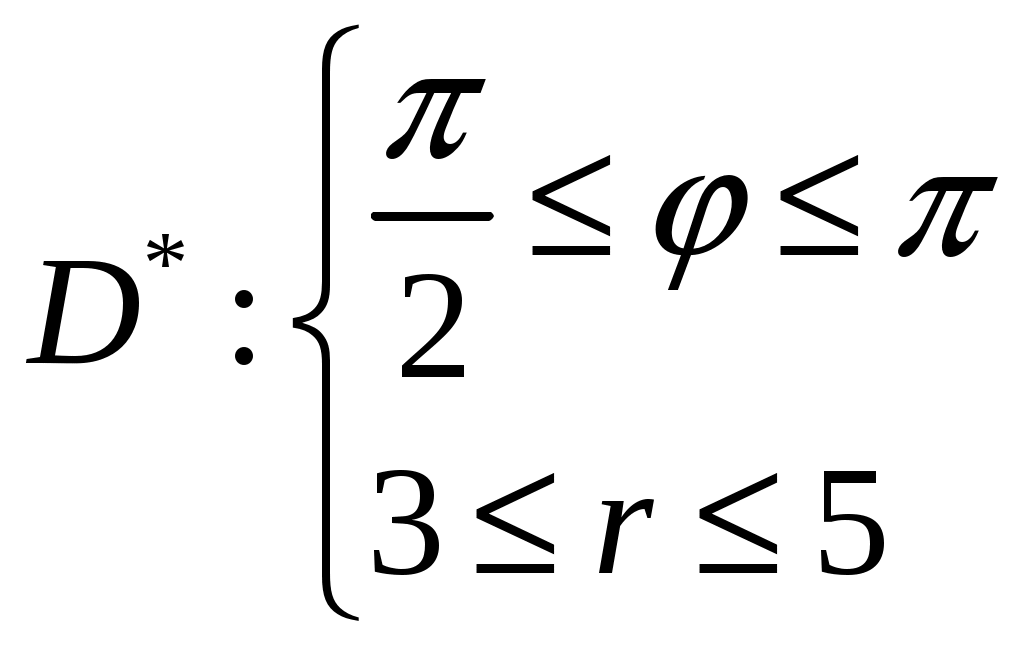



Масса пластинки: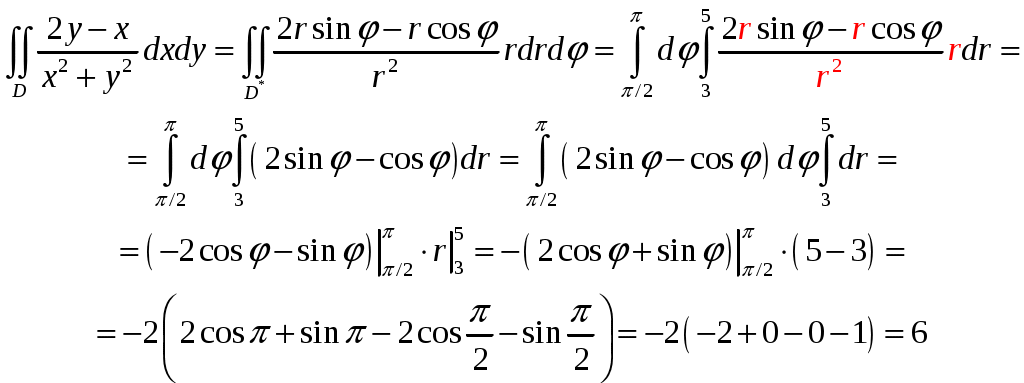



Ответ: 6.

Векторный анализ

Задача 1. Найти производную скалярного поля в точке по направлению проходящей через эту точку нормали к поверхности , образующей острый угол с положительным направлением оси .

12.

Решение:

Уравнение поверхности

Нормальный вектор S имеет вид

Найдем частные производные функции S:



Частные производные функции S в точке M:



Тогда нормальный вектор S и его длина:





Направляющие косинусы:



Найдем частные производные поля u в точке M: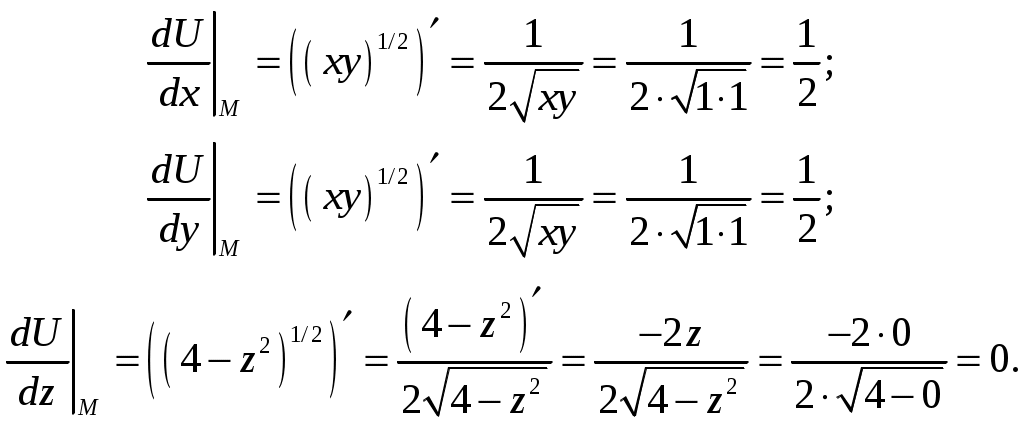



Следовательно,



Ответ: 0.

Задача 2. Найти угол между градиентами скалярных полей и в точке .

12.

Решение:
Найдем частные производные поля u в точке M: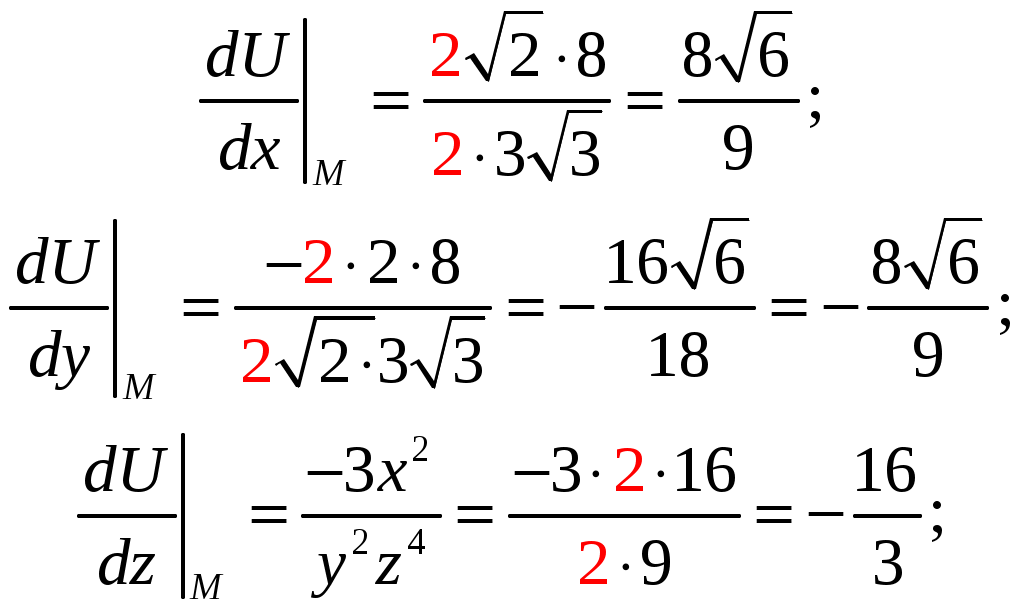





Тогда: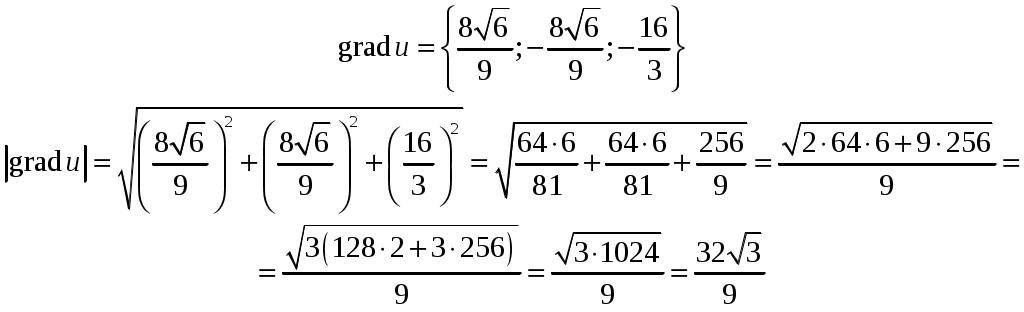



Найдем частные производные поля v в точке M:





Тогда: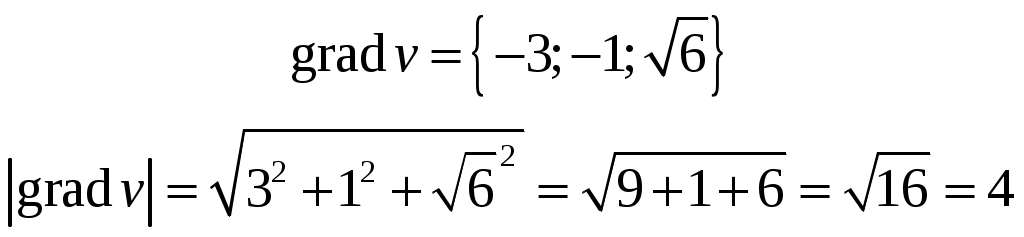



Так как





То: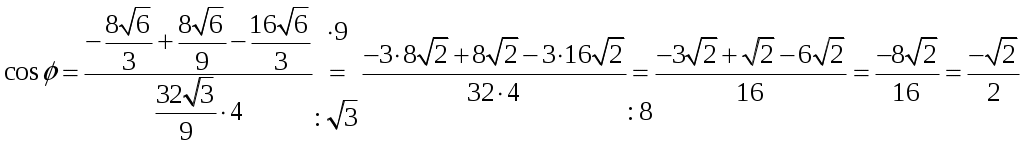





Ответ:

Задача 4. Найти поток векторного поля через поверхности , вырезаемую плоскостью (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).

12.

Решение: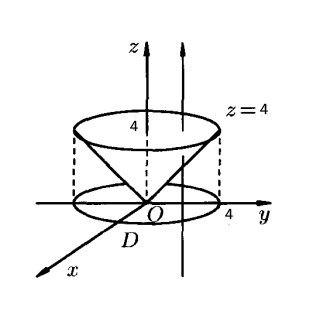



Рисунок 2 – Замкнутая поверхность (рисунок взят из учебника)

Для нахождения потока векторного поля через замкнутую поверхность в направлении внешней нормали воспользуемся формулой Остроградского-Гаусса. Для этого найдем дивергенцию векторного поля:





Ответ: 0.

Задача 5. Найти поток векторного поля a через часть плоскости , расположенную в первом октанте (нормаль образует острый угол с осью .

12.

Решение: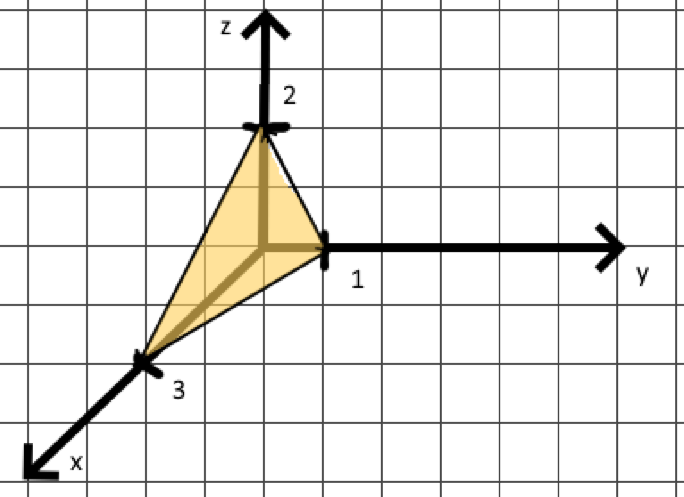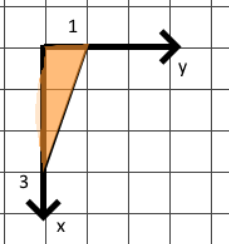



Рисунок 3 – Ограниченная плоскость и ее проекция

Поток векторного поля через плоскость – поверхностный интеграл:



Нормальный вектор плоскости



Тогда







Выразим уравнение плоскости через z и перепишем поверхностный интеграл в виде двойного:





Вычислим частные производные z: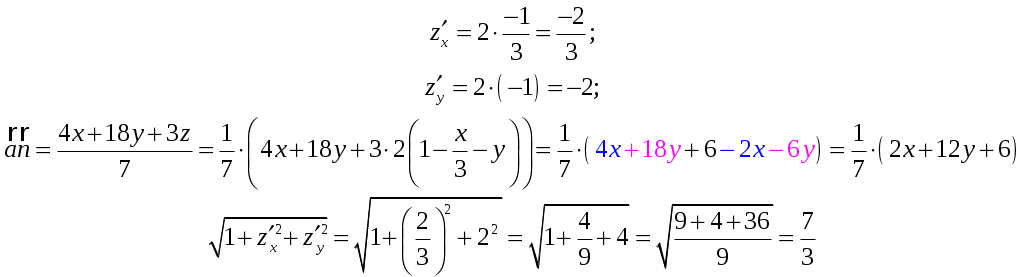

Уравнение проекции:




Тогда:



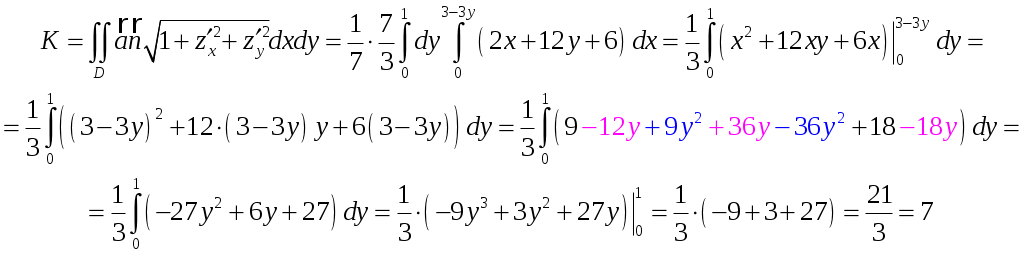Ответ: 7.

Задача 7. Найти поток векторного поля через замкнутую поверхность (нормаль внешняя).

12.
Решение: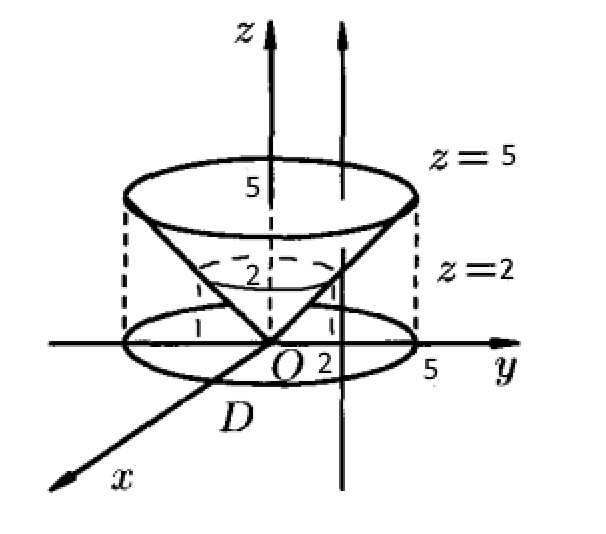



Рисунок 2 – Замкнутая поверхность (рисунок взят из учебника)

Для нахождения потока векторного поля через замкнутую поверхность в направлении внешней нормали воспользуемся формулой Остроградского-Гаусса. Для этого найдем дивергенцию векторного поля:





Перейдем к цилиндрическим координатам: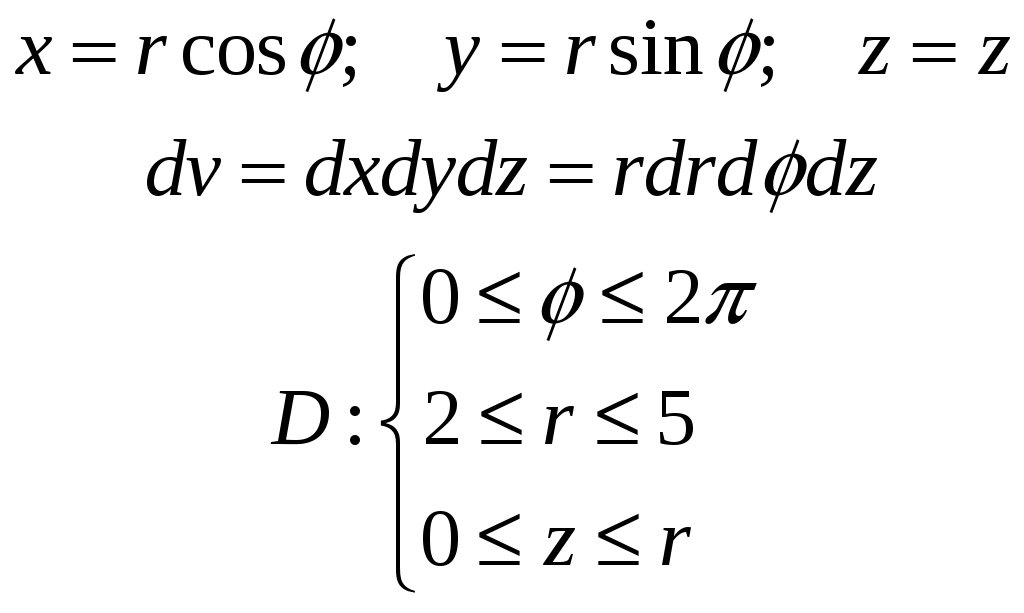



Тогда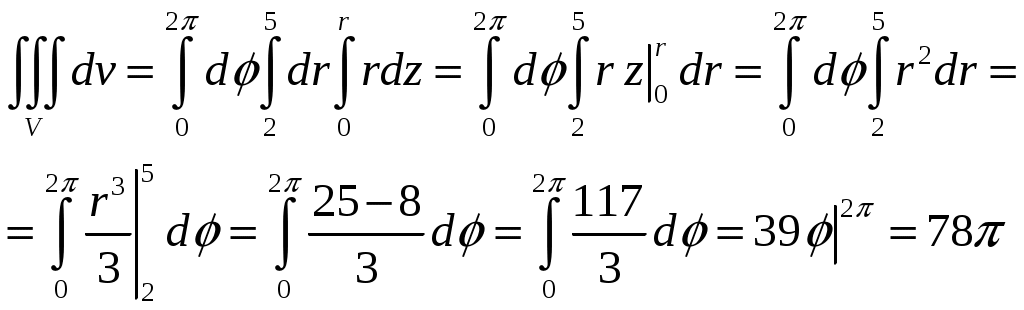



Ответ:

Задача 10. Найти работу силы при перемещении вдоль линии от точки к точке .

12.

Решение: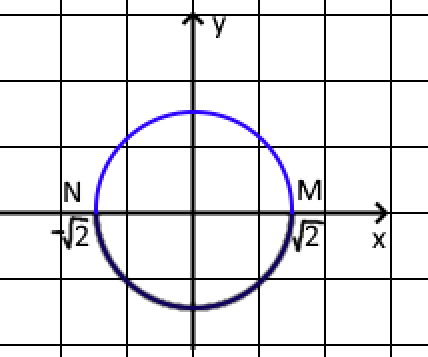



Рисунок 4 – График перемещения

Выразим y в уравнении прямой:



Посчитаем работу силы: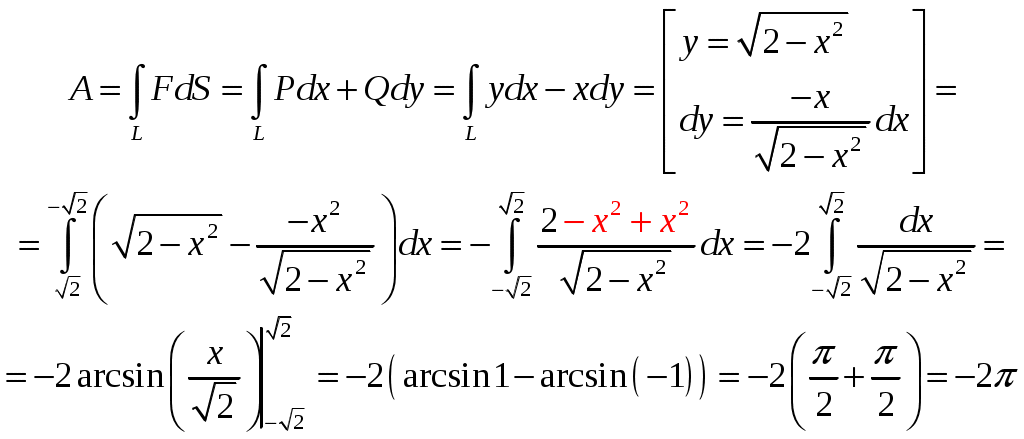



Ответ: