Вариант 1+. Задача По группе грузовых автотранспортных предприятий города имеется следующая информация за отчетный год
 Скачать 443.53 Kb. Скачать 443.53 Kb.
|
|
Вариант№1 Задача 1. По группе грузовых автотранспортных предприятий города имеется следующая информация за отчетный год:
Произведите группировку грузовых автотранспортных предприятий по размеру грузооборота, разделив на три группы. По каждой группе рассчитайте среднюю величину затрат. Оформите результаты в виде таблицы с соответствующим названием. Сделайте соответствующие выводы. Произведем группировку по размеру грузооборота. Определим величину интервала по формуле h = Xmax – Xmin/n 62-15/3=15 1 группа - 15-30 (8 предп.) 2 группа – 31-46 (4 предп.) 3 группа – 47-62 (4 предп.) Таблица - группировка грузовых автотранспортных предприятий по размеру грузооборота.
Средняя величина затрат по каждой группе: 1 группа – 5480/8 = 685 2 группа – 4147/4 = 1036,7 3 группа – 5549/4 = 1387,2 Вывод: произведя подсчет, мы можем видеть, что 1 группа является самой многочисленной по числу предприятий, однако по средней величине затрат на перевозки в среднем на одно предприятие 1 группу превосходит третья, как и по грузообороту. По грузообороту 3 группа превосходит первую и вторую. Задача №2 1. Определить общее производство моющих средств в условных тоннах (условная жирность 40%) по плану и фактически, а также процент выполнения плана по следующим данным:
Решение. Учитывая условную жирность 40%, определим количество производства моющих средств в условных тоннах каждого вида по плану (X’1i) и фактически (X1i): – мыло хозяйственное: X’1мх = 60/40*500 = 750 у.т. мыло хозяйственное X1мх = 60/40*600 = 900 у.т.; – мыло туалетное: X’1мт = 80/40*1000 = 2000 у.т. мыло туалетное: X1мт = 80/40*1500 = 3000 у.т.; – стиральный порошок: X’1сп = 10/40*50000 = 12500 у.т. – стиральный порошок: X1сп = 10/40*40000 = 10000 у.т. Суммируя количество производства моющих средств в условных тоннах каждого вида, получим общее количество в условных тоннах моющих средств: – по плану X’1= X’1i= 15250 у.т.; – фактически X1= X1i= 13900 у.т. Процент выполнения плана производим по формуле: V факт * 100 \ v план. 600*100\500=120% - мыло хоз. 1500*100\1000=150% - мыло туал. 40000*100\50000=80% - стир. порошок Задача №3 Постройте радиальную диаграмму по данным о производстве шоколада и шоколадных изделий по одному из кондитерских изделий по месяцам 2018 года (в т)
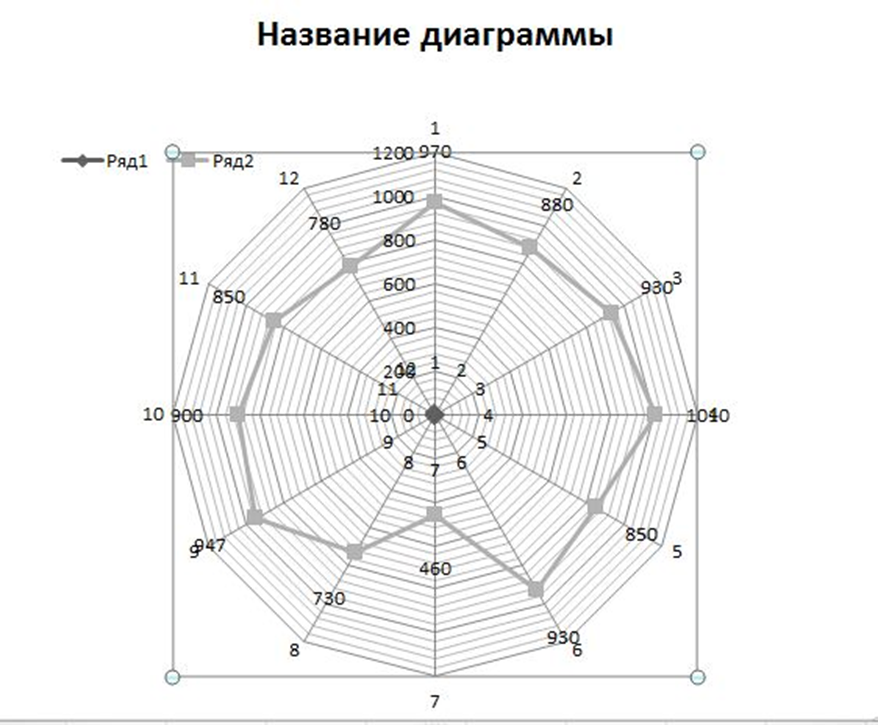 Задача №4 В прошлом году объём грузооборота по грузовому автотранспортному предприятию составил 310 млн. т/км. Планом текущего года было предусмотрено довести объём грузооборота до 320,5 тыс. т/км. Фактический объём грузооборота в текущем году составил 329,32 млн. т/км. Определить: относительную величину планового задания по росту грузооборота; относительную величину динамики грузооборота; относительную величину выполнения плана по грузообороту. Решение: 1) относительная величина планового задания по росту грузооборота: ОВПЗ= 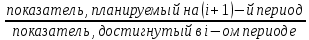 = =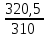 х100=103,0% х100=103,0%Следовательно по плану предусмотрено увеличение грузооборота на 3% (103-100) 2) относительная величина динамики грузооборота: ОВД= 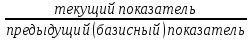 х 100% = х 100% = 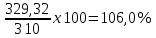 Следовательно, фактически по сравнению с прошлым годом грузооборот повысился на 6% (106-100) 3) относительная величина выполнения плана по грузообороту: ОВВП=  Т.е. план по размеру грузооборота превышен на 4% (106-102) Задача№ 5 Дан ряд чисел:18; 15; 22; 15; 12; 14;15; 13. Найдите размах, среднее арифметическое, медиану и моду этого ряда. Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел 22-12= 10 Среднее арифметическое данного ряда находим по формуле средней арифметической простой. Хср 18+15+22+15+12+14+15+13/8 = 15,5 Для определения медианы необходимо предложенный ряд упорядочить – расположить числа, например, в порядке возрастания: 12;13;14;15;15;15;18;22 Медиана четного ряда чисел находится путем вычисления средней арифметической двух цифр, стоящих посередине ряда: Ме = 15+15/2 = 15 Мода дискретного ряда чисел – это число, которое встречается в данном ряде чаще других. Мо = 22 Задача 6. По данным обследования получено следующее распределение студентов-заочников по возрасту на разных факультетах.
Рассчитайте на экономическом факультете: ♦ средний возраст студента-заочника; ♦ модальное значение; ♦ медиану. В данном ряду варианты усредняемого признака (возраст студента) представлены не одним числом, а в виде интервала «от – до». Причём последний – интервал открытый. В таких рядах условно принимается, величина интервала последней группы равна величине интервала предыдущей. Таким образом, возраст студента в последней группе равен 45-49 Исчисление средней по сгруппированным данным производится по формуле средней арифметической взвешенной: 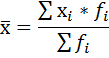 Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. 20+25/2 = 22,5 26+30/2 = 28 31+35/2 = 33 36+40/2 = 38 45+49/2 = 47
Дальнейший расчёт производится обычным методом определения средней арифметической взвешенной: Х= Σxf\Σf 282730/9980 = 28,3 Средний возраст студента-заочника на экономическом факультете равен 28,3 годам. модальное значение В интервальных рядах распределения с равными интервалами мода определяется по формуле: 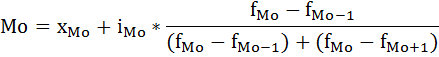 xMo – начальное значение интервала, содержащего моду; iMo – величина модального интервала, fMo – частота модального интервала, f(Mo-1)– частота интервала, предшествующего модальному, f(Mo+1) – частота интервала, следующего за модальным. Сначала определим модальный интервал: Наибольшее число студентов 9000, возраст студентов 26-30. Следовательно, этот интервал является модальным интервалом ряда распределения. xMo – 26 iMo – 4 fMo – 9000 f(Mo-1) - 200 f(Mo+1) - 700 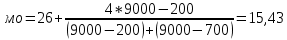 ♦ медиана Медиана интервального вариационного ряда распределения определяется по формуле: 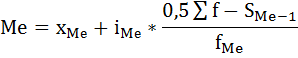 где xMе– начальное значение интервала, содержащего медиану; iMе – величина медианного интервала; Σf – сумма частот ряда; S(Me-1)– сумма накопленных частот, предшествующих медианному интервалу; fMe– частота медианного интервала. Определим, прежде всего, медианный интервал. Сумма накопленных частот, превышающая половину всех значений (9200 ), соответствует интервалу 26-30. Это и есть медианный интервал, в котором находится медиана. xMе – 26 iMе – 4 Σf – 9980 S(Me-1) - 200 fMe - 9000 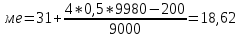 Задача 7 Информация о вкладах в банке
Определить средний размер вклада по двум видам. Решение: 1) Пусть в октябре известен средний размер вкладов каждого вида и число вкладов. По формуле средней арифметической взвешенной: 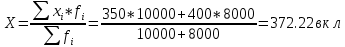 2) Пусть в ноябре известен средний размер вкладов каждого вида и сумма вкладов. По формуле средней гармонической взвешенной: 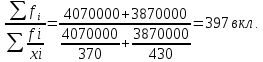 Теоретический вопрос: Что такое статистическое исследование, какие стадии оно проходит (3 стадии)? Какие стадии (этапы) включает в себя статистическое наблюдение? Статистическое исследование количественной стороны общественных явлений проходит три стадии. 1. На первой стадии с помощью проведения статистического наблюдения собирают статистические данные, характеризующие социально-экономические явления. 2. На второй стадии статистического исследования собранные данные подвергаются сводке и группировке. Важнейшим методом на второй стадии статистической сводки является метод группировок, позволяющий выделить однородные совокупности, разделить их на группы и подгруппы. На этой стадии переходят от описания отдельных единиц к описанию их групп и объекта в целом посредством подсчета итогов, вычисления обобщающих показателей в виде относительных средних величин. 3. Третья стадия статистического исследования состоит в анализе и обобщении статистических фактов обнаружении закономерностей в изучаемых явлениях. Здесь применяется весь арсенал статистических методов - это ряды динамики, индексы, методы математической статистики и т. д. Выводы и анализ излагаются в текстовой форме и сопровождаются таблицами и графиками. Этапы проведения статистического наблюдения: подготовка наблюдения; проведение массового сбора данных; подготовка данных наблюдения к обработке; разработка предложений по совершенствованию проведения статистического наблюдения. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
