Кр. Контроша статистика. Задача По группе магазинов города имеются следующие данные за отчетный период Номер магазина

Название	Задача По группе магазинов города имеются следующие данные за отчетный период Номер магазина
Дата	16.01.2022
Размер	56.68 Kb.
Формат файла
Имя файла	Контроша статистика.docx
Тип	Задача #332700

ВАРИАНТ 3

Задача 3.1.

По группе магазинов города имеются следующие данные за отчетный период:

Номер магазина	Годовой товарооборот, ден. ед.	Среднесписочное число работающих, чел.	Издержки обращения, ден. ед.
1	1226 +α	21+α	66+α
2	2875 -β	64-β	162-β
3	2410+β	45+β	120+β
4	2456-β	45-β	125-β
5	1864+2α	34+α	106+α
6	802-2α	38-α	42-α
7	2692+2β	53+β	140+β
8	2475-2β	41-β	115-β
9	2432+α	48+α	118+α
10	1092-β	33-β	64-β
11	2443+β	45+β	140+β
12	1816-β	34-β	102-β
13	2312+2α	43+α	125+α
14	1068-2α	32-α	88-α
15	1254+2β	23+β	60+β
16	2662-2β	48-β	130-β
17	918+α	20+α	52+α

По данным таблицы произвести группировку предприятий по размеру товарооборота, выделив 4 группы.

Установить зависимость издержек обращения от товарооборота и среднесписочной численности работников. Сделать выводы.

Решение

№ п/п	Годовой товарооборот, ден. ед	Среднесписочное число работающих, чел.	Издержки обращения, ден. ед.
1	1234	29	74
2	2867	76	154
3	2418	53	128
4	2448	37	117
5	1880	42	124
6	818	30	34
7	2708	61	148
8	2459	39	107
9	2440	56	126
10	1084	25	56
11	2451	53	148
12	1808	26	94
13	2328	51	133
14	1052	24	80
15	1270	31	68
16	2646	40	122
17	934	28	60

Рассчитываем размах вариации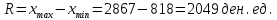

Вариация этого признака значительна, рассчитаем величину интервала при равных интервалах по формуле: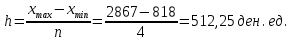

Xmax - максимальное значение группированного признака в совокупности.

Xmin - минимальное значение группировочного признака.

Интервалы:

818 - 1330,25

1330,25 - 1842,5

1842,5 - 2354,75

2354,75 - 2867

Результат группировки

Группы по товарообороту, ден.ед.	Коли чество пред приятий, ед.	Годовой товарооборот, ден. ед.		Среднесписочное число работающих, чел.		Издержки обращения, ден. ед.
Группы по товарообороту, ден.ед.	Коли чество пред приятий, ед.	всего	в среднем на 1 предприятие	всего	в среднем на 1 предприятие	всего	в среднем на 1 предприятие
802 - 1330,25	6	6392	1065,3	167	27,8	372	62
1330,25 - 1842,5	1	1808	1808	26	26	94	94
1842,5 - 2354,75	2	4208	2104,0	93	46,5	257	128,5
2354,75 - 2867	8	20437	2554,6	415	51,87	1050	131,25
Итого	17	32845	1932,1	701	41,2	1773	104,3

Как видно из таблицы с ростом товарооборота увеличивается численность работников и сумма издержек обращения.
Задача 3.2.

На заводе проведено обследование затрат времени на обработку одной детали. Получены следующие данные:

Затраты времени на одну деталь, мин	Число рабочих, чел.
до 24	2+α
24-26	12+β
26-28	34+α
28-30	40+β
30-32	10+α
32-34	2+β

Исчислите средние и показатели вариации затрат времени на одну деталь:

среднюю величину;

среднее линейное отклонение;

среднее квадратическое отклонение;

коэффициент вариации;

5) моду;

6) медиану.

Поясните значение каждого показателя.

Решение

Затраты времени на одну деталь, мин	Число рабочих, чел.	Середина интервала, х	хf	накопленная частота	(xi-xcp)2	(xi-xcp)2*fi	\|xi-xcp \|	\| xi-xcp \|f
до 24	10	23	230	10	25	250	5	50
24-26	20	25	500	30	9	180	3	60
26-28	42	27	1134	72	1	42	1	42
28-30	48	29	1392	120	1	48	1	48
30-32	18	31	558	138	9	162	3	54
32-34	10	33	330	148	25	250	5	50
	148	168	4144			932		304

Средние затраты времени на одну деталь: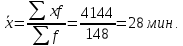

Рабочие в среднем тратят на изготовление одной детали 28 мин.

Среднее линейное отклонение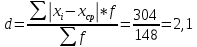

Конкретные значения затрат времени на одну деталь в среднем отклоняются от среднего значения признака на 2,1 минут.

Среднеквадратическое отклонение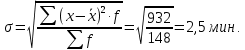

Среднее квадратическое отклонение так же, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняются конкретные значения признака от среднего их значения.

Коэффициент вариации

Коэффициент вариации меньше 33%, значит совокупность однородна. Средние, рассчитанные для однородной совокупности – значимы, т.е. действительно характеризуют эту совокупность.

Мода - значение признака (варианта) наиболее часто встречающегося в изучаемой совокупности. В интервальных вариационных рядах мода определяется по формуле: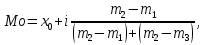

где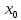

- нижняя граница модального интервала;

i – величина модального интервала;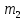

- частота модального интервала;

- частота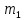 интервала, предшествующего модальному;

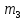– частота интервала, последующего за модальным.

Модальный интервал соответствует наибольшей частоте, это интервал 28-30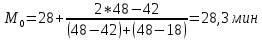

Вывод: наиболее часто встречаются затраты времени на изготовление деталей 28,3 мин.

Медиану рассчитываем по формуле: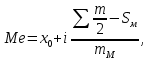

где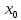

- нижняя граница медианного интервала;

i – величина медианного интервала;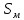

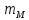- сумма частот до медианного интервала;

– частота медиального интервала.

Медианный интервал будет 28-30 , так как 148/2 = 74, 74-я деталь находится в данном интервале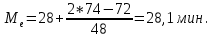

Вывод: половина рабочих на изготовление деталей из совокупности тратит 28,1 мин, а другая половина более 28,1 минут.
Задача 3.3.

На предприятии было проведено выборочное обследование возраста рабочих методом случайного бесповоротного отбора. В результате обследования получены следующие данные:

Возраст рабочих, лет	до 30	30-40	40-50	50-60	свыше 60
Число рабочих	8+2α	22+2β	10+2α	6+2β	4+2α

Определить с вероятностью 0.997 пределы, в которых находится средний возраст рабочих предприятия.
Решение

Возраст рабочих, лет	Число рабочих	Середина интервала	xf
до 30	24	25	600	327,61	7862,6
30-40	38	35	1330	65,61	2493,2
40-50	26	45	1170	3,61	93,86
50-60	22	55	1210	141,61	3115,4
свыше 60	20	65	1300	479,61	9592,2
Итого	130	225	5610		23157

Для собственно-случайной и механической выборки с бесповторным способом отбора средняя ошибка μx выборочной средней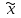

определяется по формуле

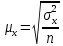где σ2 – общая дисперсия выборочных значений признаков,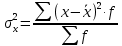

Средний возраст рабочих предприятия: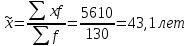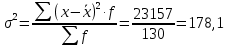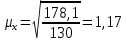

Расчет предельной ошибки выборки

∆=t* μx=3*1,17 = 3,51

Определим пределы, в которых находится средний возраст рабочих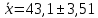

Генеральная средняя (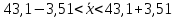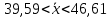

) находится в пределах

С вероятностью 0,997 можно утверждать, что средний возраст рабочих предприятия находится в пределах от 39,59 до 46,61 лет.
Задача 3.4.

По предприятию имеются следующие данные:

Группы рабочих	Число рабочих в группе, чел.
Группы рабочих	выполнивших и перевыполнивших сменное задание	не выполнивших сменное задание
Прошедшие техническое обучение	105 +α	30+α
Не прошедшие техническое обучение	25 +β	60 +β

Установить тесноту связи с помощью коэффициента взаимной сопряженности Чупрова.

Решение

Группы рабочих	Число рабочих в группе, чел.		Итого
	выполнивших и перевыполнивших сменное задание	не выполнивших сменное задание

Прошедшие техническое обучение	a 113	b 38		151
Не прошедшие техническое обучение	c 33	d 68		101
Итого	146	106

Коэффициент взаимной сопряженности Чупрова применяется при наличии признаков 3 и более. а измерение связи при альтернативной вариации двух признаков осуществляется с помощью следующих коэффициентов ассоциации и контингенции.

Коэффициент ассоциации:

Коэффициент контингенции: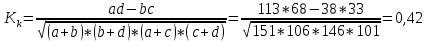

Связь считается подтвержденной, если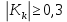

Таким образом связь между рабочими, выполнившими сменное задание и прошедшими техническое обучение тесная, прямая. С увеличением численности рабочих, прошедших обучение увеличивается и численность рабочих выполнивших сменное задание.