Практическое занятие 2. Задача При многократном измерении силы f получены значения в н
 Скачать 338.01 Kb. Скачать 338.01 Kb.
|
|
Решение задач. Задача 1. При многократном измерении силы F получены значения в Н: 98,3; 98; 99,8; 99,9; 98,4; 98; 98,3; 99,1; 98,5; 98,4; 98. Предполагая нормальный закон распределения результатов и отсутствие систематических и грубых погрешностей, укажите доверительные границы истинного значения силы с вероятностью Р = 0.95. Решение: 1. Определяем количество измерений n=11 и вычисляем оценку математического ожидания по формуле: 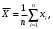 следовательно: 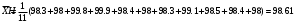 2. Далее находим оценку СКО: 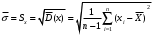 . .Получаем: 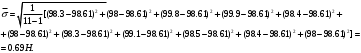 3. Затем находим СКО среднего арифметического: 3. Затем находим СКО среднего арифметического: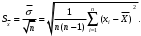 Получаем: 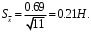 4. Определяем доверительные границы ε случайной погрешности 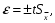 где t – коэффициент Стьюдента (Таблица 1) в зависимости от доверительной вероятности P и числа результатов измерений n. Получаем: 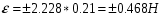 . .5. Получаем ответ: 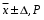 . .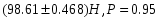 . .6. Округляем по правилам округления и получаем: 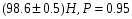 . .Для самостоятельного решения: 1. При многократном измерении сопротивления в электрической цепи получены следующие значения: 703; 708; 705; 699; 710; 705; 707; 698; 703 Ом. Предполагая нормальный закон распределения результатов и отсутствие систематических и грубых погрешностей, укажите доверительные границы истинного значения сопротивления с вероятностью Р = 0,99. Задача 2. Было проведено пять измерений напряжения в электросети. Получены следующие данные: 220,1; 220,2; 219,9; 220,9; 220,2; 220,3 В. Результат 220,9 В существенно (на первый взгляд) отличается от остальных. Проверить по Вариационному критерию Диксона, не является ли он промахом при заданном уровне значимости q= 0.05. Решение: Количество измерений n=6. Составляем вариационный возрастающий ряд вида: 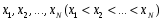 . .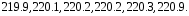 Затем определяем значение критерия: 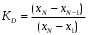 , ,получаем: 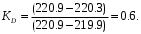 По таблице 2 находим критическое значение критерия при заданном уровне значимости q= 0.05 и количестве измерений n=6: 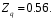 Получаем: 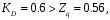 Следовательно, результат 220,9 В является промахом. Задача 3. При многократном измерении частоты f получен ряд измеренных значений: 780.4, 780.2, 780, 780.3, 790.9, 780.3, 780.4, 780 Гц. Используя критерий Граббса, необходимо проверить полученные результаты измерений на наличие грубой погрешности с вероятностью Р=0.99. Решение: 1. Определяем количество измерений n=8 и вычисляем оценку математического ожидания по формуле: 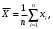 следовательно: 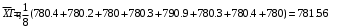 2. Далее находим оценку СКО: 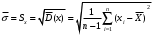 . .Получаем: 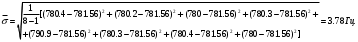 3. Определяем статистики: 3. Определяем статистики: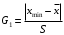 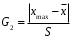 , ,получаем: 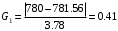 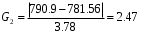 . .4. Определяем по таблице 4 теоретическое значение Gт критерия Граббса при заданном уровне значимости q = 1-P = 0.01: 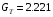 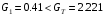 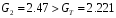 , ,Так как 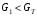 , то , то 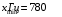 - не является промахом. - не является промахом.Так как 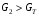 , то , то 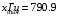 - является промахом. - является промахом.Для самостоятельного решения: 1. При диагностировании топливной системы автомобиля результаты пяти измерений расхода топлива составили: 23, 24, 25, 26, 27, 29 л на 100 км. Последний результат вызывает сомнение. Проверить по критерию Романовского, не является ли он промахом, при уровне значимости q=0.05. 2. При многократном измерении мощности P получен ряд измеренных значений: 40.4, 41, 40.2, 40, 45.5, 42.7, 40.3, 40.4, 40.8, 40.4, 41, 40.2, 40, 33.5, 42.7, 40.4 Вт. Используя критерий Граббса, необходимо проверить полученные результаты измерений на наличие грубой погрешности с вероятностью Р=0.95. Таблица 1. Значения критерия Стьюдента 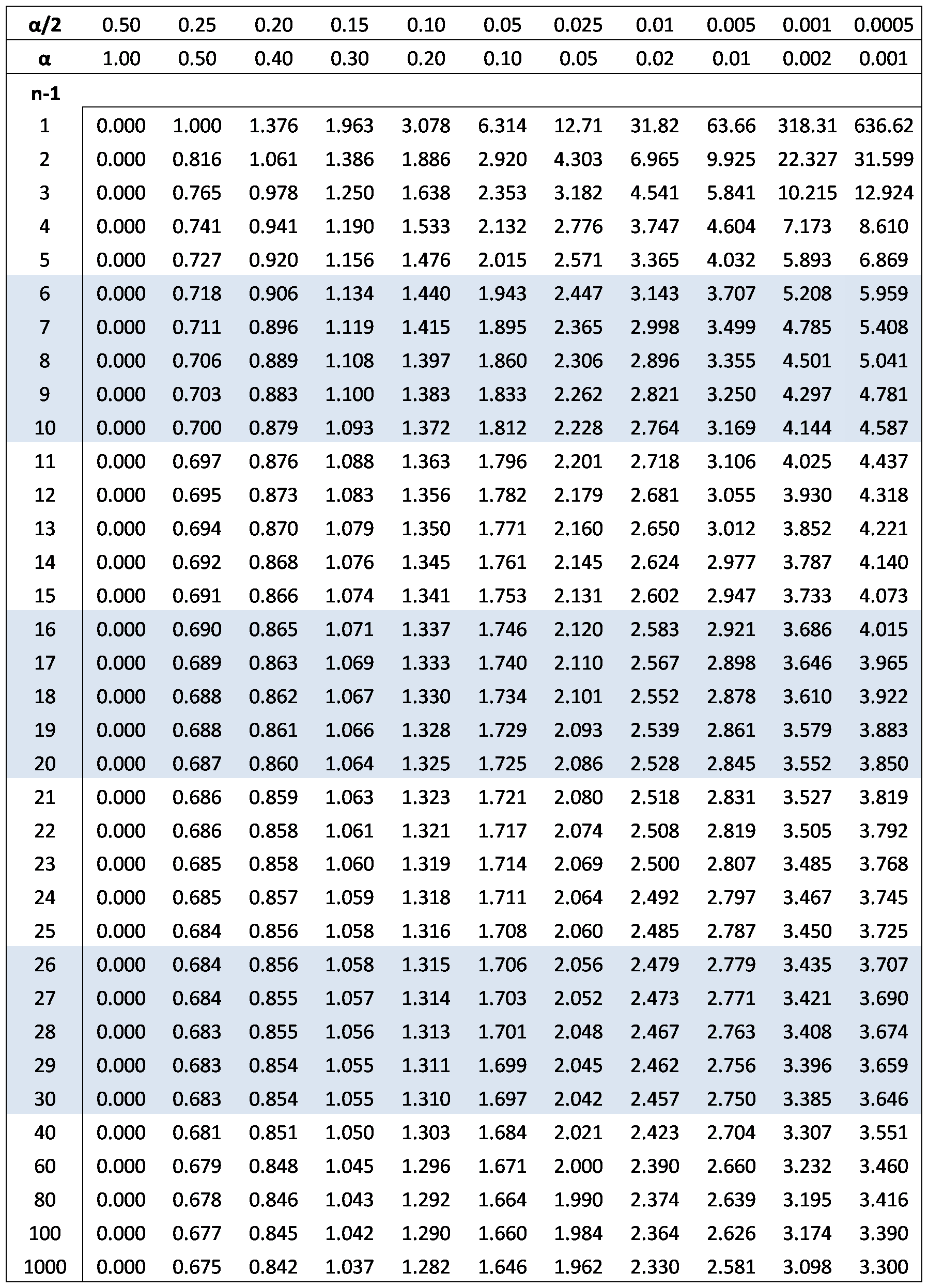 Таблица 2. Значения критерия Диксона
Таблица 3. Значения критерия Романовского
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
