Задача При внезапной остановке насоса за счет сжатия жидкости в объеме напорного трубопровода диаметром и длиной поступило жидкости
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
Практическая частьЗадача 1. При внезапной остановке насоса за счет сжатия жидкости в объеме напорного трубопровода Определить величину давления в трубопроводе в момент остановки насоса, если до его остановки давление в трубопроводе составляло 0,6 МПа. Коэффициент объемного сжатия жидкости Решение 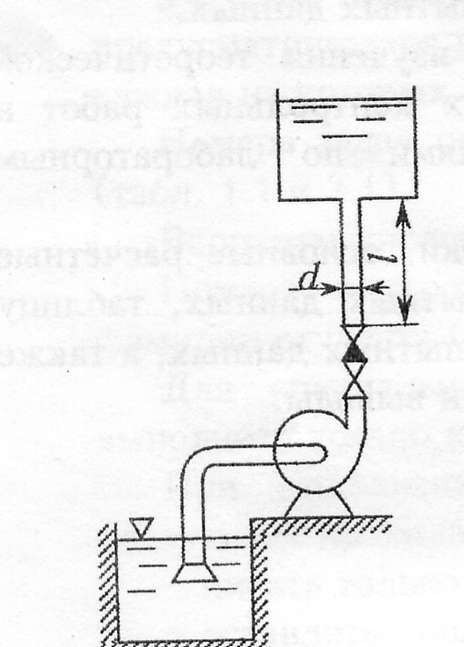 Коэффициент объемного сжатия 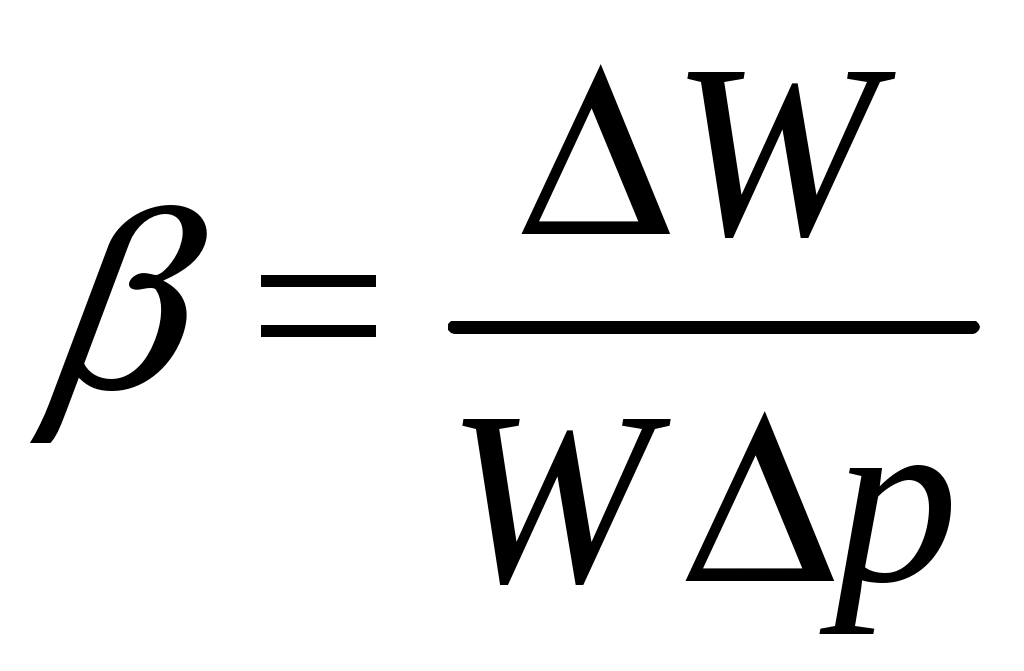 , ,где 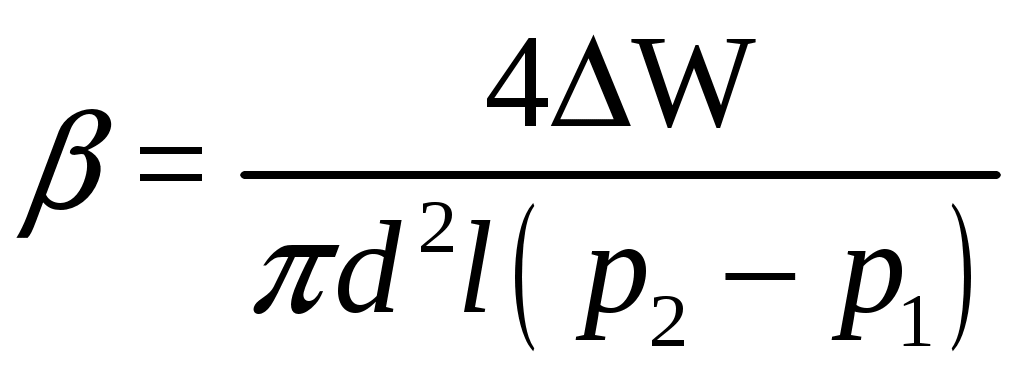 , ,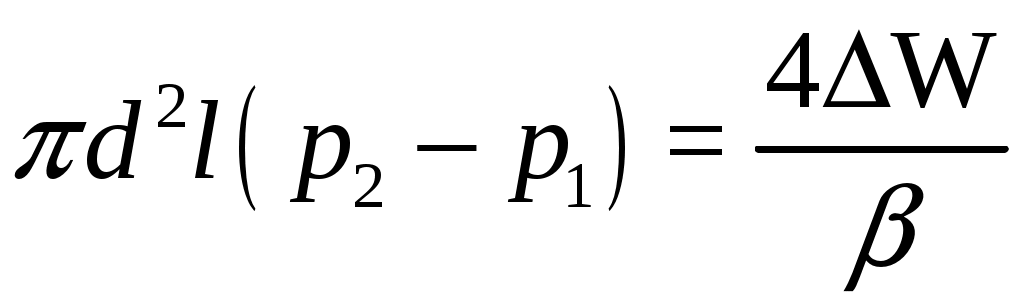 , ,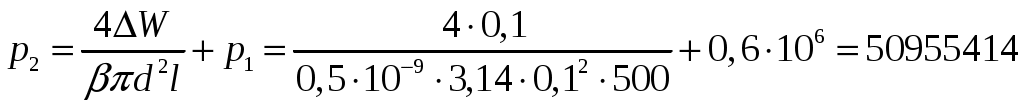 Па. Па.Задача 8. Определить результирующую силу гидростатического давления воды на сегментный затвор радиусом 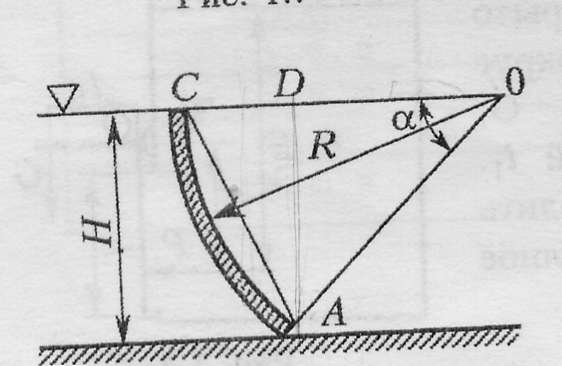 Решение Определяю горизонтальную составляющую силы гидростатического давления где Вертикальная составляющая силы давления определится по формуле: где Площадь ABCD равна площади сегмента ACB плюс площадь треугольника ACD. Равнодействующая сил давления определится по формуле Для определения координат центра давления Принимаем за начало координат точку О, тогда Подставляем найденное значение для Задача 13. Определить расход воды Q и скорость Решение Составляю уравнение Бернулли для сечений 1-1 и 2-2, принимая за плоскость сравнения ось трубы: Учитывая, что, полагая Предполагаем, что движение происходит в квадратичной зоне сопротивления, Определяю параметр Рейнольдса Значит, движение происходит в области гидравлически гладких труб Из уравнения неразрывности определяю Q. Задача 17. Определить эквивалентную длину Решение Потери напора по длине определяются по формуле Дарси-Вейсбаха 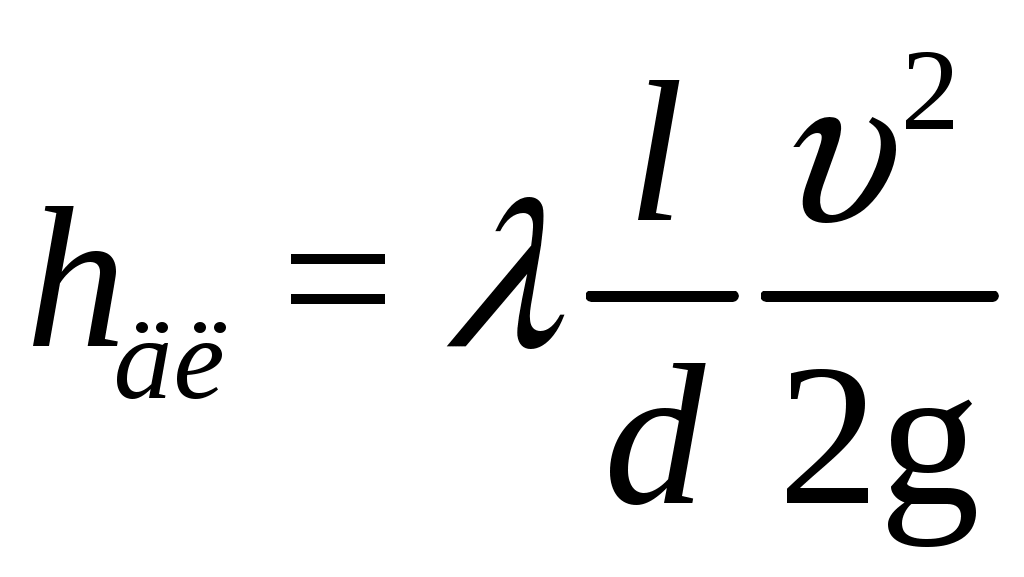 . .Местные потери напора определяются по формуле Борда-Карно 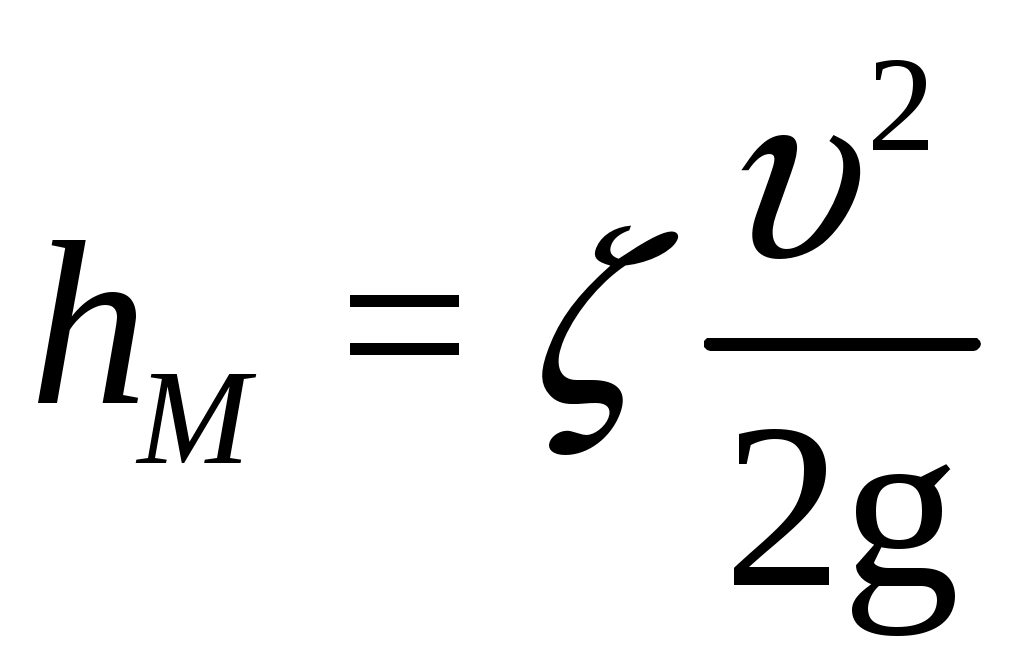 . .Заменяю местные потери напора эквивалентными потерями напора по длине 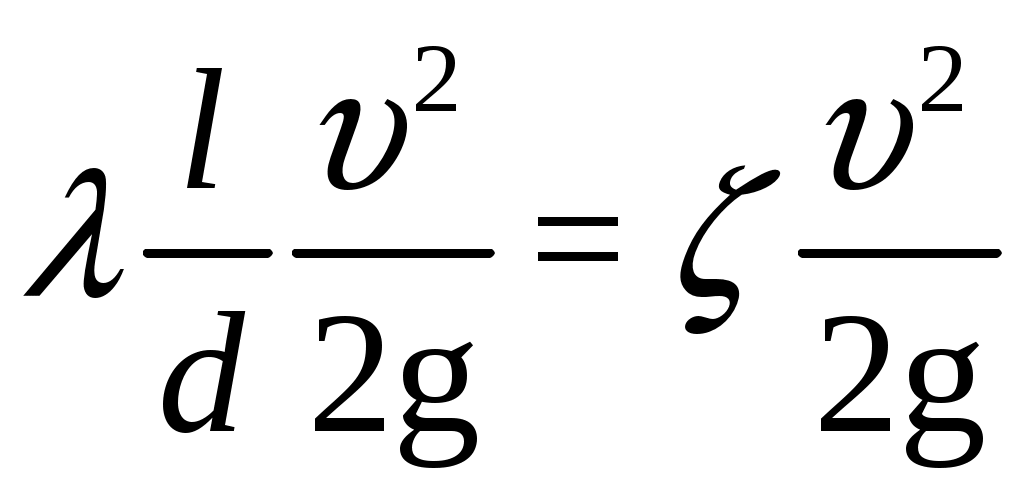 , ,Для определения 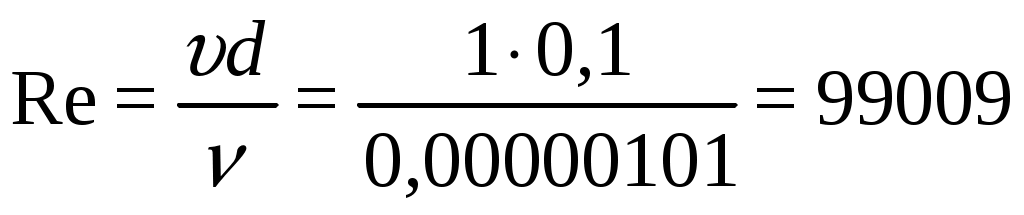 . .Таким образом, 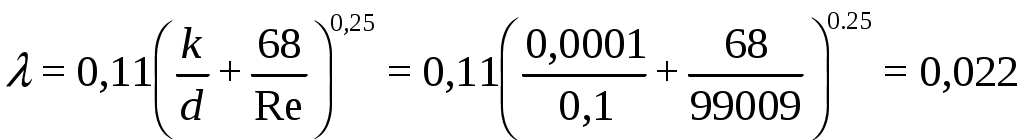 . .Таким образом, 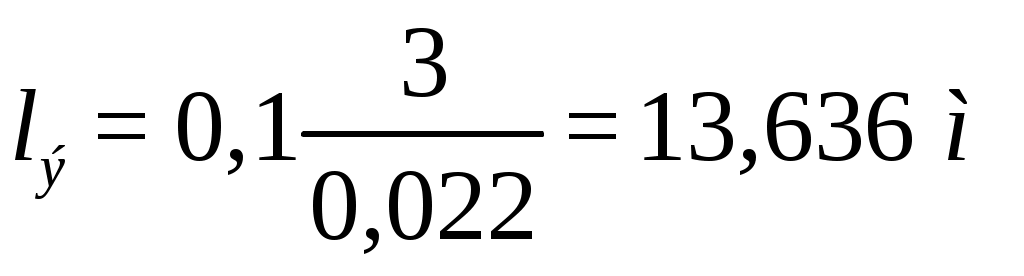 . .Задача 24. Определить диаметр сифона для пропуска воды из водоема А в водоем В, если разность уровней воды в водоемах 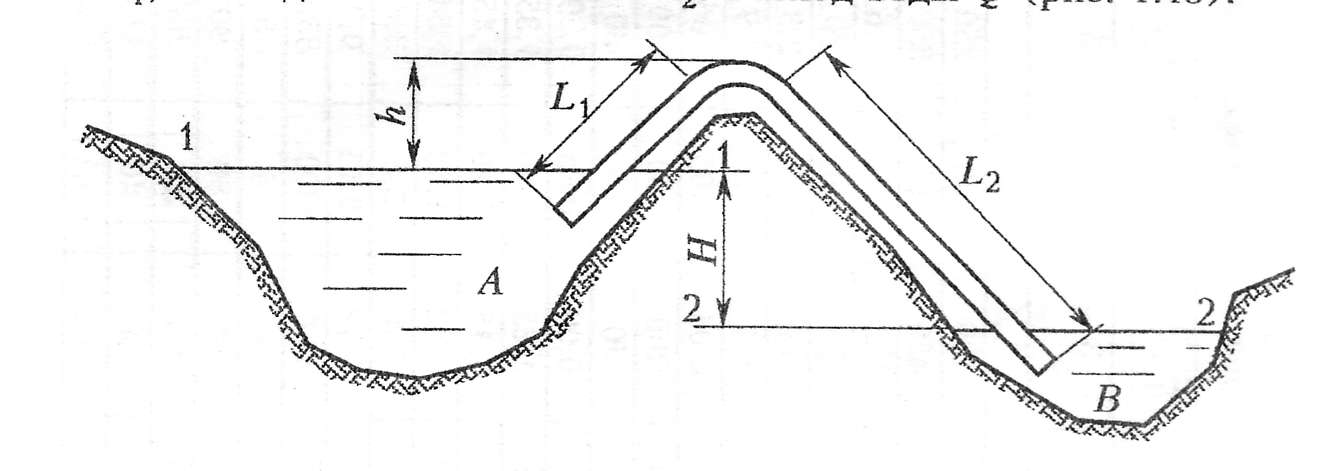 Решение Составляю уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 2-2. 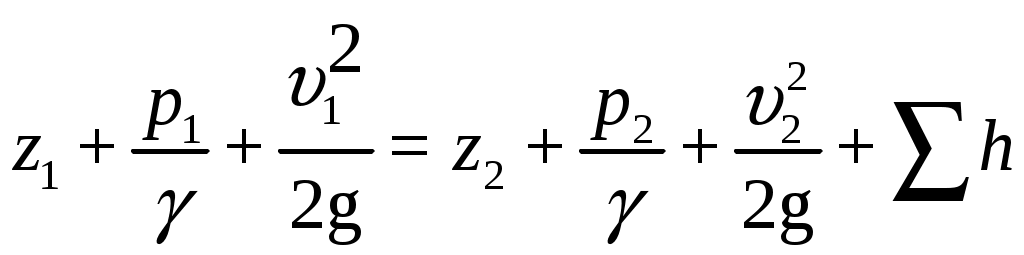 , ,Потери напора по длине определяю по формуле Дарси-Вейсбаха: 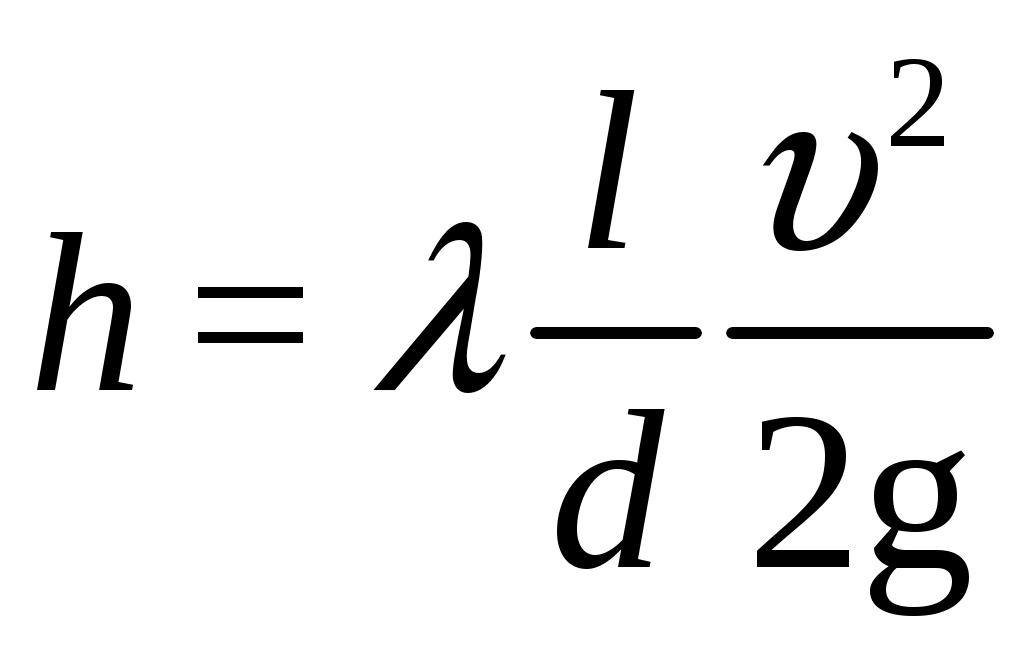 , ,где коэффициент гидравлического трения местные потери определяю по формуле Борда-Карно 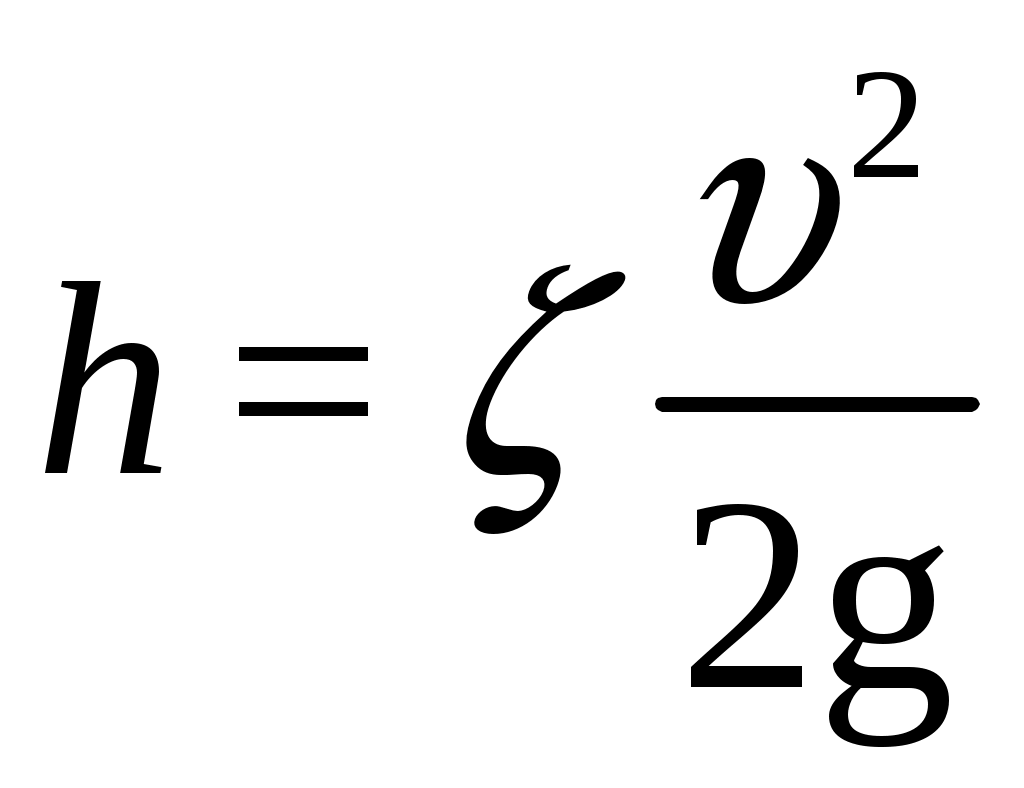 . .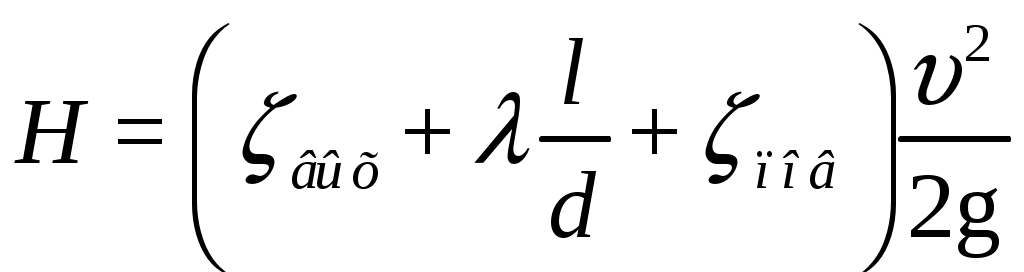 , ,Скорость выразим из уравнения неразрывности 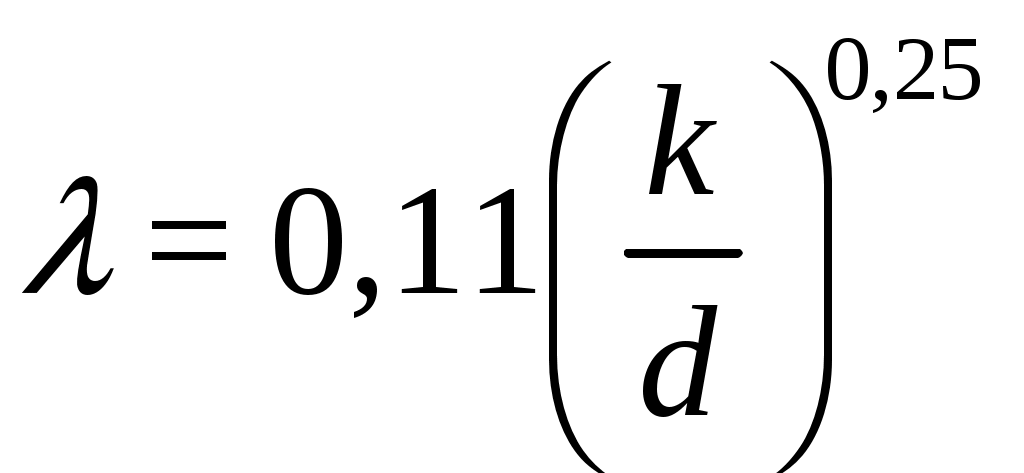 . .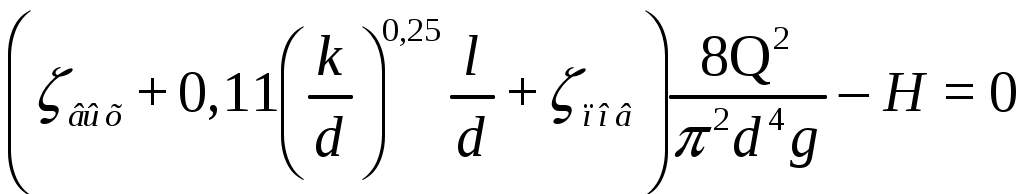 , ,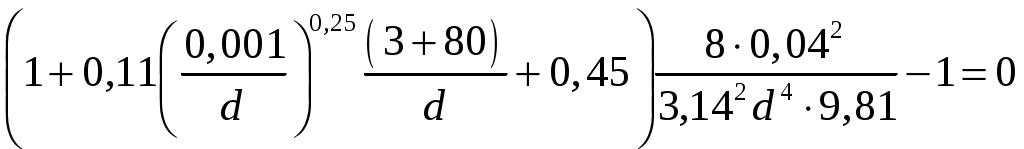 Полученное уравнение решается методом Ньютона, я же использую функцию «подбор параметра» в MS Excel. Проверяю режим движения 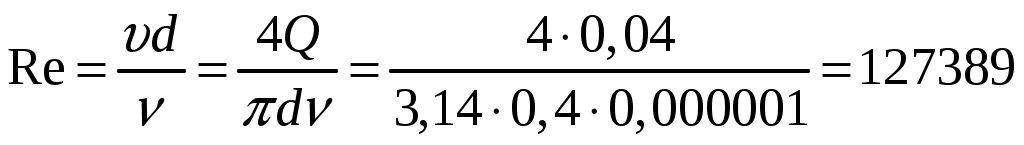 , ,Следовательно, как и предполагалось движение происходит в квадратичной области сопротивления. |
