Задачи про возраст. Задача про возраст и книги на полках
 Скачать 62.36 Kb.
|
|
Задача про возраст и книги на полках, решаемые арифметическими способами А.В. Шевкин, avshevkin@mail.ru Рассмотрим задачи, которые обычно решают при помощи уравнения, хотя более простым является арифметический способ решения. Отметим ещё одну общую черту приведённых ниже решений: они начинаются «с конца», с ситуации «стало» — после того, как прошло несколько лет, или после того, как несколько книг переставили с полки на полку. И последняя деталь, на которую стоит обратить внимание: «переставили с первой на вторую» и «переставили с одной на другую» — не одно и то же. 1 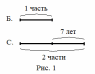 . Брату было 3 года, когда сестре исполнилось 10 лет, а сейчас сестра в 2 раза старше брата. Сколько лет брату сейчас?Решение.I способ. Пусть сейчас возраст брата составляет 1 часть, тогда возраст сестры составляет 2 такие же части (рис. 1), а разница в возрасте сестры и брата равна 10 – 3 = 7 (лет). Следовательно, на 2 – 1 = = 1 (часть) приходится 7 лет, т. е. брату сейчас 7 лет. II способ. Когда сестре было 10, она была старше брата в 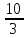 раза, прибавляя по 1, по 2, по 3, … к числителю и к знаменателю дроби, будем уменьшать первоначальную дробь, пока не получим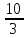 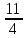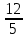2: > 2, 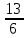 > 2,  > 2, 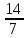 > 2,  = 2.Следовательно, сейчас брату 7 лет. Замечание. Эту задачу с помощью уравнения можно решить тоже двумя способами. III способ. Пусть x лет — возраст брата сейчас, тогда возраст сестры сейчас 2x лет, а разница в возрасте сестры и брата равна 10 – 3 = 7 (лет). Составим уравнение: 2x – x = 7. Уравнение имеет единственный корень x = 7, следовательно, сейчас брату 7 лет. IV способ. Пусть x лет тому назад брату было 3 года, а сестре 10 лет. Тогда сейчас брату (3 + x) лет, а сестре (10 + x) лет. Так как сестра в 2 раза старше брата, то составим уравнение: 10 + x = 2(3 + x). Уравнение имеет единственный корень x = 4, следовательно, сейчас брату 3 + 4 = 7 (лет). Ответ. 7 лет. 2. Саше было 6 лет, когда папе исполнилось 30 лет, а сейчас папа в 3 раза старше Саши. Сколько лет Саше сейчас? Эта задача похожа на предыдущую и первый способ её решения кажется более простым. Р 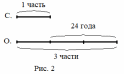 ешение.Пусть сейчас возраст Саши составляет 1 часть, тогда возраст папы составляет 3 такие же части (рис. 2).1) 30 – 6 = 24 (года) — разница в возрасте отца и Саши; 2) 3 – 1 = 2 (части) — приходится на 24 года; 3) 24 : 2 = 12 (лет) — приходится на 1 часть, т. е. Саше сейчас 12 лет. Ответ. 12 лет. 3. Даше было 5 лет, когда маме исполнилось 26 лет, а сейчас мама в 4 раза старше Даши. Сколько лет маме сейчас? Ответ. 28 лет. 4. В двух карманах было 120 руб. Когда из первого кармана переложили во второй 15 руб., то во втором кармане стало в 3 раза больше денег, чем в первом. Сколько денег было в первом кармане первоначально? Р 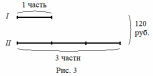 ешение.Пусть после перекладывания сумма денег во I-м кармане составляет 1 часть, тогда сумма денег в II-м кармане составляет 3 такие же части.1) 1 + 3 = 4 (части) — приходится на 120 руб.; 2) 120 : 4 = 30 (руб.) — приходится на 1 часть, столько стало в I-м кармане. 3) 30 + 15 = 45 (руб.) — было первоначально в I-м кармане. Ответ. 45 руб. 5. В двух карманах было 160 руб. Когда из второго кармана переложили в первый 12 руб., то во втором кармане стало в 3 раза больше денег, чем в первом. Сколько денег было в первом кармане первоначально? Р 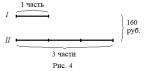 ешение.Пусть после перекладывания сумма денег во I-м кармане составляет 1 часть, тогда сумма денег в II-м кармане составляет 3 такие же части.1) 1 + 3 = 4 (части) — приходится на 120 руб.; 2) 160 : 4 = 40 (руб.) — приходится на 1 часть, столько стало в I-м кармане. 3) 40 – 12 = 28 (руб.) — было первоначально в I-м кармане. Ответ. 28 руб. 6. На двух полках стояло 60 книг. Когда с одной полки переставили на другую 4 книги, то на первой полке стало в 2 раза больше книг, чем на второй. Сколько книг было на первой полке первоначально? Решение.Пусть после перекладывания четырёх книг число книг на II-й полке составляет 1 часть, а на I-й полке — 2 такие же части. 1 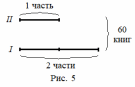 ) 2 + 1 = 3 (части) — приходится на 60 книг;2) 60 : 3 = 20 (книг) — приходится на 1 часть, столько книг стало на II-й полке; 3) 20 ∙ 2 = 40 (книг) — стало на I-й полке. В задаче не сказано, с какой полки переставили 4 книги, рассмотрим два случая. Пусть книги снимали с I-й полки. 4) 40 + 4 = 44 (книги) — было на I-й полке первоначально. Пусть книги снимали с II-й полки. 5) 40 – 4 = 36 (книг) — было на I-й полке первоначально. Ответ. 44 или 36 книг. 7. На двух полках стояло 80 книг. Когда с одной полки переставили на другую 6 книг, то на одной из этих полок стало в 3 раза больше книг, чем на другой. Сколько книг было на каждой полке первоначально? Решение. Здесь не известно, с какой полки переставили книги на другую — с первой или второй. Пусть число книг на одной полке составляет 1 часть, на другой — 3 такие же части. 1) 3 + 1 = 4 (части) — приходится на 80 книг; 2) 80 : 4 = 20 (книг) — приходится на 1 часть, столько книг стало на одной из полок; 3) 20 ∙ 3 = 60 (книг) — стало на другой полке. Рассмотрим два случая. Пусть книги снимали с той полки, где их стало меньше (назовём её I-й полкой). 4) 20 + 6 = 26 (книг) — было на I-й полке первоначально; 5) 60 – 6 = 54 (книг) — было на II-й полке первоначально; Пусть книги снимали с той полки, где их стало больше (назовём её II-й полкой). 6) 20 – 6 = 14 (книг) — было на I-й полке первоначально; 7) 60 + 6 = 66 (книг) — было на II-й полке первоначально; Ответ. 26 и 54 книг или 14 и 66 книг. |