РАСЧЁТ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЛИНЕЙНЫХ САУ. Задача расчёт динамических характеристик линейных сау
 Скачать 249.5 Kb.
|
|
ЗАДАЧА 1. РАСЧЁТ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЛИНЕЙНЫХ САУ О  пределить весовую функцию g(t) и переходную функцию h(t) линейной САУ, состоящей из последовательно соединенных апериодического и идеального интегрирующего звеньев по заданным параметрам её передаточной функции: где р-оператор Лапласа. Составить таблицу расчётных значений искомых временных характеристик и построить их графики с шагом дискретизации, равным 0,5Т, для временного интервала: t=0-5T. Масштаб по оси ординат выбрать самостоятельно, исходя из того, что высота графика должна быть не менее 8-10 см. Исходные данные: Номер варианта - 01; К = 5; Т = 1 сек Решение: И  зображение весовой функции L[g(t)] - это её передаточная функция: Для отыскания оригинала весовой функции g(t)=L-1[W(p)] разложим W(p) на элементарные дроби, соответствующие передаточным функциям простых звеньев и воспользовавшись методом неопределённых коэффициентов найдем неизвестные коэффициенты:  (1) П 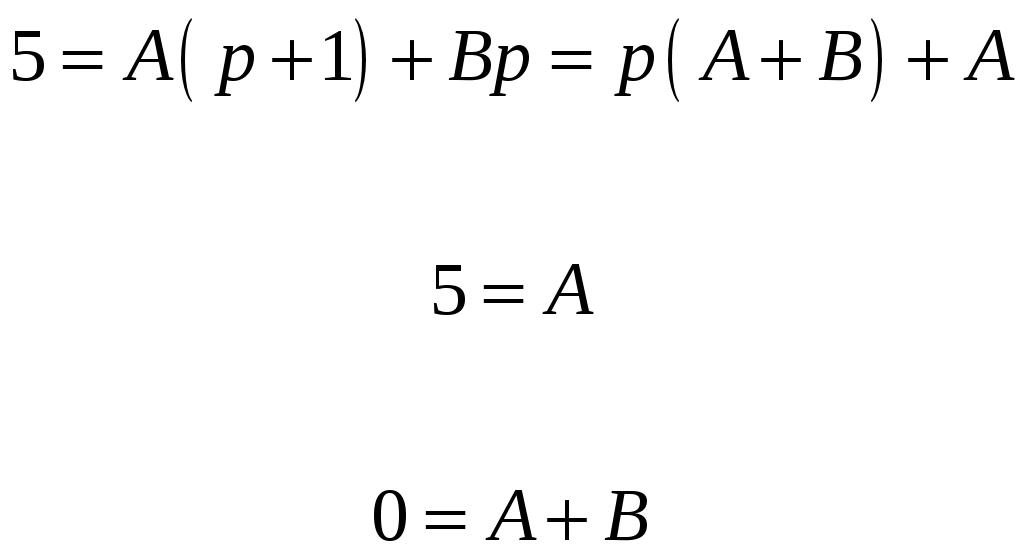 осле приведения правой части выражения (1) к общему знаменателю приравниваем коэффициенты числителей правой и левой частей при одинаковых степенях переменной р, получим:(2) Решаем систему последних двух уравнений и находим: А=5; В=-5 П  одставляя численные значения коэффициентов А и В в уравнение (1) получим:(3) Переход от изображений к их оригиналам, сделаем с помощью таблиц изображений, получим: оригинал функции 1/р равен: L-1[1/p]=1; оригинал функции 1/(р+1) равен: L-1[1/p]=e-t; З  аменив в правой части уравнения (3) изображения функций на их оригиналы, получим искомое выражение для весовой функции:(4) Задавая различные значения t, заполним таблицу 1 и построим график g(t). Таблица 1
График весовой функции g(t) приведён на рисунке 1. 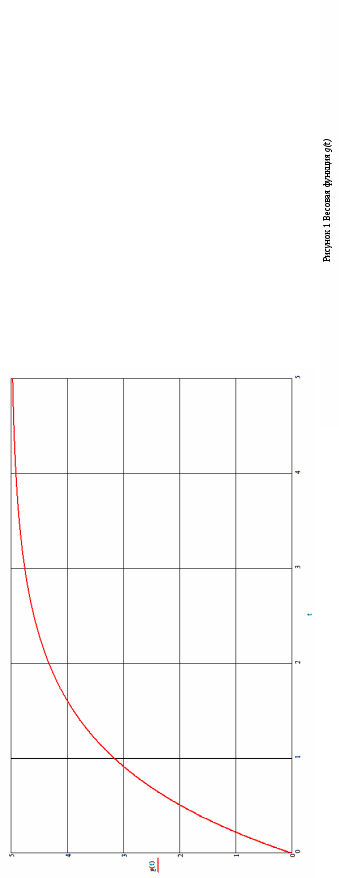 По известной весовой функции g(t) можно найти переходную функцию h(t), принимая во внимание, что  Изображение функции h(t) можно получить умножением исходной передаточной функции W(p) на передаточную функцию 1/р идеального интегрирующего звена  (5) Далее, аналогично вышеизложенному, применяя метод неопределённых коэффициентов, разложим изображение переходной функции h(t) на более простые изображения функций. 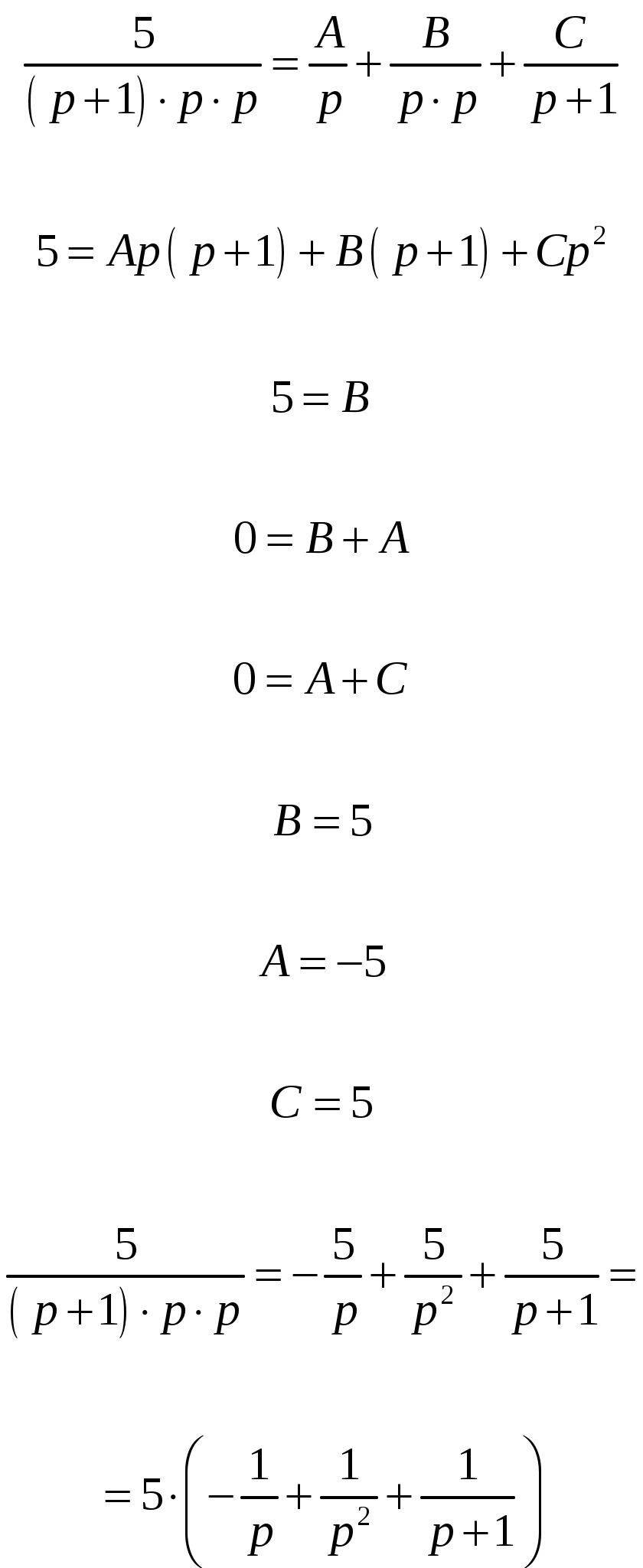 Воспользовавшись таблицами изображений, получим: оригинал функции 1/р равен: L-1[1/p]=1; оригинал функции 1/р2 равен: L-1[1/ р2]=t; оригинал функции 1/(р+1) равен: L-1[1/p]=e-t; Тогда переходная функция h(t) равна:  Задавая различные значения t, заполним таблицу 2 и построим график h(t). Таблица 2
График переходной функции h(t) приведён на рисунке 2. 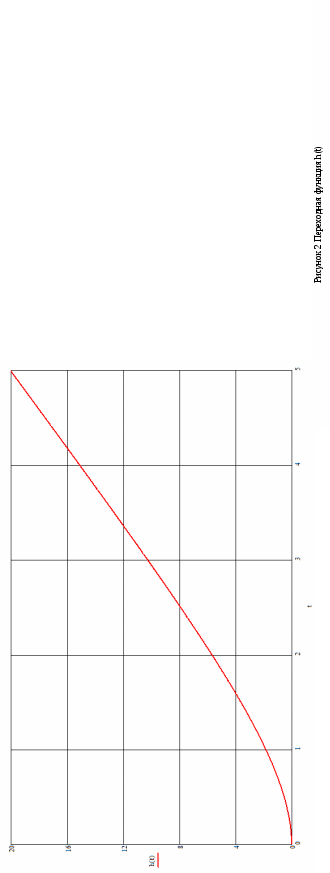 ЗАДАЧА 2. РАСЧЁТ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЛИНЕЙНЫХ САУ Определить круговую частоту ω, с которой устройство САУ, состоящее из последовательно включённых двух апериодических и одного идеального интегрирующего звеньев, даёт заданный сдвиг по фазе между выходным и входным сигналами. При этом следует определить амплитуду выходного сигнала Y на данной частоте, если известна амплитуда входного сигнала Х. Передаточная функция:  Исходные данные: К = 10; Т1 = 0,05сек; Т2 = 0,5сек; Х=7; φ=-1700 Решение: По передаточной функции W(p), представленной в операторной форме, найдём выражение для частотной передаточной функции W(jω) путём замены в передаточной функции оператора Лапласа р на комплексную переменную jω.   где модуль частотной передаточной функции, представляющий собой амплитудно-частотную характеристику (АЧХ) системы САУ.  аргумент частотной передаточной функции, представляющий собой фазо-частотную характеристику (ФЧХ) системы САУ. Задавая различные значения ω, заполним таблицу 3 и построим график φ(ω). Таблица 3
График фазо-частотной характеристики φ(ω) приведён на рисунке 3. 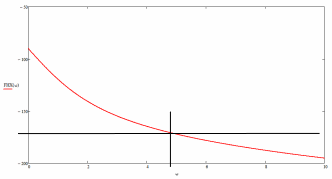 Рисунок 3 Фазо-частотная характеристика φ(ω) Проводим горизонтальную прямую через значение φ(ω) = -1700 и вертикальную прямую через точку пересечения горизонтальной прямой с ФЧХ, по оси частот ω определяем круговую частоту ωН, на которой обеспечивается заданный по условию сдвиг фазы. В нашей задаче: ωН = 4,7. П 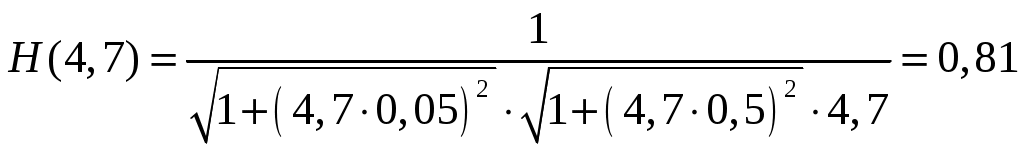 одставляем найденное значение в выражение для АЧХ находим его значение:Амплитуда выходного сигнала равна:  ЗАДАЧА 3. ПОСТРОЕНИЕ ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК И ГОДОГРАФА АФЧХ 1. Построить асимптотическую логарифмическую амплитудно-частотную характеристику (ЛАЧХ) и логарифмическую фазо-частотную характеристику (ЛФЧХ) для линейной системы САУ, состоящей из четырёх последовательно включённых звеньев: -одного реального дифференцирующего звена с передаточной функцией W1(p) = K1·(T1 p+1); -двух апериодических звеньев первого порядка с передаточными функциями W2(p) = K2/(T2 p+1) и W3(p) = K3/(T3 p+1); -одного идеального интегрирующего звена с передаточной функцией W4(p) = K4/p. Передаточная функция заданной линейной САУ 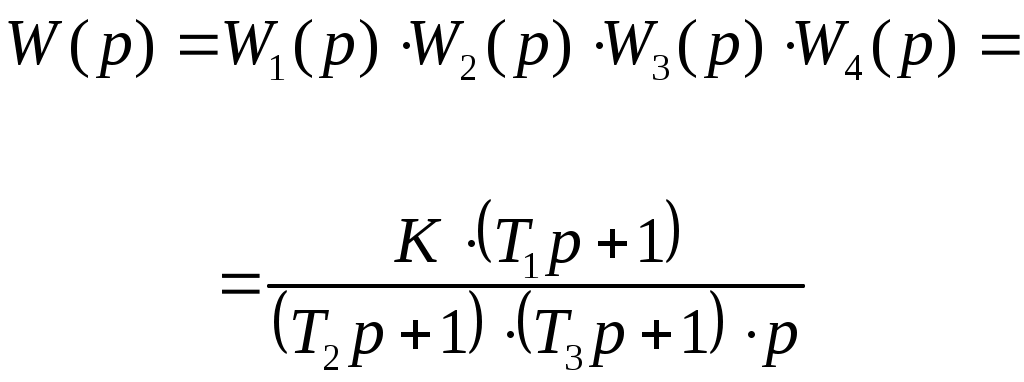 где К=К1·К2·К3·К4 2. Построить годограф АФЧХ W(jω) заданной САУ. Исходные данные: номер варианта - 10; К = 100; Т1 = 0,125сек; Т2 = 2сек; Т3 = 0,5сек; Решение: Найдём выражение для логарифмической АЧХ и ФЧХ, для чего сначала определим АФЧХ системы по её передаточной функции W(р), заменяя в ней оператор Лапласа р на комплексную переменную jω. 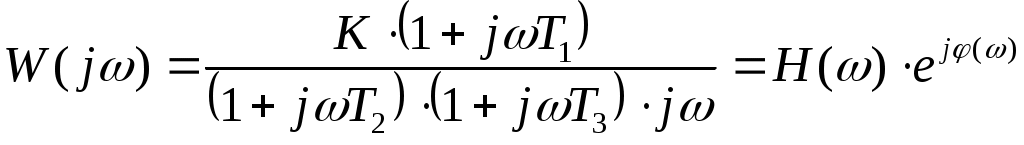 г 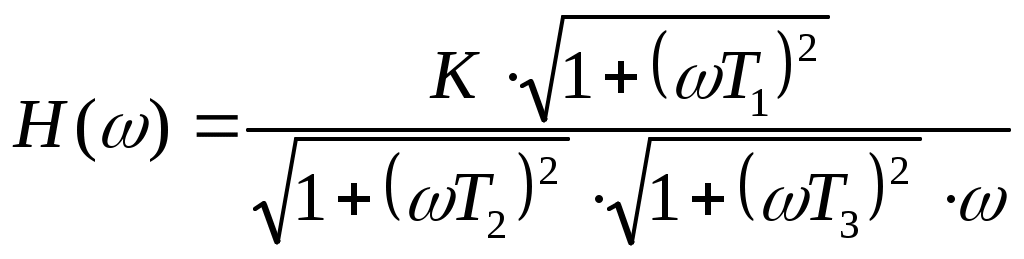 деамплитудно-частотная характеристика (АЧХ) системы САУ.  аргумент частотной передаточной функции, представляющий собой фазо-частотную характеристику (ФЧХ) системы САУ. По известной АЧХ определим выражение для ЛАЧХ L(ω) 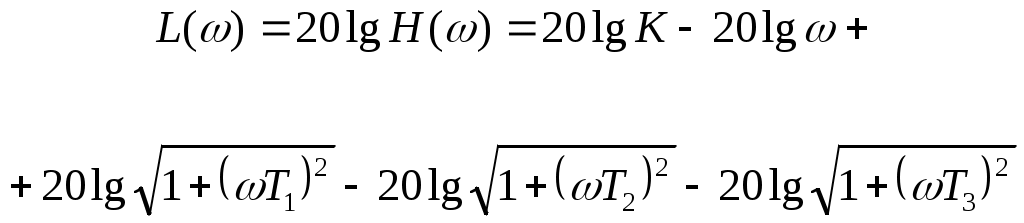 , дБ Асимптотическую ЛАЧХ строим путем замены непрерывной кривой ЛАЧХ несколькими прямыми отрезками, которые сопрягаются между собой в точках, соответствующих круговым частотам ωС (сопрягающим частотам), численно равным обратной величине от постоянных времени, входящих в выражение для ЛАЧХ. У нас три сопрягающих частоты: ωС1 = 1/Т1 = 1/0,125 = 8 рад/сек; ωС2 = 1/Т2 = 1/2 = 0,5 рад/сек; ωС3 = 1/Т3 = 1/0,5 = 2 рад/сек; Отмечаем их на оси частот. На оси ординат, которую проводим через частотную отметку ω = 0,1 рад/сек, находим точку 20·lgK - 20·lgω и от неё вправо проводим прямую линию с наклоном -20дБ на декаду до пересечения с вертикальной линией соответствующей второй сопрягающей частоте ωС2 = 0,5 рад/сек. На отрезке оси частот 0,1 ≤ ω ≤ ωС2асимптотическая ЛАЧХ описывается выражением L(ω) = 20·lgK - 20·lg ω и представляет собой отрезок ранее проведённой прямой, ординаты концов этой прямой равны: L(0,1) = 20·lgK - 20·lg 0,1 = 60 дБ L(0,5) = 20·lgK - 20·lg 0,5 = 46 дБ Вторая сопрягающая частота ωС2 принадлежит апериодическому звену, поэтому после этой частоты асимптотическая ЛАЧХ на отрезке оси частот ωС2 ≤ ω ≤ ωС1 описывается выражением: L(ω) = 20·lgK - 20·lg ω - 20·lg (ω Т2) и следовательно её наклон увеличивается на -20дБ/дек и становится равным -40дБ/дек. Ордината в точке ωС3 = 2 рад/сек равна: L(2) = 20·lgK - 20·lg 2 - 20·lg (2·2) = 22 дБ Третья сопрягающая частота ωС3 принадлежит апериодическому звену, поэтому после этой частоты асимптотическая ЛАЧХ на отрезке оси частот ωС1 ≤ ω ≤ ωС3 описывается выражением: L(ω) = 20·lgK - 20·lg ω - 20·lg (ω Т2) - 20·lg (ω Т3) и следовательно её наклон увеличивается на -20дБ/дек и становится равным -60дБ/дек. Ордината в точке ωС1 = 8 рад/сек равна: L(8) = 20·lgK - 20·lg 8 - 20·lg (8·2) - 20·lg (8·0,5) = -14 дБ Первая сопрягающая частота ωС1 принадлежит дифференцирующему звену, поэтому после этой частоты асимптотическая ЛАЧХ на отрезке оси частот ωС3 ≤ ω описывается выражением: L(ω) = 20·lgK - 20·lg ω - 20·lg (ω Т2) - 20·lg (ω Т3) + 20·lg (ω Т1) и следовательно её наклон уменьшается на -20дБ/дек и становится равным -40дБ/дек. Ордината в точке ω = 10 рад/сек равна: L(10) = 20·lg K - 20·lg 10 - 20·lg (10·2) - 20·lg (10·0,5) + 20·lg (10·0,125) = = -18 дБ На рисунке 5 приведён график логарифмической асимптотической ЛАЧХ, построенный в соответствии с вышеприведённым алгоритмом. Д ля построения логарифмической ФЧХ воспользуемся выражением:Задавая различные значения ω, заполним соответствующий столбец таблицы 4 и построим график φ(ω). График логарифмической фазо-частотной характеристики φ(ω) приведён на рисунке 5. Для построения годографа АФЧХ вычислим модуль Н(ω) частотной передаточной функции и его проекции на мнимую ось M(ω) и действительную ось N(ω) и результаты вычислений занесём в таблицу 4: 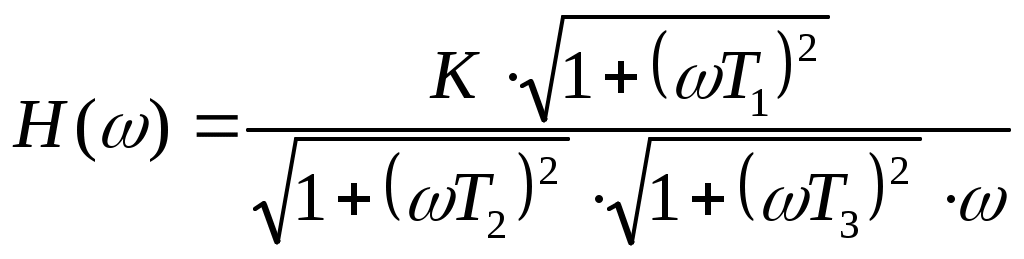M(ω) = Н(ω)·sin [φ(ω)] N(ω) = Н(ω)·cos [φ(ω)] Таблица 4
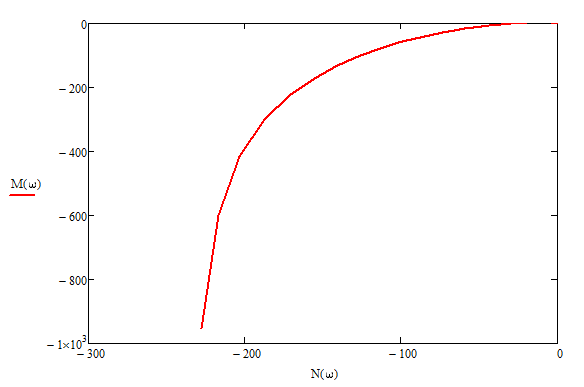 ω=10 ω=0,1 Рисунок 4 Годограф АФЧХ 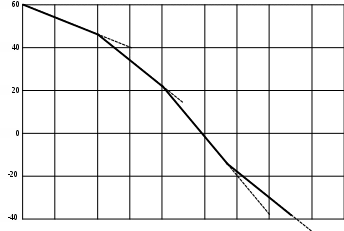  Рисунок 4 Логарифмические асимптотическая амплитудно-частотная и фазо-частотная характеристики Литература 1. Теория автоматического управления. Второе изд./ Под ред. акад. А. А. Воронова.- М.: Высшая школа, 1986, ч.I и II. 2. Я.З. Цыпкин. Основы теории автоматических систем. - М.: Наука, 1977. |