Решения 7 класс 2020(1). Задача решена полностью (при этом способ решения, предложенный учеником, может кардинально отличаться от авторского)
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
|
При проверке олимпиадной работы руководствуйтесь критериями оценивания, приведёнными ниже после решения каждой из задач. Если какие-то пункты критериев в явном виде отсутствуют, но в дальнейшем решении используются, то они должны быть засчитаны. При этом проверяющий имеет право ставить неполный балл за действие, обозначенное в критериях, если оно выполнено учащимся частично. Каждая задача (независимо от уровня сложности) оценивается из 10 баллов. Предложенные учениками решения задач могут быть правильными, даже если эти решения кардинально отличаются от авторских! В этом случае рекомендуется придерживаться следующих критериев оценивания: 0 баллов – если ученик не приступал к решению задачи или приступил, но никаких разумных соображений не привёл; 1 - 5 баллов – если ученик написал разумные соображения, уравнения и рисунки, но полную систему уравнений для решения задачи составить не смог; 6 - 8 баллов – ученик понял физику решения, составил полную систему уравнений, необходимую для решения задачи, но довести решение системы до конца не смог; 9 баллов – ученик решил правильно задачу в общем виде (получил буквенный ответ), но сделал математические ошибки в окончательных вычислениях; 10 баллов – задача решена полностью (при этом способ решения, предложенный учеником, может кардинально отличаться от авторского). 7 класс Задача 1. Из А в Б. Автомобиль двигался из пункта А в пункт Б. На первом участке пути его скорость была выше средней, на втором – равнялась средней, а на третьем – в 2 раза меньше средней. Скорости движения на каждом участке постоянны. Оказалось, что время прохождения третьего участка в 2 раза больше, чем первого. Во сколько раз скорость автомобиля на первом участке больше, чем на третьем? Возможное решение. По определению средней скорости  (3 балла) (3 балла) (3 балла) (3 балла)откуда  (2 балла) (2 балла)и 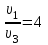 (2 балла) (2 балла)Задача 2. Фотоохота. Однажды зоолог Бот фотографировал червячка. Но так получилось, что на двух снимках, сделанных с интервалом 30 с, червячок попал в кадр лишь частично. Определите длину L червячка, если за 2 минуты он уполз на 80 см. 1 дюйм равен 2,54 см.  Возможное решение. Цена деления линейки 0,25 дюйма. Значит координата головы червяка на 1 рисунке xг0 = 23,5 дюйма ≈ 59,7 см. (2 балла) Если за 2 минуты червяк уполз на 80 см, то за время между кадрами он сместился на 20 см. (2 балла) Новая координата головы червячка xг1 = xг0 - 20 см = 39,7 см. (2 балла) Координата хвоста в это время xх1 = 20,25 дюйма ≈ 51,4 см. (2 балла) Длина червячка L = xх1 - xг1 = 11,7 см. (4,6 дюйма) (2 балла) Так как задача подразумевает значительное число округлений, численный ответ следует оценивать через попадания в ворота: L € [11,5 .. 12,0] см или L € [4,53 .. 4,72] дюйма - 2 балла. L € [11,0 .. 12,5] см или L € [4,33 .. 4,92] дюйма - 1 балл. Задача 3. Жесть, а не коробочка. В распоряжении экспериментатора Глюка оказался тонкий квадратный лист жести массой m0 = 512 г с длиной стороны L = 80 см. Глюк вырезал из него несколько квадратных заготовок с длиной стороны a = 10 см и сделал из них полые кубики, из которых затем составил один большой куб с длиной стороны 2a. Определите: какое максимальное количество маленьких кубиков можно изготовить? массу Mбольшого куба. Возможное решение. Из данного листа жести можно вырезать 8 рядов по 8 квадратов заданного размера. Всего 64 заготовки. (1 балл) Масса каждой заготовки  . (1 балл) . (1 балл)Кубик будет состоять из 6 квадратных граней. (2 балла) Масса кубика  . (1 балл) . (1 балл)Значит, всего можно будет изготовить 10 кубиков (4 квадрата останутся). (2 балла) Куб будет состоять из 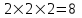 кубиков. (2 балла) кубиков. (2 балла)Масса большого куба 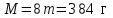 . (1 балл) . (1 балл)Задача 4. Однажды в аквариуме. В прямоугольный аквариум с вертикальными стенками частично заполненный водой, поставили цилиндр высотой H = 60 см. В результате уровень воды поднялся до середины цилиндра. Затем в аквариум опустили другой такой же цилиндр, при этом уровень воды поднялся до высоты H. Определите высоту h уровня воды до погружения цилиндров. Вода из аквариума не вытекает. Цилиндры не плавают. Возможное решение. Объём воды в аквариуме не изменяется. До погружения цилиндров его можно рассчитать по формуле 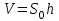 , где S0 - площадь дна аквариума. (2 балла) , где S0 - площадь дна аквариума. (2 балла)Из первой ситуации следует, что объём воды можно записать так:  , где S1 - площадь цилиндра. (2 балла) , где S1 - площадь цилиндра. (2 балла)После погружения 2-го цилиндра:  . (2 балла) . (2 балла)Приравняв (2) и (3) получим соотношение площадей  . (2 балла) . (2 балла)Приравняв (1) и (3) или (2), и подставив (4) получим выражение для h: 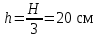 (2 балла) (2 балла) |
