Главная страница
Навигация по странице:

  • ИТОГОВОЕ ПРАКТИЧЕСКОЕ ЗАДАНИЕ по дисциплине « Математическое моделирование

  • ФИО студента Фролов Михаил Александрвич Направление подготовки

  • Группа ПМИ-б-01-д-2017 Москва 2021

    		•

    Ипз. ипз - Copy. Задача с решением


    Скачать 43.77 Kb.
    НазваниеЗадача с решением
    Дата14.04.2021
    Размер43.77 Kb.
    Формат файлаdocx
    Имя файлаипз - Copy.docx
    ТипЗадача
    #194883
    Российский государственный социальный университет



    ИТОГОВОЕ ПРАКТИЧЕСКОЕ ЗАДАНИЕ

    по дисциплине «Математическое моделирование»
    __________Динамическое программирование__________

    (тема практического задания)

    ФИО студента
    Фролов Михаил Александрвич

    Направление подготовки
    Прикладная математика и информатика

    Группа
    ПМИ-б-01-д-2017


    Москва 2021

    Задача с решением.



    Имеются четыре предприятия, между которыми необходимо распределить 100 тыс. усл.ед. средств. Значения прироста выпуска продукции на предприятиях в зависимости от выделенных средств X представлены в таблице. Составить оптимальный план распределения средств, позволяющий максимизировать общий прирост выпуска продукции.

    Таблица 1

    X
    g1
    g2
    g3
    g4

    0
    0
    0
    0
    0

    20
    14
    17
    22
    20

    40
    26
    20
    21
    33

    60
    35
    32
    37
    46

    80
    52
    61
    67
    30

    100
    61
    72
    58
    42

    Решение

    Этап I. Условная оптимизация.

    Шаг 1. k = 4. Предполагаем, что все средства 100 ден.ед. переданы на инвестирование четвертого предприятия. В этом случае максимальная прибыль составит F4(C4)= 46, данные представлены в таблице 2

    Таблица 2.

    C4
    x4
    F4(C4)
    X*

    0
    20
    40
    60
    80
    100

    0
    0
    -
    -
    -
    -
    -
    0
    0

    20
    -
    20
    -
    -
    -
    -
    20
    20

    40
    -
    -
    33
    -
    -
    -
    33
    40

    60
    -
    -
    -
    46
    -
    -
    46
    60

    80
    -
    -
    -
    -
    30
    -
    30
    80

    100
    -
    -
    -
    -
    -
    42
    42
    100

    Шаг 2. k = 3. Определяем оптимальную стратегию инвестирования в третье и четвертое предприятия. При этом рекуррентное соотношение Беллмана будет иметь вид:

    .

    На его основании рассчитываются данные таблицы 3

    Таблица 3.

    C3
    X3
    F3(C3)
    X*

    0
    20
    40
    60
    80
    100

    0
    0+0
    -
    -
    -
    -
    -
    0
    0

    20
    0+20
    22+0
    -
    -
    -
    -
    22
    20

    40
    0+33
    22+20
    21+0
    -
    -
    -
    42
    20

    60
    0+46
    22+33
    21+20
    37+0
    -
    -
    55
    20

    80
    0+30
    22+46
    21+33
    37+20
    67+0
    -
    68
    20

    100
    0+42
    22+30
    21+46
    37+33
    67+20
    58+0
    87
    20

    Шаг 3. k = 2. Определяем оптимальную стратегию инвестирования во второе и третье предприятия. При этом рекуррентное соотношение Беллмана будет иметь вид:

    .

    На его основании рассчитываются данные таблицы 3.

    Таблица 3.

    C2
    X2
    F2(C2)
    X*

    0
    20
    40
    60
    80
    100

    0
    0+0
    -
    -
    -
    -
    -
    0
    0

    20
    0+22
    17+0
    -
    -
    -
    -
    22
    0

    40
    0+42
    17+22
    20+0
    -
    -
    -
    42
    0

    60
    0+55
    17+42
    20+22
    32+0
    -
    -
    59
    20

    80
    0+68
    17+55
    20+42
    32+22
    61+0
    -
    72
    20

    100
    0+87
    17+68
    20+55
    32+42
    61+22
    72+0
    87
    0

    Шаг 4. k = 1. Определяем оптимальную стратегию инвестирования в первое и остальные предприятия. При этом рекуррентное соотношение Беллмана будет иметь вид:

    .

    На его основе находятся данные таблицы 4.

    Таблица 4.

    C1
    X1
    F1(C1)
    X*

    0
    20
    40
    60
    80
    100

    0
    0+0
    -
    -
    -
    -
    -
    0
    0

    20
    0+48
    14+0
    -
    -
    -
    -
    22
    0

    40
    0+93
    14+48
    26+0
    -
    -
    -
    42
    0

    60
    0+135
    14+93
    26+48
    35+0
    -
    -
    59
    0

    80
    0+149
    14+135
    26+93
    35+48
    52+0
    -
    72
    0

    100
    0+160
    14+149
    26+135
    35+93
    52+48
    61+0
    87
    0

    По данным последней таблицы максимальных доход с четырех предприятий составил 87 д.ед. При этом первое и второе предприятия не принесут никакого дохода, в них нецелесообразно вкладывать инвестиции. В 3-е предприятие нужно вложить 80 д.ед. В 4-е предприятие нужно вложить 20 д.ед. В итоге останется 20-Получается, что оптимальный план Х*(0;0;80;20)
    Задача с ответом.

    Транспортная сеть состоит из 12 (m=12) узлов (городах), некоторые из которых соединены магистралями. Стоимость проезда по каждой из таких магистралей известна и отмечена на схеме (рис. 1).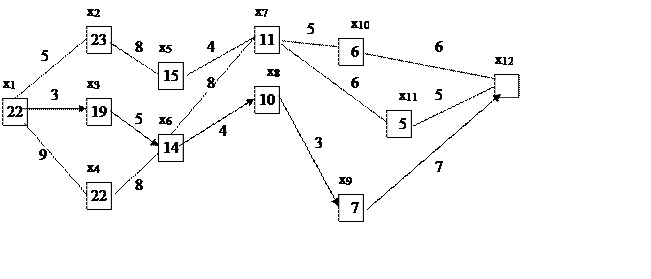


    Требуется найти оптимальный маршрут из 1-го пункта в 12-й. Движение только слева направо.

    Ответ: Х1-Х3-Х6-Х8-Х9-Х12

    Вопросы


    В процессе динамического программирования раньше всех планируется
    первый шаг
    последний шаг +
    как сказано в условии задачи
    предпоследний шаг

    В задачах динамического программирования шаговое управление должно выбираться
    с учетом последствий в будущем +
    с учетом предшествующих шагов
    и то, и другое
    наилучшим для данного шага
    лучше, чем предыдущее

    Задача о загрузке рюкзака является задачей …. Программирования
    нелинейного
    параметрического
    динамического +
    линейного
    целочисленного

    В задачах теории игр говорят, что игра имеет седловую точку, если
    нижняя цена игры меньше верхней
    нижняя цена игры равна верхней +
    нижняя цена игры больше верхней
    нижняя цена игры не больше верхней
    нижняя цена игры не меньше верхней

    написать администратору сайта