эконометрика. ммм вар 21. Задача состоит в нахождении такой допустимой производственной программы
 Скачать 306 Kb.
|
Содержание 1. Ситуационная (практическая) часть…………………………………………………3 2. Тестовая часть………………………………………………………………………..11 Список литературы……………………………………………………………………..13 1. Ситуационная (практическая) часть Предоставить подробное решение задачи 1 и задачи 4 с необходимыми чертежами. Задача 1. 1. Построить математическую модель оптимизации выпуска продукции и записать ее в форме задачи линейного программированияВведем перемнные: Пусть х1 – месячный объем выпуска продукции А; х2 – месячный объем выпуска продукции В. Используя данные таблицы, определим затраты каждого вида ресурса для выпуска производственной программы Х*=(х1, х2): Расход сырья: 3х1+х2 189; Загрузка оборудования: х1+5х2 315; Трудозатраты: 7х1+х2 615; Задача состоит в нахождении такой допустимой производственной программы Х=(х1, х2), которая обеспечивает получение наибольшего дохода: Z=196х1+364х2 max; Построенная математическая модель задачи представляет собой задачу линейного программирования, так как ограничения заданы в виде линейных неравенств, а оптимизируемый показатель (доход) выражается с помощью линейной функции. Таким образом, математическая модель данной задачи выглядит следующим образом: 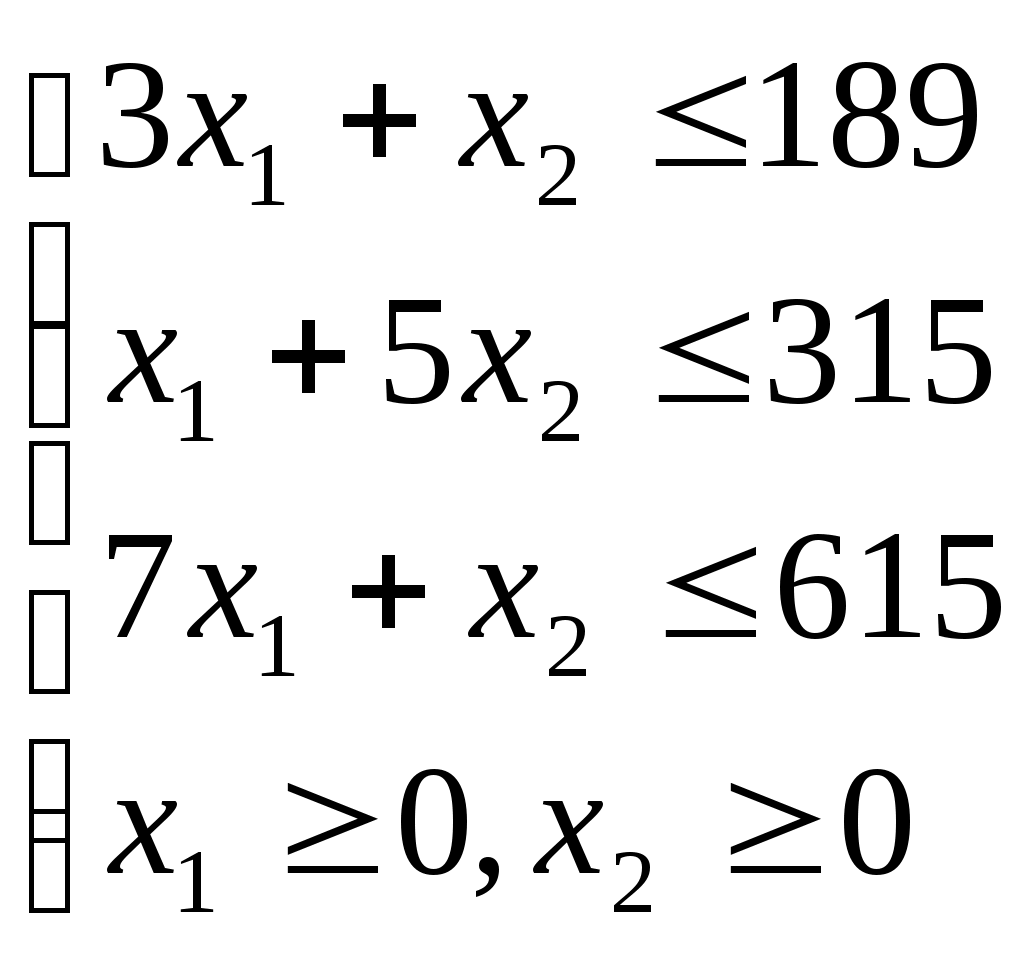 Целевая функция прибыли: Z=196х1+364x2 max 2. Используя графический метод решения задачи линейного программирования, найти оптимальную программу выпуска продукции. Первым шагом в графическом методе решения является построение множества допустимых решений (МДР), для ее построения необходимо построить граничные прямые, уравнения которых получаются из неравенств при замене знака «» на «=». На рис. 1. показано МДР. МДР представляет собой многоугольник OABC. Для нахождения точки максимума целевой функции Z=196х1+364х2 нужно построить градиент функции Z, он равен: 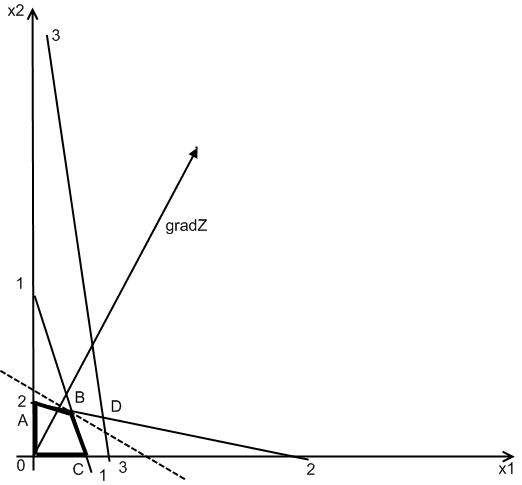 . Из начала координат в направлении к точке (196;364) проводим вектор. Перпендикулярно вектору проводим некоторую прямую, которая будет являться линией уровня линейной функции Z. Двигая линию уровня параллельной самой себе в направлении grad Z, можно найти точку максимума, ей будет являться точка Х* - самая последняя точка МДР, с которой пересечется линия уровня.  Рис. 1. В нашей задаче точкой максимума является точка В, которая лежит на пересечении линий (1) и (2). Её координаты можно найти, решив систему уравнений: 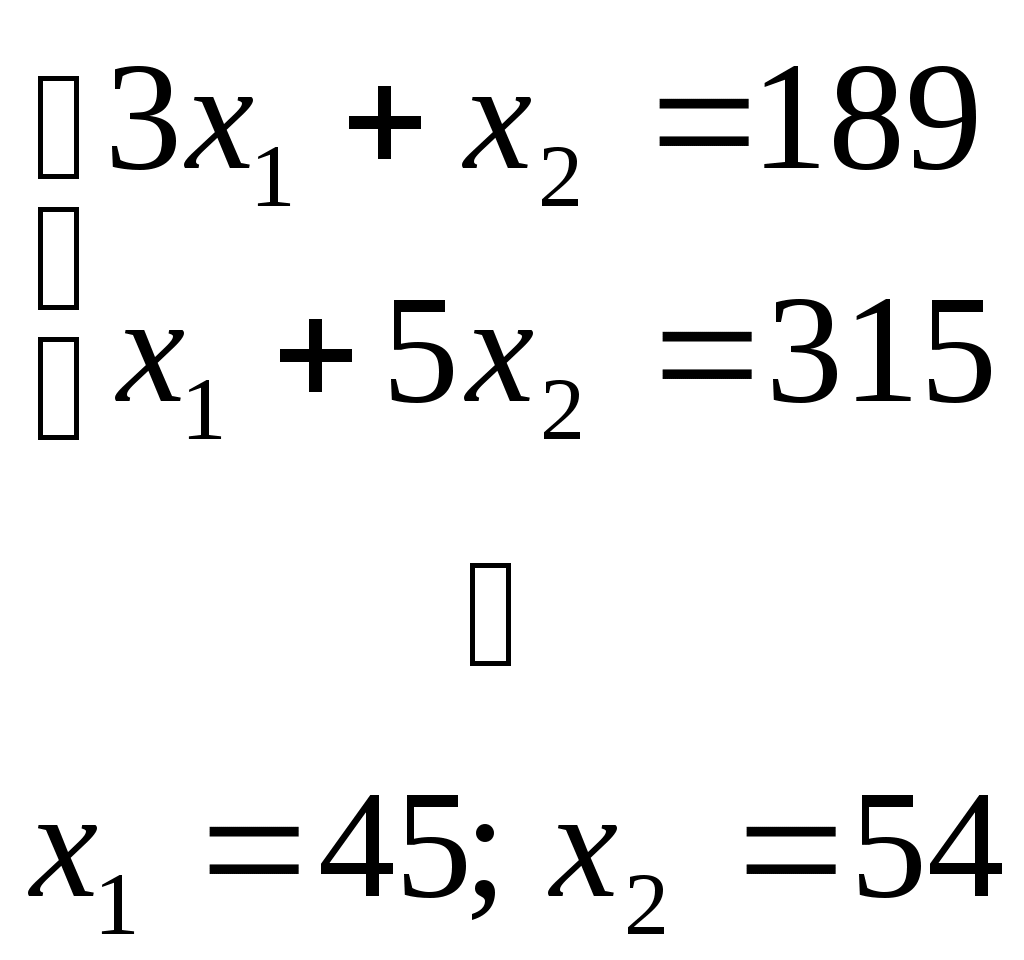 Тогда максимальный доход от реализации изделий А и В составит:  (руб.)Оптимальная производственная программа состоит в выпуске 45 изделия вида А и 54 изделия вида В. 3. Составив задачу, двойственную к задаче оптимизации выпуска продукции, найти ее оптимальное решение, используя условия «дополняющей нежесткости». Дать экономическую интерпретацию этого решения. Каждому ресурсному ограничению исходной задачи сопоставляется двойственная переменная (оценка). Так как в нашей задаче рассматриваются три ресурса, то введем для них три оценки, которые обозначим через u1, u2, u3: 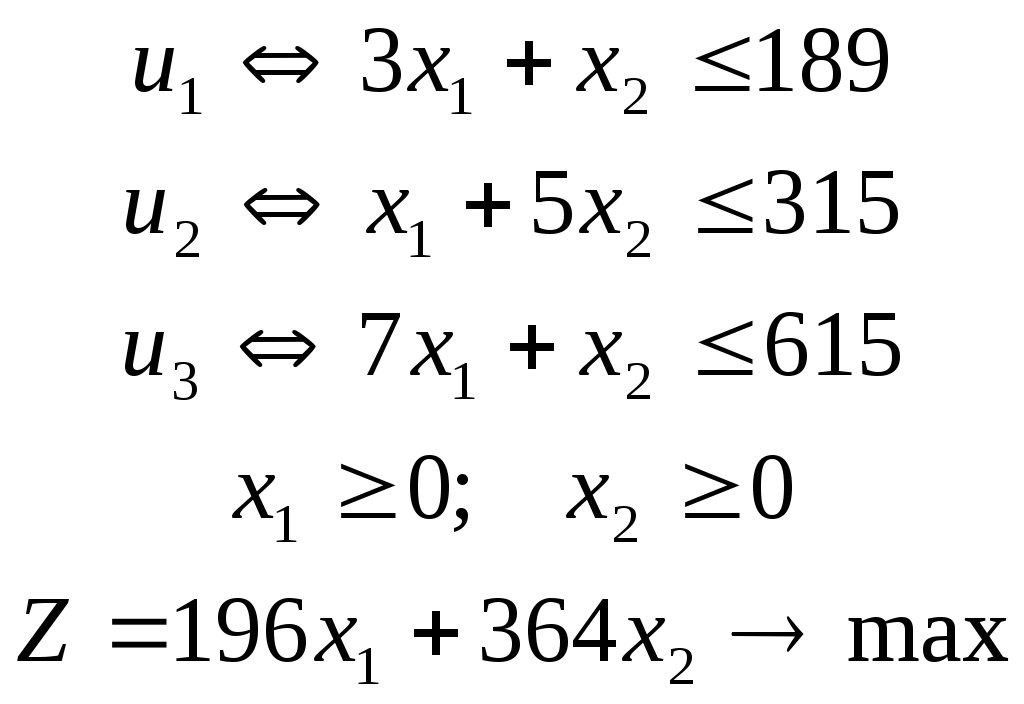 Тогда двойственная задача будет иметь вид: 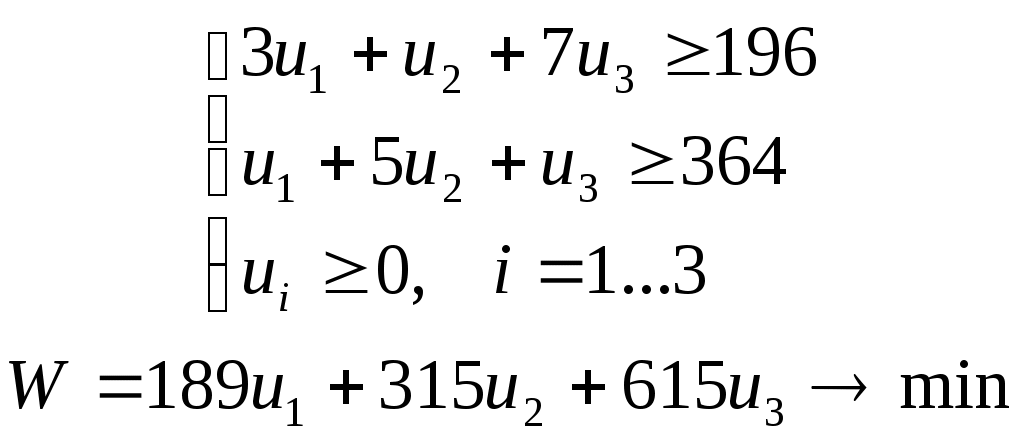 Допустимые решения 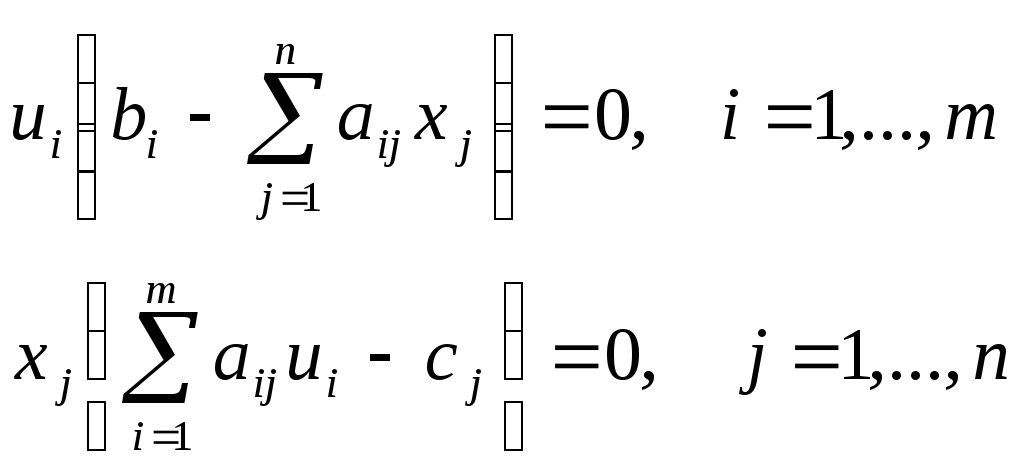 прямой и двойственной задачи оптимальны тогда и только тогда, когда выполняются условия «дополняющей нежесткости»: Для рассматриваемой задачи имеем: 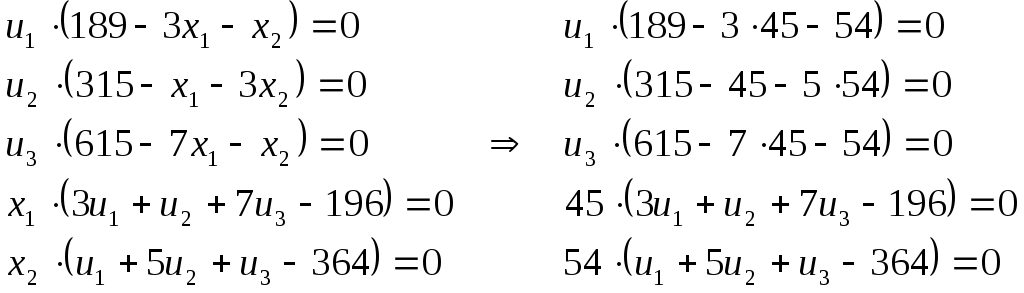 Таким образом, получаем: 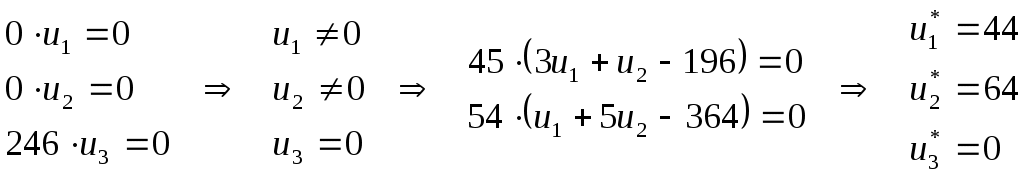 Тогда значение целевой функции двойственной задачи составит:  (руб.), таким образом, значения целевых функций исходной и двойственной задач совпадают.В итоге получили следующие результаты расчета модели: Х*=(45;54); U*=(44;64;0); Z*=W*=28476 Оптимальные двойственные оценки имеют четкую экономическую интерпретацию. Они являются количественной мерой предельной полезности или эффективности использования ресурсов. Оптимальная оценка ресурса характеризует абсолютное увеличение оптимизируемого показателя Z в случае увеличения (снижения) объема этого ресурса на одну единицу. Стоимостная оценка сырья  руб./кг. означает, что при увеличении количества используемого в производстве сырья с 189 кг. до  кг., увеличение максимальной суммарной выручки составит  руб., а при уменьшении сырья на  выручка уменьшится на  руб.Стоимостная оценка времени работы оборудования  руб./ст.-час. означает, что при увеличении месячного фонда времени работы оборудования с 315 ст.-час. до  ст.-час. увеличение максимальной суммарной выручки составит  руб., а при уменьшении фонда времени на выручка уменьшится на  руб.Стоимостная оценка трудовых ресурсов  означает, что ни увеличение, ни уменьшение количества используемых в производстве продукции трудоресурсов не приведет к изменению оптимального значения суммарной выручки. Действительно, количество трудоресурсов для производства оптимальных объемов продукции  составит  чел.час, а предприятие располагает 615 чел.час. трудовых ресурсов. Следовательно,  чел.час. трудоресурсов остаются неиспользованными. Поэтому увеличение или сокращение используемых трудовых ресурсов (но не более, чем на 295 чел.час), не приведет к изменению оптимального значения суммарной выручки.Задача 4 1. Построение сетевого графика выполнения работ: Построение сетевого графика начинается с изображения начального события, которое обозначается цифрой 1, из начального события выпускаются стрелки, соответствующие работам, которым не предшествуют другие работы, в данной задаче начальными работами являются: C, E и V. Все остальные работы в сетевом графике располагаются в зависимости от того, на какие работы они опираются. Начальный вариант сетевого графика приведен на рис. 4.1. На полученном графике есть пара работ, имеющих одни и те же начальные и конечные события – это работы F и A, чтобы избежать этого, введем работу 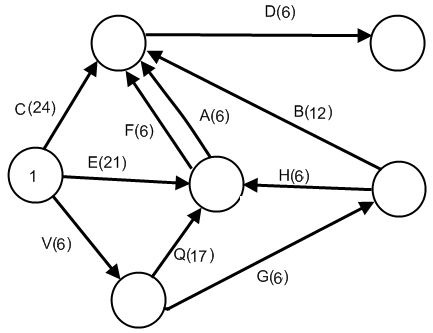 с продолжительностью выполнения 0 дней.  Рис. 4.1. События сетевого графика необходимо пронумеровать таким образом, чтобы номер начального события каждой работы был меньше номера конечного события данной работы На рис. 5.2 приведен упорядоченный сетевой график выполнения работ, в скобках указана продолжительность работ. 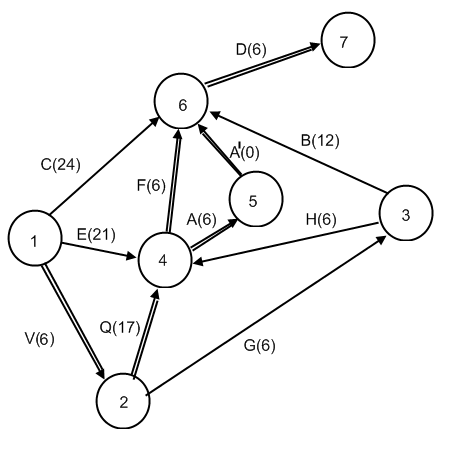 Рис. 4.2. 2. Расчет временных характеристик сетевого графика при нормальном режиме работ. Раннее время наступления i-го события ( 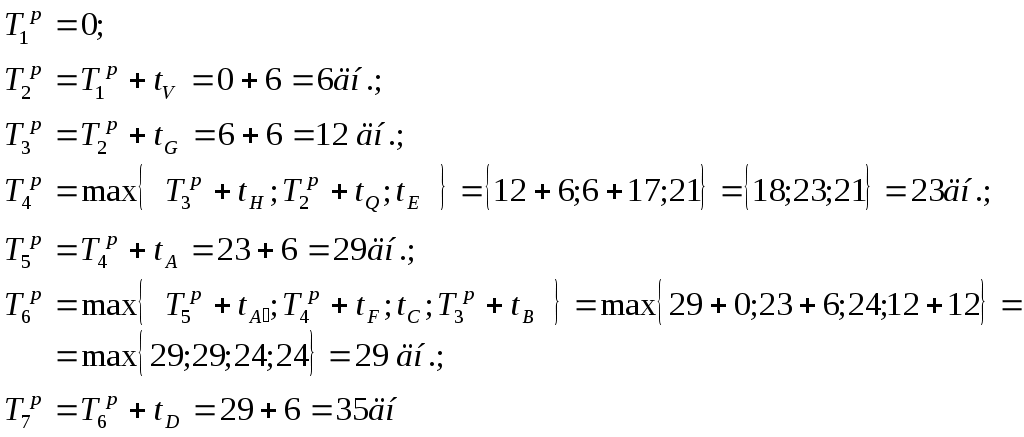 ) – это момент времени, раньше которого событие i не может наступить: Таким образом, ранее время наступления конечного события сетевого графика составляет 35 дней, т.е. раньше, чем за 35 дней, торговый павильон не может быть построен. Следовательно,  .Определим критический путь. Критическое время было найдено по формуле:  , следовательно, работа D, на которую опирается последнее событие, является критической.Для 6 события максимум достигается на работах F и , которые также являются критическими.Для 5 события максимум достигается на работе А, которая также входит в критический путь. Для 4 события максимум достигается на работе Q, т.е. Q – критическая. Работа Q, в свою очередь, опирается на работу V, которая также является критической. Таким образом, имеем два критических пути:  и  с критическим временем Ткр=45 дней. Покажем их на рис. 5.2 двойными стрелками.Стоимость выполнения всего комплекса работ при нормальном режиме их выполнения: Sнор=1,2+4,8+14,4+28,2+90+31,2+0,4+1,6+69,6+36=278 тыс. руб. 3. Ускорение срока строительства на 2 дня. Необходимо сократить период строительства на 2 дня, т.е. вместо 45 дней построить павильон за 43 дня. Дополнительные затраты на один день ускорения рассчитываются по формуле:  где - плата за ускорение работы,   - ее длительности при нормальном и ускоренном режиме выполнения; - стоимость работы при ускоренном и нормальном режимах.Результаты расчетов приведены в таблице:
Сокращение срока строительства будем осуществлять путем ускорения работ, входящих в критический путь. При этом необходимо отслеживать вновь появляющиеся критические пути. Выявим полные пути сетевого графика (рис.4.3) 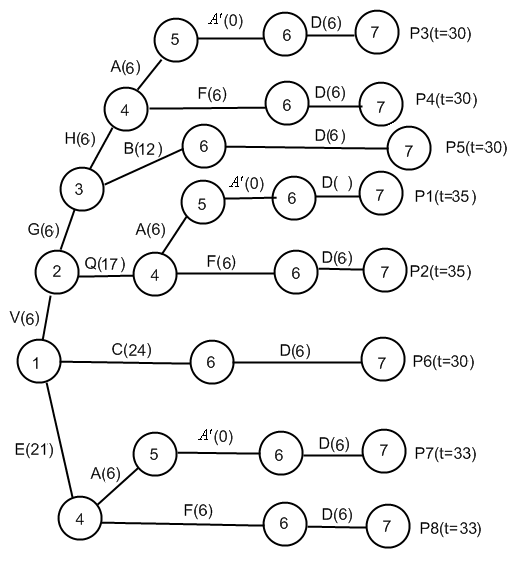 Рис. 4.3. Необходимо уменьшить критический путь  и  на 2 дня.Достаточно сократить время некоторых из работ, входящих в критический путь. Сначала попытаемся уменьшить срок работ на 1 день: Сокращения критического пути на 1 день можно добиться сокращением на 1 день времени выполнения работ Q , V, или D, или одновременным сокращением работ А и F. Сокращение на 1 день работы Q стоит 8,7 тыс. руб. Сокращение на 1 день работы V стоит 9 тыс. рублей Сокращение на 1 день работы D стоит 7,2 тыс. руб. Одновременное сокращение работ F и А стоит 7,8 + 0,3 = 8,1 тыс. руб. Т.е. наиболее выгодно уменьшить на 1 день работу D, при этом критические пути и уменьшится на 1 день, время строительства Ткр= 34 дня. Новых критических путей не появляется.Уменьшим еще на 1 день: Из приведенных выше рассуждений видим, что из оставшихся работ выгоднее сократить еще на 1 день работу D. При этом Ткр=33 дня. Новых критических путей не появляется. Расходы на ускорение составят 7,2 + 7,2 = 14,4 тыс. руб., т.е. стоимость ускоренного строительства павильона  тыс. руб.Сетевой график ускоренного строительства изображен на рис. 4.4. 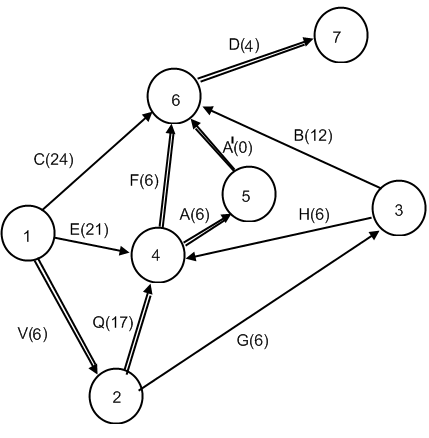 рис.4.3. Итак, в результате решения мы получили: Нормальный режим: Критическое время – 35 дней Критические пути:  и  Стоимость 278 тыс. руб. Ускоренный режим: Критическое время – 33 дня. Критические пути:  и Стоимость 292,4 тыс. руб. 2. Тестовая часть 1 вопрос. Какой из следующих векторов (x1,x2) является решением задачи 1? А. (44,54) Б. (45,55) В. (45,54) Г. (44,57) Ответ: В 2 вопрос. Какая из пар теневых цен (u1,u2) является оптимальной для задачи 1? А. (37,54) Б. (34,54) В. (39,59) Г. (44,64) Ответ: Г 3 вопрос. Какое значение теневой цены u3 является оптимальным для задачи 1? А. 22. Б. 113. В. 0. Г. 54. Ответ: В 4 вопрос. Какова будет предельная эффективность 54-го кг.сырья при заданных в задаче 2 лимитах оборудования и труда (с точностью до 0,1)? А. 243,0. Б. 182,0. В. 364,0. Г. 535,0. Ответ: В 5 вопрос. Какова будет предельная эффективность 176-го кг.сырья при заданных в задаче 2 лимитах оборудования и труда (с точностью до 0,1)? А. 22,0. Б. 0,0. В. 30,0. Г. 44,0. Ответ: Г 6 вопрос. Укажите правую границу интервала устойчивости предельной эффективности сырья, которому принадлежит 54-й кг. сырья (с точностью до 0,1). А. 42,1. Б. 31,1. В. 63,0. Г. 134,0. Ответ: В 7 вопрос. Укажите правую границу интервала устойчивости предельной эффективности сырья, которому принадлежит 176-й кг. сырья (с точностью до 0,1). А. 193,1. Б. 145,0. В. 290,3. Г. 436,3. Ответ: В 8 вопрос. Предприятие имеет возможность продать 95 кг. сырья по цене 267 руб. за килограмм. Укажите какой приблизительный эффект может получить предприятие при этой продаже. А. 800. Б. -959. В. 641. Г. -480. Ответ: А 9 вопрос. Известны фрагменты оптимального плана перевозок для задачи 3: X15 = 56, X24 = 5, X33 = 44. Укажите суммарные транспортные расходы для всего оптимального плана. А. 961. Б. 951. В. 1086. Г. 1046. Ответ: Б 10 вопрос. Какой из предложенных путей является критическим для задачи 4? А. E, Q, F, D, .. Б. C, Q, H, F, D.. В. V, Q, F, H, D.. Г. V, Q, F, D, .. Ответ: Г Список литературы Ашманов С.А. Математические модели и методы в экономике. – М.: Наука, 2009. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем. – М.: Финансы и статистика, 2007. Замков О.О., Толстопятенко А.В. Математические методы в экономике. – М.: ДИС, 2007. Колемаев В.К. Математическая экономика. – М.: ЮНИТИ, 2008. Солодовников А.С. Математика в экономике. – М.: Финансы и статистика, 2008. |