Пространственная задача теплопроводности. Задача теплопроводности
 Скачать 34.56 Kb.
|
|
Пространственная задача теплопроводности. Распространение тепла в шаре Решение задачи теплопроводности в пространстве двух и трех измерений связано с большими трудностями математического характера. Возможности использования математического аппарата в настоящем курсе сильно ограничены. Поэтому рассмотрим краевую задачу для трехмерного пространства, решение которой можно привести к одномерному случаю. Пусть имеем однородный шар радиуса 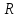 , центр которого находится в начале координат. Предположим, что как в начальный, так и в последующие моменты времени температура одна и та же во всех точках, находящихся на одинаковой расстоянии 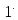 от центра шара. Во все время наблюдения внешняя поверхность шара поддерживается при нулевой температуре. Определим температуру любой точки внутри сферы в момент времени 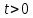 .Преобразуем уравнение теплопроводности в пространстве трех координат 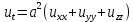 уравнению с одной пространственной координатой, т.к. температура  в точке 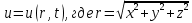 для  по условию зависит от ее расстояния  до начала координат.Значит,  Из предыдущего уравнения найдём 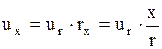  Аналогично определяются 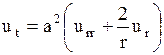 ,  . После подстановки в (1.250) найденных выражений для частных производных  , , уравнение примет вид Тогда начальное условие запишется в виде  ,где  - заданная функция в интервале  , а граничное условие Если ввести новую неизвестную функцию  то задача легко сводится к решенной ранее одномерной краевой задаче с однородными граничными условиями. В самом деле, из первого уравнения найдем  Выразим отсюда  ,  ,  и подставим их значения в первое уравнение u. Уравнение u преобразуется к виду а условия для новой функции  так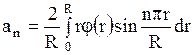овы:   где  Искомая температура  |