КР (вопрос 32). Задача в 68 Обработка результатов равноточных многократных измерений 7 Вопрос 32 Требования, предъявляемые к органам по сертификации, испытательным лабораториям (центрам).

• Название: Задача в 68 Обработка результатов равноточных многократных измерений 7 Вопрос 32 Требования, предъявляемые к органам по сертификации, испытательным лабораториям (центрам).
• Дата: 12.01.2023
• Размер: 90.98 Kb.
• Имя файла: КР (вопрос 32).docx
• Тип: Задача; #882781

Содержание:

Вопрос № 32 Требования, предъявляемые к органам по сертификации, испытательным лабораториям (центрам). 2

Задача – В 68 1. Обработка результатов равноточных многократных измерений 7

Вопрос № 32 Требования, предъявляемые к органам по сертификации, испытательным лабораториям (центрам).

1 Общие сведения об аккредитации

Согласно Федеральному Закону «О техническом регулировании» № 184-ФЗ от 27.12.2002 года аккредитация испытательных лабораторий (центров), выполняющих работы по подтверждению соответствия, осуществляются в порядке, установленном Правительством Российской Федерации.
Испытательная лаборатория – лаборатория, которая проводит испытания.

Аккредитация (испытательной лаборатории) – официальное признание полномочным (авторитетным) органом компетентности (способности) лаборатории проводить конкретные испытания или конкретные виды испытаний в определенной области деятельности.

Система аккредитации – система, обладающая собственными правилами процедуры и управления для осуществления аккредитации объектов.

Аккредитующий орган – орган, который управляет системой аккредитации и проводит аккредитацию организаций, являющихся объектами аккредитации в управляемой им системе аккредитации (в том числе испытательных лабораторий).

2.Аккредитация органов по сертификации и испытательных лабораторий (центров) осуществляется в целях:

- подтверждение компетентности органов по сертификации и испытательных лабораторий (центров), выполняющих работы по подтверждению соответствия;

- обеспечения доверия изготовителей, продавцов и приобретателей к деятельности органов по сертификации и аккредитованных испытательных лабораторий (центров);

- создания условий для признания результатов деятельности органов по сертификации и аккредитованных испытательных лабораторий (центров).

3. Аккредитация органов по сертификации и испытательных лабораторий (центров), выполняющих работы по подтверждению соответствия, осуществляется на основе принципов:

- добровольности;

- открытости и доступности правил аккредитации;

- компетентности и независимости органов, осуществляющих аккредитацию;

- недопустимости ограничения конкуренции и создания препятствий пользованию услугами органов по сертификации и аккредитованных испытательных лабораторий (центров);

- обеспечения равных условий лицам, претендующим на получение аккредитации;

- недопустимости совмещения полномочий на аккредитацию и подтверждение соответствия;

- недопустимости установления пределов действия документов об аккредитации на отдельных территориях.

4. Аккредитация органов по сертификации и испытательных лабораторий (центров), выполняющих работы по подтверждению соответствия, осуществляется в порядке, установленном Правительством Российской Федерации. Требования утверждены постановлением Правительства Российской Федерации от 30 апреля 2019 г. № 546.

4.1. Аккредитация как признание, что физическое лицо или организация обладает достаточной компетенцией для выполнения конкретных работ в области оценки соответствия, - важнейший фактор функционирования системы оценки соответствия.

Он важен

- как для государственных органов, которые заинтересованы в высоком уровне доверия к сертификатам и иным документам, применяемым в этой области,

- так и для самих органов по сертификации, испытательных лабораторий (центров), которым необходимо демонстрировать свою честность, техническую оснащенность и компетентность.

Аккредитация - гарантия непредвзятости, независимости и компетентности.

4.2. Представленные в законе принципы, на основе которых осуществляется аккредитация органов по сертификации и испытательных лабораторий (центров), обусловливают предъявление к аккредитующему органу ряда требований.

Это

- необходимость иметь определенный юридический статус, финансовую стабильность, права и ответственность, обеспечивающие защиту всех сторон, участвующих в деятельности по сертификации;

- необходимость располагать помещениями и средствами труда, необходимыми для его деятельности;

- иметь соответствующую организационную структуру, включающую систему обеспечения качества,

- располагать штатным персоналом, соответствующим направлению и объему работ по аккредитации.

Система обеспечения качества аккредитующего органа должна соответствовать области распространения системы аккредитации.

Она регламентируется Руководством по качеству, которое постоянно актуализируется ответственным сотрудником, подчиняющимся руководству аккредитующего органа.

Аккредитующий орган определяет порядок проведения аккредитации и регистрационных записей, процедуру рассмотрения жалоб.

5. Порядок аккредитации органов по сертификации и испытательных лабораторий (центров), выполняющих работы по подтверждению соответствия, устанавливается Правительством Российской Федерации.

Создаваемая на основе закона система аккредитации в стране будет интегрирована в целях облегчения внешней торговли в европейскую и мировую системы.

В связи с этим комплект документов, регламентирующих систему аккредитации, должен быть гармонизирован с европейскими стандартами серии ЕN 45000.

Серия европейских стандартов ЕN 45000 имеет большое значение для ведения работ по сертификации.

Европейские  стандарты  этой  серии  определяют деятельность  испытательных  лабораторий, органов по  сертификации  продукции,  системкачества, аттестации персонала и изготовителя,   заявляющего о соответствии продукции требованиям стандартов.

Стандарты используют для укрепления доверия к лабораториям, органам по сертификации и декларациям поставщика о соответствии качества оборудования стандартам.

Европейский стандарт ЕN 45001 "Общие требования к деятельности испытательных лабораторий" базируется на руководствах ИСО/МЭК.

Стандарт предусматривает следующие требования для испытательных лабораторий:

- обязательное определение юридического статуса испытательных лабораторий;

- организации должны быть беспристрастными, независимыми и неприкосновенными;

- испытательные лаборатории должны быть компетентными для проведения соответствующих испытаний;

- в рамках организационной структуры они должны иметь технического руководителя, несущего ответственность за выполнение всех задач;

- наличие документированного положения, содержащего направления деятельности лаборатории;

наличие специалистов,  имеющих  соответствующее образование,  технические знания и опыт.

Лаборатории вменяется располагать всей необходимой документацией, касающейся опыта, уровня подготовки и степени квалификации персонала.

Лаборатория

- должна быть оснащена оборудованием для проведения испытаний,

- должна применять методы и процедуры, установленные в документах, в соответствии с которыми испытывают изделия;

- должна иметь систему регистрации результатов испытаний, расчетов, протоколов и систему, устанавливающую правила обращения с образцами, конфиденциальности и безопасности;

- должна сотрудничать с заказчиками и органами по аккредитации, предоставлять возможность их доступа при проведении испытаний и проверок.

Аккредитация регламентируется нормами на процесс ее выполнения и требованиями, предъявляемыми к органу по аккредитации.

Процесс аккредитации органов по сертификации установлен в стандарте ЕN 45002 "Общие требования при оценке (аттестации) испытательных лабораторий".

Деятельность органов по аккредитации регламентируется в стандарте ЕТ 45003 "Общие требования к органам по аккредитации лабораторий".

Стандарт ЕТ 45011 "Общие требования к органам по сертификации, проводящим сертификацию продукции" основан на международных документах по сертификации продукции.

Стандарт устанавливает основные положения, которым должен соответствовать орган по сертификации, чтобы быть признанным на национальном или европейском уровне.

Орган по сертификации должен быть беспристрастным и иметь:

- организационную схему, определяющую взаимодействие между испытательными, контрольными и сертификационными функциями;

- сведения об источниках финансирования;

- документированное описание учрежденных им систем сертификации, включающих основные правила и процедуры;

- документацию, определяющую его юридический статус.

Орган по сертификации должен

- иметь сведения о подготовке и профессиональном опыте персонала,

- иметь систему регистрации и протоколирования каждой процедуры сертификации, включая отчеты об испытаниях и инспекционном контроле.

Деятельность по испытаниям, которую осуществляет орган по сертификации, должна удовлетворять требованиям стандартов ЕN 45001 и ЕN 45002.

Орган по сертификации действует на основе руководства по качеству и обязан контролировать использование выданных им лицензий, сертификатов и знаков соответствия.

Обязательным условием функционирования органов по сертификации и испытательных лабораторий является соответствие нормам, регламентирующим их деятельность.

Требования к органам по сертификации заложены в стандарте ЕN 45012 "Общие требования к органам по сертификации, проводящим сертификацию систем обеспечения качества".

Стандарт ЕТ 45013 "Общие требования к органам по сертификации, проводящим аттестацию персонала" устанавливает общие требования, которые орган по аттестации должен соблюдать при аттестации персонала.

Орган по аттестации должен иметь:

- организационную схему, которая устанавливает связь между функциями по оценке и аттестации;

- сведения об источниках финансирования;

- документацию внутренней системы качества;

- документацию, определяющую его юридический статус.

Орган по аттестации должен располагать письменной информацией о квалификации, подготовке и профессиональном опыте каждого сотрудника.

Орган по аттестации должен иметь систему документации, регистрации каждой процедуры аттестации и контроля за аттестованным персоналом и руководство по качеству.

Он должен вести перечень аттестованных сотрудников, который должен быть доступен общественности с указанием области аттестации для каждого сотрудника, а также осуществлять контроль за использованием своих сертификатов компетентности.

Европейский стандарт ЕN 45014 "Общие требования к декларации поставщика о соответствии" устанавливает определенные требования к декларациям поставщиков.

Согласно этому стандарту поставщик может заявлять под свою ответственность о том, что его продукция находится в соответствии с конкретно обозначенным стандартом.

Поставщик должен контролировать все виды своей деятельности, влияющие на качество продукции, чтобы обеспечить безусловное выполнение всех требований нормативных документов, на которые он ссылается в декларации.

Декларирование производителя о соответствии товара требованиям установленных норм приобретает все большее значение.

Задача – В 68
1. Обработка результатов равноточных многократных измерений

Обработка результатов равноточных многократных измерений с получением среднего арифметического X, среднеквадратичного отклонения Sx, и определением суммарной погрешности измерения в виде доверительного интервала– ±ΣΔРд.

Исходные данные:

1	103,170	11	103,110	21	103,070	31	103,130	41	103,110	51	103,210
2	103,110	12	103,130	22	103,230	32	103,110	42	103,110	52	103,070
3	103,090	13	103,150	23	103,180	33	103,070	43	103,190
4	103,120	14	103,010	24	103,090	34	103,150	44	102,990
5	102,970	15	103,100	25	103,130	35	103,090	45	103,110
6	103,110	16	103,110	26	103,110	36	103,130	46	103,090
7	103,070	17	103,170	27	103,150	37	103,050	47	103,070
8	103,090	18	103,130	28	103,080	38	103,090	48	103,170
9	103,140	19	103,050	29	103,130	39	103,150	49	103,170
10	103,090	20	103,080	30	103,030	40	103,060	50	103,050

Цена деления прибора С, мм - 0,010

Результаты измерений, мм:

Доверительная вероятность Рд = 0,83 - показывает вероятность нахождения истинного значения в рассчитанном интервале.

Уровень значимости q = 0,01 - показывающий, что принятый закон рассеивания размеров не будет соответствовать реальному закону.

Сортируем значения по возрастанию:

1	102,97	11	103,07	21	103,09	31	103,11	41	103,15	51	103,21
2	102,99	12	103,07	22	103,09	32	103,11	42	103,15	52	103,23
3	103,01	13	103,07	23	103,10	33	103,12	43	103,15
4	103,03	14	103,08	24	103,11	34	103,13	44	103,15
5	103,05	15	103,08	25	103,11	35	103,13	45	103,17
6	103,05	16	103,09	26	103,11	36	103,13	46	103,17
7	103,05	17	103,09	27	103,11	37	103,13	47	103,17
8	103,06	18	103,09	28	103,11	38	103,13	48	103,17
9	103,07	19	103,09	29	103,11	39	103,13	49	103,18
10	103,07	20	103,09	30	103,11	40	103,14	50	103,19

1. Построение гистограммы

Определяем величину размаха R (поле рассеяния):

R = Xmax - Xmin=103,23-102,97=0,26

Xmax = 103,23- наибольшее из измеренных значений

Xmin = 102,97 - наименьшее из измеренных значений

R = Xmax - Xmin = 0,26 (мм).

Определяем число интервалов разбиения n

Вв соответствии с рекомендациями(ближайшее нечетное число)

n ===7,2?7.

Количество интервалов принимается ближайшим большим нечетным.

Принимаем n = 7.

Определяем ширину интервала h:



h ===0,037

Определяем границы интервалов Xmin - Xmax

1 интервал: Xmin1 - Xmax1

Xmin1 = Xmin=102,97 мм

Xmax1 = Xmin1 + h = 102,97+0,037=103,007 мм

2 интервал: Xmin2 - Xmax2

Xmin2 = Xmax1 = 103,007 (мм)

Xmax2 = Xmin2 + h = 103,007+0,037=103,044 (мм)

3 интервал: Xmin3 - Х max3

Xmin3 = Xmax2 = 103,044 (мм)

Xmax3 = Xmin3 + h = 103,044+0,037=103,081 (мм)

4 интервал: Xmin4 - Xmax4

Xmin4 = Xmax3 = 103,081 (мм)

Xmax4 = Xmin4 + h = 103,081+0,037=103,118 (мм)

5 интервал: Xmin5 - Xmax5

Xmin5 = Xmax4 = 103,118 (мм)

Xmax5 = Xmin5 + h = 103,118+0,037=103,155(мм)

6 интервал: Xmin6 - Xmax6

Xmin6 = Xmax5 = 103,155 (мм)

Xmax6 = Xmin6 + h = 103,155+0,037=103,192 (мм)

7 интервал: Xmin7 - Xmax7

Xmin7 = Xmax6 = 103,192 (мм)

Xmax7 = Xmin7 + h = 103,192+0,037=103,229=103,23 (мм)

Определяем середины интервалов Xoi

1 интервал:



Xo1 = Xmin1 + h/2=102,97 +0,0185=102,9885 (мм)

2 интервал:

Xo2 = Xmin2 + h/2 = 103,007+0,0185=103,0255 (мм)

3 интервал:

Xo3 = Xmin3 + h/2 = 103,044+0,0185= 103,0625 (мм)

4 интервал:

Xo4 = Xmin4 + h/2= 103,081+0,0185= 103,0995 (мм)

5 интервал:

Xo5 = Xmin5 + h/2 = 103,118+0,0185=103,1365 (мм)

6 интервал:

Xo6 = Xmin6 + h/2 = 103,155+0,0185= 103,1735 (мм)

7 интервал:

Xo7 = Xmin7 + h/2= 103,192+0,0185= 103,2105 (мм)

Определение количества размеров попадающих в каждый интервал mi

Используя заданную выборку, подсчитываем количество размеров попадающих в каждый интервал (если размер совпадает с границей интервала то его относят в интервал, находящийся слева по числовой оси).

Результаты выполненных выше расчетов занесем в таблицу:

Номер интервала	Границы интервала			Середина интервала Xoi (ММ)		Число размеров в интервале, mi
	Xmin (мм)	Xmax (мм)
1	102,97	103,007	102,9885		3		0,057
2	103,007	103,044	103,0255		3		0,057
3	103,044	103,081	103,0625		10		0,192
4	103,081	103,118	103,0995		18		0,346
5	103,118	103,155	103,1365		12		0,230
6	103,155	103,192	103,1735		4		0,076
7	103,192	103,23	103,2105		2		0,038

Используя табличные данные, строим гистограмму рассеивания единичных замеров и теоретическую кривую нормального распределения:



Рис. 1



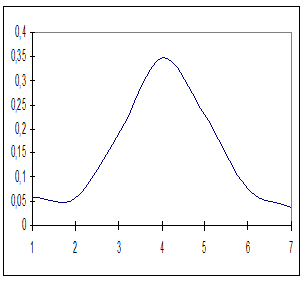
Рис. 2

2. Проверка выборки на соответствие нормальному закону распределения

При числе измерений свыше 50 проверка распределения на соответствие нормальному закону может выполняться по критерию Пирсона. При использовании этого критерия определяется параметр хи-квадрат по следующей формуле:



,

где Noi - теоретическая частота попадания в интервал.

Теоретическая частота попадания в интервал определяется по формуле:



ц(z) - плотность вероятности появления размеров в каждом интервале;

уx - среднеквадратичное отклонение размеров (СКО) выборки.

Считая, что СКО практически совпадает с его оценкой (уx ? Sx) приведем формулу, по которой определяется оценка СКО:



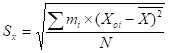
В данную формулу входит величина , которая представляет среднеарифметическое значение измеряемой величины и определяется по формуле:

 

X=1/52 x (103,9885 х 3 + 103,02553 х 3 + 103,0625 х 10 +103,0995 х 18 + 103,1365 х 12 + 103,1735 х 4 + 103,2105 х 2)=103,158

После подстановки 103,158 мм получим численные значения среднеарифметического и оценки СКО:

Sx=0,05 мм Х= 103,158 мм

Кроме полученных величин, для определения теоретической частоты попадания в интервал Noi необходимо знать плотность вероятности попадания размеров в каждом интервале.

Эту величину можно определить по формуле:



Так как расчеты по данной формуле достаточно сложны, значения плотности вероятности выбирают из таблицы в зависимости от безразмерного параметра Z, который для каждого интервала определяется по формуле:



Для 1 интервала:

Zo1 = -3,39 ,

что соответствует величине ц(z) = 0,012

Для 2 интервала:

Zo2 = -2,65

что соответствует величине ц(z) = 1,5

Для 3 интервала:

Zo3 = -1,91,

что соответствует величине ц(z) = 1,39

Для 4 интервала:

Zo4 = -1,17 ,

что соответствует величине ц(z) = 0,44

Для 5 интервала:

Zo5 = -0,43 ,

что соответствует величине ц(z) = 0,24

Для 6 интервала:

Zo6 = 0,03,

что соответствует величине ц(z) = 0,22

Для 7 интервала:

Zo7 = 1,05,

что соответствует величине ц(z) = 0,39

Определяем теоретические значения количества деталей для каждого интервала Noi.



Для 1 интервала:

No1 =0,46

Для 2 интервала:

No2 = 57,72

Для 3 интервала:

No3 =53,48

Для 4 интервала:

No4 =16,93

Для 5 интервала:

No5 = 9,23

Для 6 интервала:

No6 = 8,46

Для 7 интервала:

No7 = 15,007

На основании результатов измерений и расчета теоретических данных определяем фактическую и теоретическую частоту попадания размеров в интервал:

№ интервала	Фактическая чистота	Теоретическая чистота
1	0,057	0,025
2	0,057	0,097
3	0,192	0,222
4	0,346	0,295
5	0,230	0,226
6	0,076	0,100
7	0,038	0,025

Полученные результаты позволяют получить расчетную величину параметра хи-квадрат:

№ интервала	Фактическая частота	Теоретич. Частота
1	0,057	0,025	0,025	0,00063	0,025
2	0,057	0,098	0,098	0,00960	0,098
3	0,192	0,22	0,227	0,05153	0,234
4	0,346	0,295	0,295	0,08703	0,295
5	0,230	0,226	0,217	0,04709	0,208
6	0,076	0,100	0,109	0,01188	0,118
7	0,038	0,025	0,031	0,00097	0,038

 

Для совпадения фактического закона распределения с теоретическим законом нормального распределения необходимо, чтобы выполнялось следующее условие:



где - теоретическое граничное значение параметра хи-квадрат, которое определяется по таблице (таблица 2 задания к контрольной работе).

Для получения табличного значения необходимо определиться с двумя параметрами:

• 
  - уровнем значимости q, который показывает вероятность того, что законы не совпадут (q = 0,01)
  
• 
  - числом степеней свободы , которое определяется в зависимости от числа интервалов n и числа определяемых по статистике параметров, необходимых для совмещения модели и гистограммы r.
  

Для нормального закона распределения r = 2, так как закон однозначно характеризуется двумя параметрами - СКО и МО (математическим ожиданием). Число степеней свободы определяется по формуле:

0,0102

Таким образом, табличное значение .

3. Определение доверительного интервала рассеивания случайных погрешностей вокруг среднего значения

В доверительном интервале, который предстоит найти с вероятностью Рд, должно находится истинное значение измеряемой величины.

Доверительные границы случайной погрешности находятся по формуле:

где - оценка СКО среднего арифметического значения, которая определяется по формуле:

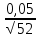=0,007

Если условие выполняется, то гипотеза о совпадении экспериментального и выбранного теоретического (нормального) распределения принимается (она не противоречит данным).

Так как по условию Рд = 0,83, то значение функции Лапласа:

F(Zp) = 0,83

Из таблицы определяем величину нормированного параметра Zp, которая соответствует данному значению функции Лапласа

Zp = 0,415

Таким образом, доверительный интервал случайной ошибки:

^{= ±0,0028}

Перед определением суммарной погрешности определим ее постоянные неисключенные составляющие.

Постоянные неисключенные составляющие:

- погрешность снятия показаний со шкалы (принимается равной цене деления шкалы прибора):

мм,

где С = 0,010 мм - цена деления шкалы прибора;

- систематическая неисключенная погрешность округления результата:



- неисключенная погрешность прибора (условно принимается равной цене деления шкалы прибора:

Суммирование частных постоянных погрешностей измерения производится по двум формулам:

распределение закон погрешность измерение



где k - поправочный коэффициент, зависящий от числа слагаемых погрешностей и доверительной вероятности. В нашем случае k = 0,99

Тогда



Для дальнейшего расчета принимаем (выбирается наибольшее значение).

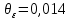мм

В качестве общей случайной погрешности принимаем величину доверительного интервала, полученную из экспериментов по замерам параметра:

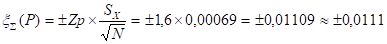^{0,0028 х 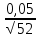= ± 0,00019}

Определение суммарной погрешности измерения:



В качестве окончательного результата принимаем большее значение.

Результат в общем виде: 103,158±0,01419