образцы вопрососв к экзамену. Образцы задач к экзамену. Задача в таблице приведены данные о недельном спросе и предложении на рынке кроссовок

• Название: Задача в таблице приведены данные о недельном спросе и предложении на рынке кроссовок
• Анкор: образцы вопрососв к экзамену
• Дата: 25.05.2023
• Размер: 103.85 Kb.
• Имя файла: Образцы задач к экзамену.docx
• Тип: Задача; #1158930

Тема. Рыночная система: спрос, предложение и рыночное равновесие

Задача 1. Функция предложения на товар имеет вид: Q_D = 30 – P, где Q_D – величина спроса на товар за (шт.), Р – цена за одну штуку. Функция предложения описана следующим уравнением: Q_S = 15 + 2P, где Q_S – величина предложения за день (шт.).

Определите эластичность спроса и предложения в точке равновесия.
Задача 2. В таблице приведены данные о недельном спросе и предложении на рынке кроссовок:

Цена, руб.	1300	1200	1000	900	800	700	600	500
Требуемое количество, тыс. шт.	4	5	6	7	8	9	10	11
Поставляемое количество, тыс. шт.	10	9	8	7	6	5	4	3

а) какими будут равновесные цена и количество товара?

б) предположим, что из-за изменения моды спрос на кроссовки вырос на 2 тыс. шт. при любой цене. Какими будут новые равновесные цена и количество товара? Изобразите изменения на рынке графически.
Задача 3. На спрос некоторый товар описывается формулой: Qd = 16 – 2P, где Qd – величина спроса на товар (шт.), Р – цена за одну штуку (руб.). а его предложение – Qs = 1 + 3Р, где Qs – величина предложения товара. Определите параметры первоначального равновесия. Какая ситуация установится на рынке, если государство установит минимальную цену в 5 руб.? Изобразите изменения на рынке графически.
Задача 4. Спрос и предложение товара выражаются функциями: Qd = 44 – 3P, Qs = 4 + 2Р, где Qd – величина спроса на товар (шт.), Qs – величина предложения товара (шт.), Р – цена за одну штуку (руб.).

Определите равновесную цену и количество товара, которое может быть куплено по равновесной цене. Как изменится объем продаж при установлении государством цены на товар в размере 6 руб.? Изобразите изменения на рынке графически. Как изменится излишек потребителя и производителя? Покажите в виде фигур.
Тема. Поведение потребителя в рыночной экономике

Задача 1.

Найти недостающие данные в таблице, написать формулы расчетов, нарисовать графики всех показателей и объяснить их форму и взаимосвязь.

Q	TU	MU
1	33
2		21
3		10
4	64
5		–9

Задача 2. Используя нижеследующие данные и данные из таблицы:

а) рассчитать количество походов в кино, кафе и музей, при котором будет достигнуто наиболее оптимальное равновесие потребителя, в условиях ограниченности бюджета;

б) сделать выводы:

- останутся ли не потраченные деньги в условиях равновесия или нужно будет использовать накопления прошлых периодов;

- что изменится, если ежемесячный доход сократится в 2 раза;

- о вкусах потребителя и его отношению к деньгам (расточительный, экономный и т.д.).

Месячный доход, предназначенный на развлечение – 5000 руб.

Разовые расходы: на кино – 600 руб., кафе – 700 руб., музей – 200 руб.

Данные о предпочтениях потребителя за месяц

Количе-ство походов	КИНО			КАФЕ				МУЗЕЙ
	TU	MU	MU/P	TU	MU	MU/ P	TU		MU	MU/ P
1	1500			2100			400
2	2700			3500			600
3	3300			4550			700
4	3600			5250			750
5	3780			5600			700

Тема. Производство экономических благ. Издержки производства

Задача 1. Заполните все пустые ячейки таблицы и ответьте на вопросы: при каком объеме производства фирма достигнет своего технологического оптимума? Что это означает? Решение проиллюстрируйте графически.

Q	FC	VC	TC	AFC	AVC	ATC	MC
шт.	руб.	руб.	руб.	руб./шт.	руб./шт.	руб./шт.	руб./шт.
0	50	0		-	-	-	-
10			210
20		250
30							7
40		420				11,75
50					11,4

Задача 2. Зависимость совокупных издержек от объема выпуска фирмы представлена в таблице. Заполните все пустые ячейки таблицы и ответьте на вопросы: при каком объеме производства фирма достигнет своего технологического оптимума? Что это означает? Решение проиллюстрируйте графически.

Q	0	10	20	30	40	50
ТС	100	300	420	600	9200	1250
АТС	-
FC
AFC
VC
АVC
MC

Задача 3. Фирма производит костюмы и затрачивает на один костюм материалов на 4000 руб., рабочего времени - 4 часа при зарплате 250 руб. в час. Также фирма несет постоянные издержки на аренду, зарплату административному персоналу и прочее в размере 180000 руб. в месяц. Определите, сколько костюмов необходимо произвести и продать фирме за месяц, чтобы быть безубыточной, если цена костюма 8000 руб.
Задача 4. Автор хочет издать свою книгу. Средние совокупные издержки описываются уравнением: АТС=150+15000/Q. Цена одной книги предполагается равной 250 руб. Определите размер тиража.
Задача 5. 1) Подпишите недостающие названия функций на графике. 2) Отметьте уровень объема производства, соответствующий технологическому оптимуму. 3) Рассчитайте следующие величины при технологическом оптимуме фирмы (запишите формулы): общие издержки фирмы TC, постоянные издержки фирмы FC, переменные издержки фирмы VC.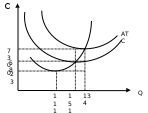


Задача 6. Подпишите функции на графике. Отметьте уровень объема производства, соответствующий технологическому оптимуму. Покажите в виде заштрихованных прямоугольников величину общих постоянных издержек TFC и общих переменных издержек TVC при уровне объема производства, соответствующего технологическому оптимуму.

В чем отличие понятия «технологического оптимума» от понятия «минимально эффективного размера предприятия»? Какие факторы оказывают влияние на эти величины?

Рассчитайте следующие величины при технологическом оптимуме фирмы (обязательно напишите формулы):

1. 
   Общие издержки фирмы TC
   
2. 
   Постоянные издержки фирмы FC
   
3. 
   Переменные издержки фирмы VC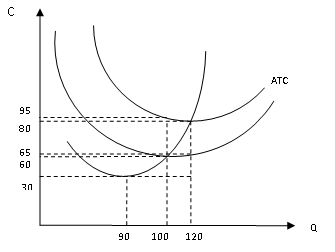
   

Задача 7.

Подпишите функции на графике. Отметьте уровень объема производства, соответствующий технологическому оптимуму. Покажите в виде заштрихованных прямоугольников величину общих постоянных издержек TFC и общих переменных издержек TVC при уровне объема производства, соответствующего технологическому оптимуму.

В чем отличие понятия «технологического оптимума» от понятия «минимально эффективного размера предприятия»? Какие факторы оказывают влияние на эти величины?

Рассчитайте следующие величины при технологическом оптимуме фирмы (обязательно напишите формулы):

1. 
   Общие издержки фирмы TC
   
2. 
   Постоянные издержки фирмы FC
   
3. 
   Переменные издержки фирмы VC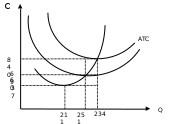
   

Задача 8. Подпишите функции на графике. Отметьте уровень объема производства, соответствующий технологическому оптимуму. Покажите в виде заштрихованных прямоугольников величину общих постоянных издержек TFC и общих переменных издержек TVC при уровне объема производства, соответствующего технологическому оптимуму.

В чем отличие понятия «технологического оптимума» от понятия «минимально эффективного размера предприятия»? Какие факторы оказывают влияние на эти величины?

Рассчитайте следующие величины при технологическом оптимуме фирмы (обязательно напишите формулы):

1. 
   Общие издержки фирмы TC
   
2. 
   Постоянные издержки фирмы FC
   
3. 
   Переменные издержки фирмы VC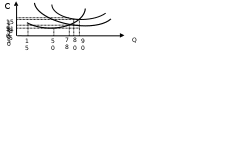
   

Тема. Фирма как совершенный конкурент

Задача 1. Цена одной единицы продукции равна 3 тыс. руб, функция издержек фирмы, действующей на рынке совершенной конкуренции, имеет вид TC(Q)=1/2Q²+Q. Определить объем производства, при котором прибыль фирмы максимальна, и найти прибыль на единицу продукции при этом объеме.
Задача 2. В отрасли совершенной конкуренции функция предложения определена как Qs=1 + 3P, а функция спроса Qd=46 – 2Р. У одной из фирм отрасли функция общих издержек выражена как TC=0,5q² – q. Определите при какой цене и каком объеме производства фирма максимизирует прибыль? Рассчитайте размер прибыли.
Задача 3. Для фирмы, действующей в условиях совершенной конкуренции, на рис.1 представлены кривые средних (ATC) и предельных (MC) издержек. На рис. 2 показаны: рыночный спрос (D) и рыночное предложение (S). Используя данные рисунков, определите размер прибыли или убытка (в ден. ед.), получаемой фирмой в краткосрочном периоде.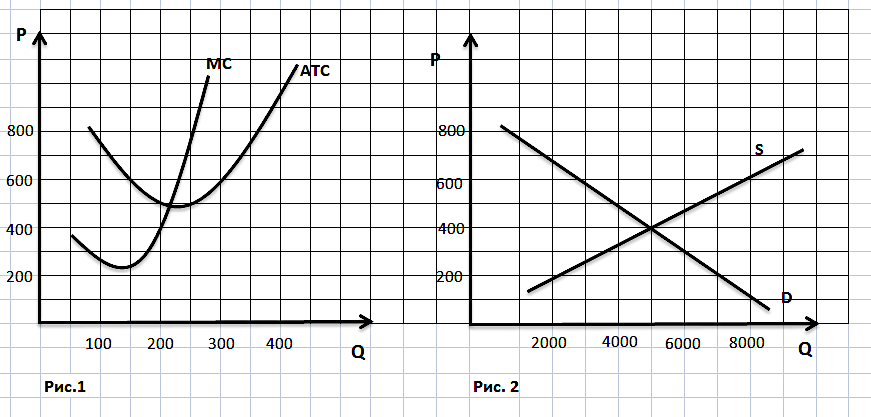


Задача 4. Общие издержки производства фирмы - совершенного конкурента представлены в таблице (в рублях). Какой объем производства выберет фирма при сложившейся цене 15 рублей за 1 ед.? При данной цене и данном объеме фирма будет максимизировать прибыль или минимизировать убытки. Определите размер прибыли (убытка).

Q	0	10	20	30	40	50	60
TC	50	210	300	370	470	620	840
МС
ATC
TVC
AVC

Задача 5. Фирма - совершенный конкурент максимизирует прибыль при объеме производства 50 единиц. Функция общих издержек фирмы имеет вид: TC=5q²+20q. Определите рыночную цену продукта и прибыль фирмы.
Задача 6. В конкурентной отрасли действуют 32 одинаковых фирмы. Спрос на продукцию в отрасли задан функцией Qd=68–P (тыс. т). Общие издержки каждой фирмы описываются функцией: TC=4q²+8q (руб.). Определите равновесную цену и объем производства каждой фирмы.
Задача 7. Фирма - совершенный конкурент имеет функцию общих издержек TC=0,03Q³-3Q²+90Q+900. Определите при какой цене фирма продолжит производство в краткосрочном периоде.
Задача 8. Фирма, действующая на рынке совершенной конкуренции, имеет затраты на производство 100000 руб., а реализует товар по цене 1000 руб. Какое количество продукции (в шт.) необходимо выпускать фирме, чтобы получать нормальную прибыль?
Задача 9. Общие издержки фирмы, действующая в условиях совершенной конкуренции, представлены функцией TC= 3Q²–90Q+700. При оптимальном объеме производства фирма получает прибыль 500 руб. Определите рыночную цену и оптимальный объем продукции данной фирмы (в шт.).

Тема. Монополия и антимонопольное регулирование

Задача 1. Если функция спроса на продукцию монополиста описывается уравнением P = 140–5Q (тыс. руб.), а функция общих издержек TC = 150+2Q² (млн т), то при какой цене и объеме продаж он получит максимальную прибыль?
Задача 2. Фирма выпускает товар в условиях монополии. Функция спроса на ее товар описывается формулой: Р = 200 – 6Q (руб.), а функция общих издержек:

ТС = 300 + 80Q (руб.). При каком объеме выпуска (млн т) прибыль будет максимальной?
Задача 3. Кривая спроса на товар фирмы-монополиста описывается функцией

Q_d = 600 – 3Р. Какую цену следует установить на данную продукцию с целью максимизации общей выручки от продажи товара?
Задача 4. В таблице дана зависимость общих издержек от объема производства и функция спроса фирмы монополиста.

Выпуск	Общие издержки	Средние общ издержки	Предельные издержки	Цена	Общий доход	Предельный доход	Прибыль
Q	TC	ATC	MC	P	TR	MR	Prof
0	285			380
1	494			332,5
2	608			285
3	695,4			256,5
4	760			228
5	845,5			199,5
6	969			171

Выполните следующие задания:

1. 
   Найдите оптимальные цену, объем фирмы и максимальную прибыль. Расчеты занесите в таблицу.
   
2. 
   Нарисуйте равновесие фирмы монополиста в модели «общий доход – общие издержки» и в модели «предельный доход – предельные издержки» (без масштаба, общие модели) Покажите на графиках рассчитанные параметры оптимума.
   
3. 
   В чем преимущества и недостатки двух моделей?
   
4. 
   Какие социально-экономические последствия создает монополия?
   

Тема. Монополистическая конкуренция и олигополия.

Задача 1. На рынке работают три фирмы, имеющие одинаковый размер. Предельные издержки фирм одинаковы, постоянны и составляют 1200 руб. Отраслевой спрос на продукцию представлен функцией: Р = 6000 – 2Q, где Р – цена, руб. за ед., а Q – величина спроса, тыс. шт. Фирмами принято решение - объединиться в картель и разделить рынок поровну. Определить равновесную цену и объем производства продукции для каждой фирмы.

Задача 2.

На рынке дуополии рыночный спрос представлен следующей функцией: Q = 195 – 2,5P. Товар продают две фирмы А и В. Уравнения их реакции на выпуск конкурента: q_A = 60 - 0,4q_B, q_B = 80 – 0,5q_A. Определить цену, по которой будет продаваться товар.

Задача 3. В маленьком туристическом городе существует 5 фирм, где можно взять напрокат машину. Совокупные издержки каждой их них представлены в виде: ТСi=0,9Q². Рыночный спрос на эту услугу описывается уравнением Q=1000–2P. Если все эти фирмы объединятся в картель, какой будет цена на прокат автомобилей? Сколько будет машин в каждой фирме?
Задача 4. Функция издержек фирмы – монополистического конкурента ТC=3Q²+200Q+700. Функция спроса Q=250–0,5P. Определите равновесные объем выпуска и цену и подсчитайте размер прибыли фирмы.
Тема. Рынок труда и распределение доходов.

Задача 1. Спрос на труд описывается следующим уравнением: Ld=50-5W, предложение: Ls=10W–5, где W – ставка заработной платы, L – количество работников. Найдите параметры равновесия и определите уровень вынужденной безработицы, если минимальная ставка заработной платы будет равна 5. Приведите графическую иллюстрацию решения.
Задача 2. Кондитерская выпекает торты и на некотором отрезке времени может изменять количество только одного ресурса — число занятых работников, которые нанимаются на совершенно конкурентном рынке труда. Другие факторы остаются неизменными. Функция предельного продукта труда МР_L = 250 – 5L. Цена тортов на совершенно конкурентном рынке P = 500 руб.

1. Рассчитайте, сколько работников следует нанять фирме, чтобы максимизировать прибыль, если ставка заработной платы каждого рабочего составляет 40000 руб. в месяц?

2. Если цена торта уменьшится до 400 руб., как изменится число работников, которых сможет нанять фирма для максимизации прибыли.

3. Как изменится число нанимаемых работников на данной фирме, в случае увеличения цены труда на конкурентном рынке до 45000 руб.
Задача 3. Спрос на труд описывается следующим уравнением: Ld=50-5W, предложение: Ls=10W–5, где W – ставка заработной платы, L – количество работников. Найдите параметры равновесия и определите уровень вынужденной безработицы, если минимальная ставка заработной платы будет равна 5. Приведите графическую иллюстрацию решения.
Задача 4. Фирма является монополистом на рынке товаров. Функция спроса на ее продукцию имеет вид Q = 200 – 4P, где: Q – объем продукции (шт.), P – цена продукции (ден. ед.). Производственная функция представлена уравнением Q= 40 + 5L, где Q – объем выпускаемой продукции (шт.), L – количество работников (чел.). Фирма покупает труд на совершенно конкурентном рынке по цене 25 руб. за единицу труда. Фирма максимизирует прибыль. Определите количество используемого труда (L), объем выпуска фирмы (Q) и цену продукции (P).
Тема 9. Рынки капитала и земли

Задача 1. У инвестора есть возможность инвестировать средства в два проекта, которые будут приносить доход на протяжении 3 лет. Согласно расчётам по проектам, по проекту А в первый год инвестор получит 3000 денежных единиц, во второй – 5000 денежных единиц, а в третий год – 4000 денежных единиц, а по проекту Б денежные потоки составят 2000, 1000 и 10000 денежных единиц соответственно. Определите, какой из проектов более выгоден для инвестора при рыночной ставке процента 20% годовых.
Задача 2. Спрос на землю описывается следующим уравнением: Qd=80-2P, где P – цена земли (в 100 тыс. руб. за га), предложение: Qs=40 (га). Определите цену одного гектара земли и земельную ренту, если известно, что ставка банковского процента равна 10. Приведите графическую иллюстрацию решения.
Задача 3.

Спрос на землю описывается следующим уравнением: Qd=140-P, где P – цена земли (в 100 тыс. руб. за га), предложение: Qs=80 (га). Определите цену одного гектара земли и земельную ренту, если известно, что ставка банковского процента равна 10. Приведите графическую иллюстрацию решения.
Задача 4. Спрос на землю равен: Qd=90-P, где P – цена земли в тыс. руб. за га. Площадь земельных угодий равна 20 га.

Определить какие изменения в объеме предложения и цене земли произойдут в результате роста спроса на землю до 1) Qd=130-P, 2) Qd=170-P. Приведите графическую иллюстрацию решения.