СТАТИСТИКА. Стат.Вариант5.. Задача Второй год по сравнению с первым Товар А. цена снизилась на 38. 5% (100 61. 5)
 Скачать 55.75 Kb. Скачать 55.75 Kb.
|
|
Задача 1. По первой группе предприятий 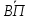 = =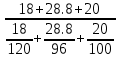 = = 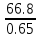 = 102.7% = 102.7%По второй группе 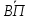 = = 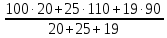 = = 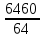 = 100,9% = 100,9%По двум группам  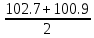 = 101.8% = 101.8%По двум группам предприятий план перевыполняется. Задача 2. Второй год по сравнению с первым Товар А. - цена снизилась на 38.5% (100 – 61.5) - прирост физического объема составил 13.6% (113.6 – 100) ipq=0.615*1.136=0.699 ,т.е. стоимость товарооборота снизилась на 30.1% (100 – 69.9) Товар В. ipq=0.917*0.87=0.797 (себестоимости) (физического объема) (объем в ценах) Третий год по сравнению со вторым. Товар А. Это означает, что цена возросла на 87.5% (187.5 – 100). Прирост физического объема составил 16% (116 – 100). ipq=1.875*1.16=2.175 Товар В. ipq=0.809*1.05=0.85 I = Iq · Iz = 1.063 · 0.949 = 1.009 По товару А произошло снижение цены при увеличении кол-ва продукции, при этом товарооборот снизился. По продукции В цена увеличилась почти в два раза, товарооборот за счет этого увеличился более чем в два раза. Задача 3.
Промышленность = 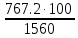 = 49,18%(кредиторская) = 49,18%(кредиторская)Остальные считаем аналогично. Больше всего кредиторской и дебиторской задолженности в промышленной области, меньшая часть в связи. Задача 4. Заданный планом прирост выпуска продукции (18%) выражаем в форме коэффициента роста выпуска продукции в 2019 г. по сравнению с 2018 г.: 1 + 0,18 = 1,18. Фактический процент роста выпуска продукции (113,4%) выражаем в форме коэффициента: 112,3 / 100 = 1,123 ОВВП(%) = 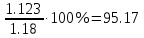 Задача 5. Абсолютный прирост цепной прирост: ∆yц = yi - yi-1 базисный прирост: ∆yб = yi - y1 Темп прироста цепной темп прироста: Tпрцi = ∆yi / yi-1 базисный темп прироста: Tпpб = ∆yбi / y1 Темп роста цепной темп роста: Tpцi = yi / yi-1 базисный темп роста: Tpб = yбi / y1 Абсолютное значение 1% прироста цепной: 1%цi = yi-1 / 100% базисный: 1%б = yб / 100%
Среднее значение ожидаемая продолжительность жизни с 2009 по 2018 составило 70.84 лет Средний темп роста Средний абсолютный прирост. С каждым годом продолжительность жизни увеличивалась на 0.46 лет Задача 6. Находим параметры уравнения методом наименьших квадратов. Система уравнений МНК: an + b∑t + c∑t2 = ∑y a∑t + b∑t2 + c∑t3 = ∑yt a∑t2 + b∑t3 + c∑t4 = ∑yt2
Для наших данных система уравнений имеет вид 13a + 1995b + 336419c = 48.8 1995a + 336419b + 61190505c = 8245.9 336419a + 61190505b + 11812195079c = 1501134.3 Получаем c = -1.1E-5, b = 0.0285, a = -0.335 Уравнение тренда: y = -1.1E-5t2+0.0285t-0.335 Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения тренда к исходным данным. Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерение тесноты зависимости. Изменяется в пределах [0;1]. =  Задача 7. Рассчитаем среднее время обработки одной детали в выборочной совокупности. Все расчёты оформим в таблицу.
мин. Дисперсия выборочной совокупности Средняя ошибка выборки составит 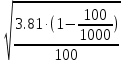 = 0.185 = 0.185С вероятностью 0,997 рассчитаем предельную ошибку выборочной средней. Δ = μ * t t - коэффициент доверия (равен 3) Δ = 0.185 * 3 = 0.555 мин. 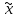 = 24.48 = 24.48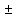 0.55 (мин.) предел, в котором находится среднее время обработки одной детали токарями предприятия. 0.55 (мин.) предел, в котором находится среднее время обработки одной детали токарями предприятия. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
