Работа. Пять задач экономика. Задача1. По заданной функции рыночного спроса 8
 Скачать 79.4 Kb. Скачать 79.4 Kb.
|
|
Тема №1 Вычисление показателей эластичность функции Задача№1. По заданной функции рыночного спроса 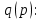 8. 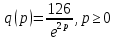 а) задайте аналитически 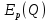 , показывающую точечную эластичность спроса по цене p; , показывающую точечную эластичность спроса по цене p;б) нарисуйте в системе координат p-q кривую спроса и график функции 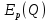 ; ;в) определите, при каких ценах спрос эластичен. Решение: Эластичностью функции 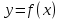 называется предел соотношения относительных изменений переменных y и x. Если эластичность переменной y при изменении переменной x обозначим через называется предел соотношения относительных изменений переменных y и x. Если эластичность переменной y при изменении переменной x обозначим через 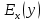 , то используя определения производной получаем: , то используя определения производной получаем: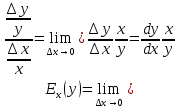 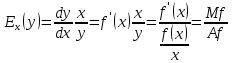 Где Mf- предельное значение функции в точке x, а Af- среднее значение функции в точке x. Отметим, что эластичность функции характеризуется непосредственно коэффициентом эластичности. Коэффициент эластичности – это числовой показатель, показывающий процентное изменение одной переменной в результате однопроцентного изменения другой переменной. Чтобы найти аналитическое выражение 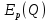 для данной задачи, находим, что для данной задачи, находим, что 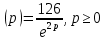 , т.е. область определения функции спроса. , т.е. область определения функции спроса.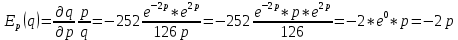 В системе координат (p-q)рисуем график функции 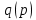 и и 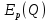 : : P P    2 2 Ep(q) q(p)          -4 0 2,31 q Спрос эластичен, если 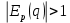 , т.е. , т.е. 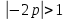 , , 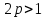 , , 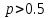 . Следовательно, спрос эластичен в интервале . Следовательно, спрос эластичен в интервале 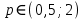 Тема №2 Модели межотраслевого баланса Задача №2. В таблице приведены коэффициенты прямых затрат 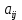 и конечная продукция отраслей и конечная продукция отраслей 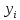 на плановый период, усл. ден.ед. на плановый период, усл. ден.ед.
Найти: 1. Плановые объемы валовой продукции отраслей 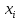 , межотраслевые поставки , межотраслевые поставки 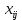 , чистую продукцию отраслей , чистую продукцию отраслей 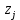 ; ;2. необходимый объем валового выпуска каждой отрасли 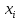 , если конечное потребление продукции сельского хозяйства увеличится на 25%, а промышленности на 20%. , если конечное потребление продукции сельского хозяйства увеличится на 25%, а промышленности на 20%.Решение: I. а) Найдем плановые объемы валовой продукции отраслей 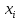 по формуле: по формуле: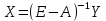 зная, что задана матрица прямых затрат: 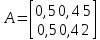 и вектор конечного продукта: 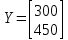 Из курса высшей математики известно, что обратная матрица 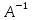 к матрице к матрице 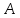 вычисляется по следующей формуле: вычисляется по следующей формуле: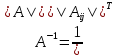 где: 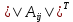 – транспонированная матрица, элементами которой является алгебраическое дополнение. – транспонированная матрица, элементами которой является алгебраическое дополнение.В общем случае, алгебраическим дополнением элемента 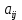 квадратной матрицы квадратной матрицы 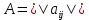 , называется минор (n-1)-го порядка, который получается из матрицы , называется минор (n-1)-го порядка, который получается из матрицы 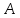 вычеркиванием элементов ее i-й строки и j-го столбца, умноженный на вычеркиванием элементов ее i-й строки и j-го столбца, умноженный на 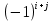 , т.е. , т.е.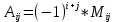 где: 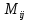 - минор (n-1)-го порядка. - минор (n-1)-го порядка.Тогда обратная матрица 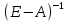 к матрице к матрице 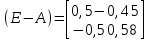 вычисляется следующим образом: 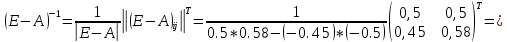 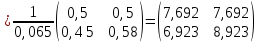 Тогда 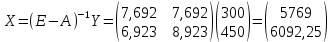 т.е. 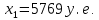 , , 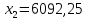 у.е. у.е.б) Найдем межотраслевые поставки 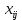 . Коэффициент прямых затрат определяется как объём ресурса . Коэффициент прямых затрат определяется как объём ресурса 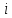 , необходимый для производства единицы продукта , необходимый для производства единицы продукта 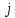 , т.е. , т.е. 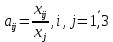 Отсюда можно найти 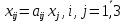 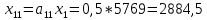 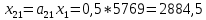 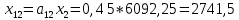 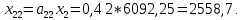 в) Найдем условно чистую продукцию 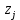 . .Условно чистая продукция вычисляется по следующей формуле: 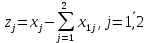 Отсюда 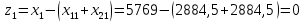 и 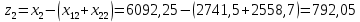 II. Если конечное потребление продукции сельского хозяйства увеличится на 25%, а промышленности на 20%, тонеобходимый объем валового выпуска каждой отрасли 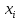 вычисляется следующим образом: вычисляется следующим образом: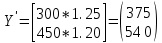 Тогда валовый выпуск будет равен 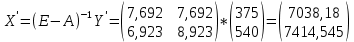 т.е. 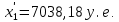 , , 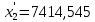 у.е. у.е.Тема №3 Модели экономического роста (модель Солоу) Задача 3. В момент времени 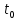 в экономике имеется в экономике имеется 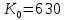 единиц капитала и единиц капитала и 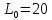 единиц труда. Условия производства представлены производственной функцией единиц труда. Условия производства представлены производственной функцией 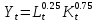 . Темп прироста трудовых ресурсов равен 3% за период. Население сберегает 22% национального дохода, норма выбытия равна 7% в год. Как изменится средняя производительность труда в периоде . Темп прироста трудовых ресурсов равен 3% за период. Население сберегает 22% национального дохода, норма выбытия равна 7% в год. Как изменится средняя производительность труда в периоде 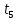 по сравнению с периодом по сравнению с периодом 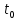 ? ?Решение: 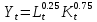 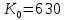 , , 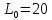 Y – ВВП, X=C+I C-потребление, I-инвестиция. 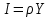 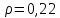 или 22% - норма сбережения; или 22% - норма сбережения;Тогда 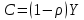 За время 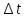 ресурсы каптала изменится следующим образом: ресурсы каптала изменится следующим образом: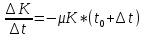 где: 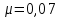 или 7% - норма выбытия. или 7% - норма выбытия.Чтобы обеспечит необходимый уровень производительности, ресурсы капитала обновляются, т.е. за это же время 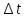 инвестируется капитал в размере инвестируется капитал в размере 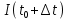 : :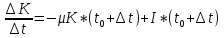 . .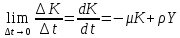 Темп прироста за это же время 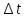 состовляет: состовляет: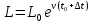 где: 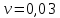 или 3% - темп прироста трудовых ресурсов (или населения). или 3% - темп прироста трудовых ресурсов (или населения).А производительности труда по объему выпуска: 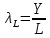 Полученные уравнения запишем в виде одной системы: 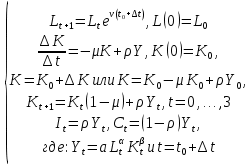 Эта система называется модель экономического роста или модель Солоу. Используя этой системы заполняем следующую таблицу:
Итак производительности труда в периоде 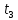 по сравнению с периодом по сравнению с периодом 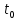 снизился в снизился в абсолютном выражении на величину 13,27 – 10,4 = 2,87 или в относительном выражении 2,87 / 13,27 = 0,21628 (21,628%) Тема №4 Золотое правило накопления Задача 4. Рассматривается производственный процесс, описываемой производственной функцией 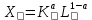 . Доля дохода капитала в общем доходе составляет . Доля дохода капитала в общем доходе составляет 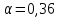 , темп прироста численность населения равен , темп прироста численность населения равен 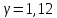 % в год, а норма амортизации капитала составляет % в год, а норма амортизации капитала составляет 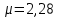 % в год. Определит норму сбережения (накопления) % в год. Определит норму сбережения (накопления) 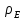 , капиталовооруженность эффективного труда , капиталовооруженность эффективного труда 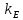 и максимальное потребление на душу населения и максимальное потребление на душу населения 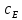 соответствующие золотому правилу. соответствующие золотому правилу.Решение: Отметим, что стационарный режим (траектория сбалансированного роста), в котором потребление 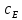 максимально, называют “золотым правилом”, т.е. правило деления выпуска на потребление и накопление, обеспечивающее максимальное стационарное потребление, называется “золотым”. С другой стороны, нам известно, что основное уравнение динамики роста экономики в модели Солоу на душу населения имеет следующий вид: максимально, называют “золотым правилом”, т.е. правило деления выпуска на потребление и накопление, обеспечивающее максимальное стационарное потребление, называется “золотым”. С другой стороны, нам известно, что основное уравнение динамики роста экономики в модели Солоу на душу населения имеет следующий вид: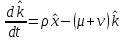 где: 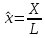 – ВВП (внутренняя валовая продукция) на душу населения; – ВВП (внутренняя валовая продукция) на душу населения; 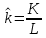 – капиталовооруженность (фондовооруженность) эффективного труда – сколько фондов на одного рабочего; – капиталовооруженность (фондовооруженность) эффективного труда – сколько фондов на одного рабочего; 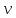 - темп прироста числа занятых (пропорционально численность населения); - темп прироста числа занятых (пропорционально численность населения); 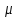 – коэффициент выбытия основного фонда (темп прироста эффективности труда). – коэффициент выбытия основного фонда (темп прироста эффективности труда).Для заданной производственной функции Кобба-Дугласа 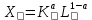 имеем: 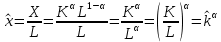 Тогда основное уравнение динамики роста экономики принимает следующий вид: 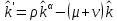 а уравнение потребления на душу населения: 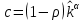 Из уравнения потребления видно, чтобы увеличить значение потребление на душу населения нужно уменьшит 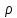 и увеличить и увеличить 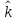 . Таким образом, наша задача подбирать такое . Таким образом, наша задача подбирать такое 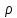 , при котором , при котором 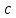 достигает своего максимального значения на траектории сбалансированного роста, т.е. при достигает своего максимального значения на траектории сбалансированного роста, т.е. при 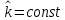 . Тогда, на траектории сбалансированного роста . Тогда, на траектории сбалансированного роста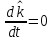 или 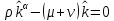 Отсюда, капиталовооруженность эффективного труда на траектории сбалансированного роста 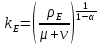 и потребление 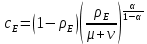 Чтобы определить норму сбережений 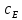 , соответствующую золотому правилу (см. определения) подбираем такой , соответствующую золотому правилу (см. определения) подбираем такой 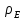 при котором при котором 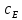 максимален, т.е. найдем максимум функции максимален, т.е. найдем максимум функции 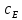 по по 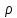 : :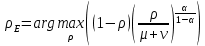 Для этого из уравнения, относительно 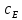 берем производной по берем производной по 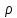 и приравниваем к нулю: и приравниваем к нулю: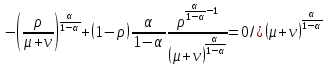 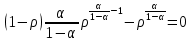 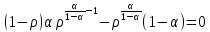 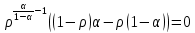 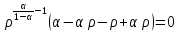 Отсюда 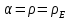 Таким образом: 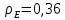 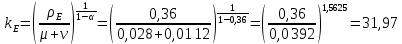 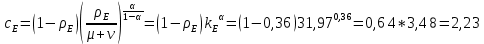 у.е. у.е.Тема №5 Задачи максимизации потребительского выбора Задача 5. Пусть функция полезности задана с помощью производственной функциейКобба – Дугласа 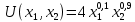 . Цены на товары . Цены на товары 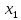 и и 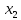 равны равны 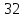 и и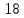 усл.ед. соответственно. Бюджет потребителя составляет усл.ед. соответственно. Бюджет потребителя составляет 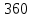 усл.ед. Определить набор товаров потребителя усл.ед. Определить набор товаров потребителя 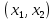 максимизирующий функцию полезности максимизирующий функцию полезности 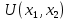 . .Решение: В общем случае задачи максимизации потребительского выбора ставится следующим образом: 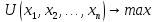 (1) (1)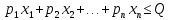 (2) (2)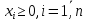 (3) (3)Решение задач условной оптимизации (1)-(3) осуществляется методом множителей Лагранжа. Для этого строиться функции Лагранжа 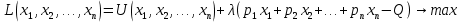 и находятся ее первые частные производные по 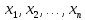 и и 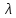 и приравниваются к нулю: и приравниваются к нулю: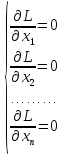 или или 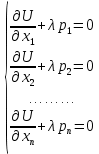 (4) (4)Далее из полученной системы (4) выразим значения векторов 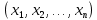 , являющиеся критической точкой функции Лагранжа. , являющиеся критической точкой функции Лагранжа.Относительно нашей задачи метод Лагранжа принимает следующий вид: 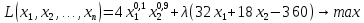 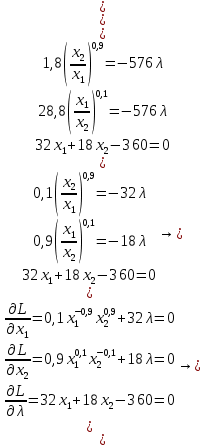 Отсюда приравниваем левые части двух первых уравнений, получим: 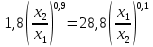 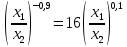 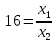 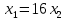 Подставляя в третье уравнение получаем: 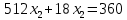 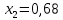 Тогда 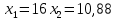 . Таким образом, точка . Таким образом, точка 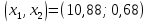 является решением задачи потребительского выбора. Значение функции полезности, соответствующее этому набору, составляет: является решением задачи потребительского выбора. Значение функции полезности, соответствующее этому набору, составляет: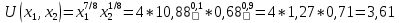 . .Отметим, что в общем случае, каждый потребитель имеет свою функцию полезности. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

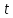
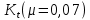
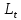
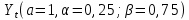
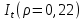
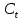
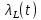 =
=