Контрольная по Ким. контрольная работа и метапредмет (3). Задачами, Пространственные отношения. Геометрические фигуры, Геометрические величины
 Скачать 74.11 Kb. Скачать 74.11 Kb.
|
|
Требования к современным КИМам* Представленность в работе заданий из всех разделов начального курса математики: «Числа и величины», «Арифметические действия», «Работа с текстовыми задачами», «Пространственные отношения. Геометрические фигуры», «Геометрические величины», «Работа с информацией». Заметим, что выполнение заданий может быть связано с проявлением умений как из одного раздела курса математики (вычисли начение выражения, сравни числа, отметь на чертеже все прямые углы, подбери вопросы, подходящие к условию задачи), так и из разных разделов (Вычисли значения выражений и расположи числа-результаты в порядке возрастания – «Арифметические действия» и «Числа и величины», Вычисли площадь прямоугольника с заданными длинами сторон – «Геометрические фигуры», «Геометрические величины», «Арифметические действия», Реши задачу – «Текстовые задачи», «Арифметические действия»). Наличие заданий двух уровней сложности – базового и повышенного. Задания базового уровня сложности – стандартные задачи, в которых очевиден (алгоритмизирован) способ решения, например: вычисли значение суммы, построй прямоугольник с длинами сторон 4 см, 6 см и вычисли его площадь и периметр. Повышенный уровень сложности составляют задания, в которых нет явного указания на способ выполнения, и ученику приходится самостоятельно выбирать один из изученных способов или создавать новый способ, возможно, интегрируя знания из разных предметных областей (например: продолжи закономерность, зачеркни «лишнюю фигуру»). Задания и базового и повышенного уровня сложности разрабатываются на материале раздела в перечне планируемых результатов «Ученик научится». Операционализация (пооперационный контроль). Суть этого требования: ученик решил уравнение неправильно. Свидетельствует ли это о том, что у него не сформировано умение решать уравнения? Разумеется, нет. Необходимо выяснить причину ошибки – возможно, ученик допустил погрешность в вычислениях, что характеризует несформированность у него умений в этой области математического знания (а не в решении уравнений). Поэтому нужны такие измерители, которые позволят установить место затруднения у ученика, выявить ту операцию (умение), которая нарушена. Это позволит педагогу своевременно проводить коррекционные мероприятия, направленные на конкретное затруднение. В этой связи в каждой содержательной линии курса начальной математики выделены предметные результаты, состоящие из конкретных умений (операций) – Приложение 1. Контрольно-измерительные материалы должны содержать задания, проверяющие конкретные выделенные умения. Преобладание в работе практико-ориентированных заданий (для диагностики сформированности у учащихся представлений о математике как науке, описывающей процессы и закономерности, происходящие в окружающем мире, а также способности использовать знания для исследования математической сущности объекта, предмета или явления). В связи с потребностью современного общества у учащихся должна быть сформирована система жизненно важных практических умений, а не разрозненные знания из разных предметных областей, поэтому учебные задания модифицируются, в том числе и контрольно-измерительные, – приоритет имеют практико-ориентированные задания, при решении которых учащиеся переносят теоретические знания в конкретную жизненную ситуацию (например, вычисляют не периметр прямоугольника, а длину забора, ограждающего участок земли прямоугольной формы). Наличие в одной проверочной (контрольной) работе заданий разного типа (по условиям нахождения и записи ответа). Это задания с выбором одного верного ответа (из четырех предложенных вариантов), задания с выбором всех верных ответов – от двух до пяти (из шести предложенных вариантов), задания на установление соответствия, задания с кратким ответом (требуется вписать слово, число, знак действия и т.п.), задание с развернутым ответом (запись решения примера, задачи, уравнения, обоснование своей точки зрения). Возможность измерения не только предметных, но и некоторых метапредметных результатов обучения. К предметным результатам относятся группы умений (операций) по каждому разделу начального курса математики. Метапредметные результаты обучения – это сформированные универсальные учебные действия (познавательные, коммуникативные, регулятивные или организационно-рефлексивные); для таких умений характерна универсальность и способность переноса в любую сферу деятельности. Критериальное оценивание. Оценивание является одним из основных звеньев в образовательном процессе. Оценка должна основываться на критериях, предъявляемых к работе, и из них же следовать. При этом критерии должны быть понятны как учителю, так и ученикам, четко сформулированы и разработаны для каждой контрольной работы (разработка критериев к контрольным работам может быть совместной деятельностью учителя и учащихся). Соблюдение этих требований позволит сделать оценку «прозрачной» и более объективной. Задание 1. Установите соответствие (несоответствие) контрольной работы требованиям к современным КИМам*. 1. Толя записал число тридцать тысяч восемнадцать. Какое число записал Толя? А) 3000018 В) 30018 Б) 300018 Г) 3018 2. Саша сложил из двух одинаковых открыток квадратной формы прямоугольник.  8 см Его периметр равен: А) 24 см Б) 64 см В) 48 см Г) 8 см 3. Выполняя задание: «К частному чисел 171 и 3 прибавить произведение чисел 75 и 5» учащиеся записали разные выражения. Кто из учеников прав? А) Петя (171 – 3) + 75 ∙ 5 Г) Лена (171 : 3) + 75 ∙ 5 Б) Саша 171 ∙ 3 + 75 : 5 Д) Егор 171 : 3 + (75 – 5) В) Катя 171 : 3 + 75 ∙ 5 Е) Вова 171 : 3 + (75 + 5) 4. Жители Солнечного города Винтик, Шпунтик и Незнайка играли в «сказочное» домино, используя фигурки:      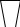 1 2 4 5 6 3 Какие из этих фигурок имеют более двух прямых углов? А) 1, 3, 4, В) 1, 5, 6 Б) 1, 6 Г) 2, 3, 4 5. Миша отмечает в календаре дни февраля, когда он посещает бассейн: 1, 5, 10, 16, ... Определи закономерность и продолжи числовой ряд. Запиши ответ. Ответ: _______________________________. 6. Не выполняя арифметическое действие, поставь знак сравнения: 385 + ð = 869 5 869 – ð = 915 + 34 384 + ∆ = 869 5 869 – ∆ = 915 – 34 ð___∆ ð___∆ Ответ: _______________________________. 7  . Число лучей на чертеже равно . Число лучей на чертеже равно М Р А) 0 В) 2 Б) 4 Г) 5 8. Длина какой ломаной равна длине отрезка АВ? 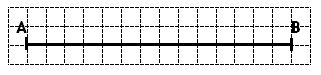 А   ) Б) ) Б)   В) Г) В) Г) 9. Поезд Пермь – Адлер идет ровно 72 часа. Во сколько часов, и какого числа поезд вышел из Перми, если он прибыл в Адлер 28 июня в 6 часов вечера? Дополнительная информация: когда в Перми полдень, в Адлере 10 часов утра. Запиши ответ. Ответ: __________________________________. 10. Итоги спортивных соревнований по прыжкам в длину с разбега были занесены в таблицу.
Если норма длины прыжка с разбега не менее 180 см, то ее выполнили: А) 7 учащихся В) 10 учащихся Б) 9 учащихся Г) 20 учащихся 11. Папа измерил высоту окна и получил число 13. Какую единицу измерения использовал папа? А) 1 дм Б) 1 см В) 1 м Г) 1 кг 12. Туристы осматривали здание музея. Если посмотреть на него сверху, снизу, сбоку, спереди и сзади, то видно квадрат. Какую форму имеет здание музея. Запиши ответ. Ответ: ____________________. Ответ: _____________________. 13. Учитель записал на доске числа 31, 53, 97, 75, 42. Что общего у этих чисел? Допиши недостающие числа, обладающие этим же свойством. Ответ: ___________________________. 14. Внимательно прочитай задачу: «В магазин привезли 11 мешков с мукой высшего сорта и 8 мешков с мукой грубого помола. Сколько килограммов муки привезли в магазин, если мешок муки высшего сорта весит 15 кг, а мешок муки грубого помола 22 кг?» Петя решил задачу так: 1) 15 ∙ 11 = 165 2) 165 + 176 = 341 Настя сразу заметила, что в этом решении одно действие пропущено. Отметь и ты пропущенное действие: А) 11∙ 16 = 176 В) 22 ∙ 8 = 176 Б) 341 – 165 = 176 Г) 165 + 11 = 176 15. В сказочной стране числа записывают при помощи волшебных цифр. Числовая последовательность выглядит так: ▲, O, ■, ☼, ♦, ♥, ◘, ●, ▬, ☺, O▲, OO, … Реши примеры: А) ■☼♥ Б) ☺◘▬ + ◘♦ – ☼O♥
26. На участке прямоугольной формы посажены 24 яблони по 1 яблоне на квадратный метр. Чему может быть равна длина забора, ограждающего данный участок? Найди разные варианты решения и объясни ответ.
Задание 2. Заполните столбики рефлексивной таблицы, свободные от текста.
Задание 3. В каждом задании выделите предметный и метапредметный образовательный результат. 1 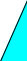 . Отметь лишнюю фигуру . Отметь лишнюю фигуруа    ) б) в) г) ) б) в) г) Предметный результат________________________________________________ Метапредметный результат______________________________________________ 2. Ученики составляли задачи на правило (Ω + €) : J = Ω : J + € : J. Кто справился с заданием? Отметь. а) Соня: «На изготовление одного венка нужно 15 лютиков и 30 ромашек. Надя сплела 3 венка. Сколько цветов ей потребовалось?» б) Лена: «Для выполнения проекта по математике 13 девочек и 15 мальчиков ученики класса распределились в группы по 4 человека. Сколько групп получилось?» в) Рая: «Размах крыльев стрекозы 18 см, бабочки – на 12 см больше, чем стрекозы. Размах крыльев бабочки в 5 раз меньше, чем аиста. Чему равен размах крыльев аиста? г) Вита: «12 окуньков и 16 ершей разложили в 4 кошачьи миски поровну. Сколько окуньков и ершей в одной миске?» д) Вася: «Мама купила 8 яблок и 12 груш. Четверть всех фруктов съели. Сколько фруктов осталось? е) Коля: «Для украшения зала Маша вырезала 20 снежинок и 16 флажков. Половиной фигур украсили зал, остальные повесили на ёлку. Сколько фигур на ёлке?» Предметный результат______________________________________________________ Метапредметный результат______________________________________________ 3. Ученикам нужно было записать ряд из пяти различных двузначных чисел: первое и последнее числа должны быть чётные, последнее – меньше 15, второе больше третьего, четвёртое не 23. Кто из учеников правильно выполнил задание? Отметь. а) Лиза: 32, 65, 54, 87, 12; б) Влад: 60, 78, 14, 32, 12; в) Максим: 12, 16, 15, 35, 12; г) Наташа: 68, 11, 10, 45, 14; д) Яна: 4, 67, 43, 23, 35; е) Ира: 44, 78, 68,14. Предметный результат________________________________________________ Метапредметный результат______________________________________________ 4. Отметь задания, которыми не справится ученик, если он знает, что 1 сантиметр меньше 1 метра, но забыл на сколько меньше: А) сравни 3 м и 3 см Б) сравни 3 км 518 м и 3615 м В) 1 м – 1 см Г) 3 м 15 см – 2 м 12 см Д) 3 м 5 см + 604 см Е) сравни 325 см и 3 м Предметный результат________________________________________________ Метапредметный результат______________________________________________ 5. В сказочной стране все цифры, кроме нуля, обозначаются знаками, отличными от привычных нам изображений. Но сохраняется правило: «Одинаковые цифры обозначаются одинаковыми знаками, разные цифры – разными знаками». Отметь выражения, значения которых можно вычислить таким способом: ▲♦ ∙ ▲ = (▲0 + ♦) ∙▲ = ▲0 ∙ ▲ + ♦ ∙ ▲ А) 40 ∙ 4 Б) 43 ∙ 3 В) 86 ∙ 4 Г) 48 ∙ 4 Д) 23 ∙ 2 Е) 123 ∙ 2 Предметный результат________________________________________________ Метапредметный результат______________________________________________ 6. Отметь лишнее выражение А) 13 □ 4 + 13 □ 7 Б) 13 □ 9 + 13 □ 2 В) 13 □ 10 + 13 Г) 13 □ 10 + 10 Предметный результат________________________________________________ Метапредметный результат______________________________________________ 7. Выполни задания, пользуясь содержанием энциклопедии «111 страниц о деревьях-долгожителях». Обрати внимание, что каждая статья начинается с новой страницы! На страницах, номера которых заканчиваются цифрой 4 (4, 14 и т. д.), помещены фотографии – по четыре на странице. Рисунок: страничка энциклопедии с надписью «Содержание» Баньян……………………………………………3 Баобаб ……………………………………….....19 Драконово дерево ……………………………..36 Дуб обыкновенный ……………………………59 Ель обыкновенная ……………………………..75 Секвойя………………………………….. ……. 86 Сосна…………………………………………….98 На какой странице заканчивается статья о баобабе? _______________ Сколько всего страниц в энциклопедии?________________ Сколько всего фотографий в энциклопедии?________________ Сколько фотографий посвящено баньяну?__________ Сколько страниц текста без фотографий посвящено сосне?________ На сколько страниц больше самая длинная статья, чем самая короткая? ________ Предметный результат________________________________________________ Метапредметный результат______________________________________________ 8. Прочитай рассказ Риты о своей семье: «Мне 8 лет. Самая старшая в нашей семье – бабушка, ей 68 лет. Дедушка младше бабушки на 2 года. Моя сестра Лена в 2 раза старше меня, а мой брат Денис в 2 раза младше меня. Когда родился папа, дедушке было 25 лет. Мама младше папы на 3 года». На эти вопросы можно ответить, не выполняя арифметических действий. а) Сколько лет маме? б) Сколько детей в семье? в) Кто старше: Лена или Данил? г) Во сколько раз Рита старше Данила? д) На сколько лет Рита старше Данила? е) На сколько лет дедушка старше папы? Предметный результат________________________________________________ Метапредметный результат______________________________________________ Задание 4. Спроектируйте задания с метапредметным компонентом на заданные предметные умения.
Приложение 1 Предметные результаты по математике
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
