Doolin_V_V_203501_Omsk_2k_1sem_Fizika_2_KR_нз_2021.11.20. Задачи 21, 41 не зачтены. Работа в целом не зачтена
 Скачать 239.88 Kb. Скачать 239.88 Kb.
|
|
Задачи 21, 41 не зачтены. Работа в целом не зачтена. Если работа в целом не зачтена, то для зачета необходимо 6 полностью зачтенных задач. Должны быть представлены все задачи. Мои замечания и вопросы, и свои записи, к которым они были сделаны, не стирать. Отвечайте сразу после вопроса, но ответ записывайте другим, например, синим, цветом и быстрее высылайте файл с исправлениями. 20.11.2021 Федеральное агентство железнодорожного транспорта федеральное государственное бюджетное образовательное учреждение высшего образования «Омский государственный университет путей сообщения» (ОмГУПС (ОмИИТ)) Кафедра «Физика и химия» Контрольная работа - 2 Вариант -1 Выполнил: ст. гр ОД -203501 Дулин В.В. Проверил: Доцент, к.ф.-м.н. Сосновский Юрий Михайлович Омск 2021 г. Задача 1. Электрическое поле образовано бесконечной плоскостью, заряженной с поверхностной плотностью 1,40 мкКл/м2, и двумя точечными зарядами 20,0 и –40,0 нКл. Заряды расположены на одной прямой, параллельной плоскости, на расстоянии 160 мм друг от друга. Найти значение и направление напряженности электрического поля в середине этого расстояния. Дано: СИ   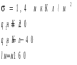 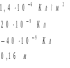 ------------------------------------------------- 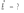 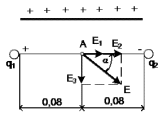 Решение. Электрическое поле создается тремя заряженными телами: положительным точечным зарядом  , отрицательным точечным зарядом , отрицательным точечным зарядом  и бесконечной плоскостью. Определяем направление векторов напряженности электрического поля, созданного плоскостью: вектор и бесконечной плоскостью. Определяем направление векторов напряженности электрического поля, созданного плоскостью: вектор  направлен перпендикулярно плоскости, «отвернувшись» от положительно заряженной плоскости; и точечными зарядами: вектор направлен перпендикулярно плоскости, «отвернувшись» от положительно заряженной плоскости; и точечными зарядами: вектор 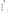 направлен вдоль прямой, соединяющий точку А и заряд q1, «отвернувшись» от положительного заряда q1 и вектор направлен вдоль прямой, соединяющий точку А и заряд q1, «отвернувшись» от положительного заряда q1 и вектор 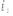 направлен вдоль прямой, соединяющий точку А и заряд q2, «повернувшись» к отрицательному заряду q2. Результирующую напряженность направлен вдоль прямой, соединяющий точку А и заряд q2, «повернувшись» к отрицательному заряду q2. Результирующую напряженность 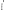 в точке А найдем по принципу суперпозиции электрических полей: в точке А найдем по принципу суперпозиции электрических полей: 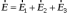 . .Для записи этого векторного уравнения в скалярной форме выбираем инерциальную систему отсчета и находим проекции всех векторов на координатные оси: 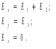  Величину напряженностей полей, создаваемых каждым электрическим зарядом, вычисляем по формулам: – для бесконечной заряженной плоскости 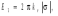 где 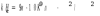 – электрическая постоянная. – электрическая постоянная.– для точечного электрического заряда 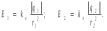 где 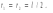 Тогда Тогда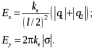 Проверяем единицы измерения:  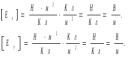 Производим вычисления: 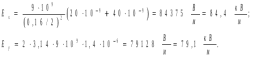 Величину напряженности в точке А найдем по формуле  Определяем направление напряженности Е 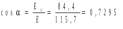 , откуда , откуда 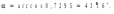 Ответ: 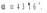 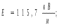 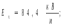 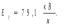 Задача 11. Энергия плоского воздушного конденсатора 0,42 нДж, разность потенциалов на обкладках 60 В, площадь пластины 1,2 см2 . Определить расстояние между обкладками, напряженность и объемную плотность энергии электрического поля внутри конденсатора. 
Решение: Из формулы нахождения энергии плоского воздушного конденсатора находим электроемкость: 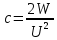 по определению электроемкость равна: 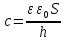 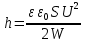 ε0=8.85*10-12 Ф/м h = 0,0045 м напряженность конденсатора равна: E =U/h E = 13333 В/м Объемная плотность конденсатора равна: 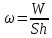 ω = 0,00077 Ответ: h = 0.0045 м E = 13333 В/м ω = 0,00077 Задача 21. В схеме E1 и E2 два элемента с одинаковым внутренним сопротивлением, равным 0,50 Ом (E1 = 2,00 В; E2 = 3,00 В). Найти силу тока, текущего: 1) через сопротивление R1 = 0,50 Ом; 2) через сопротивление R2 = 1,50 Ом; 3) через элемент E1.
Ответ: I1=1,12 A ; I=2,88 A; I2 = 1,78 A Задача не зачтена. Задача 31. Электрон с кинетической энергией 4,00 кэВ попадает в магнитное поле с индукцией 10,0 мТл перпендикулярно его линиям. Найти радиус кривизны траектории электрона в магнитном поле. 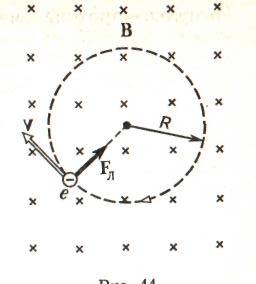   Дано: СИ Дано: СИ 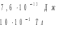 -------------------------------------- 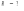 Решение. Радиус кривизны траектории электрона определим, исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца 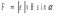 , где F – сила Лоренца, , где F – сила Лоренца, 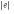 – модуль заряда электрона, v – скорость электрона, В – магнитная индукция, – модуль заряда электрона, v – скорость электрона, В – магнитная индукция, 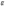 – угол между направлением тока и вектором магнитной индукции – угол между направлением тока и вектором магнитной индукции  . В нашем случае . В нашем случае 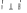 и и 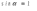 , тогда , тогда 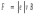 . Направление силы Лоренца определяется по правилу левой руки: если ладонь левой руки расположить так, чтобы магнитные линии входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (против направления движения отрицательного заряда, например, электрона), то большой палец, отставленный на 90 , покажет направление силы Лоренца (рис. а и б). . Направление силы Лоренца определяется по правилу левой руки: если ладонь левой руки расположить так, чтобы магнитные линии входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (против направления движения отрицательного заряда, например, электрона), то большой палец, отставленный на 90 , покажет направление силы Лоренца (рис. а и б). Вектор силы Лоренца перпендикулярен вектору скорости и, следовательно, по второму закону Ньютона, сообщает электрону нормальное ускорение 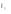 : : 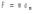 , где F – сила Лоренца, т – масса электрона, , где F – сила Лоренца, т – масса электрона, 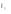 – нормальное ускорение. Так как нормальное ускорение – нормальное ускорение. Так как нормальное ускорение 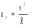 , то , то  . Отсюда находим радиус окружности: . Отсюда находим радиус окружности: 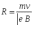 . Входящий в выражение импульс . Входящий в выражение импульс 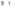 выразим через кинетическую энергию Т электрона: выразим через кинетическую энергию Т электрона: 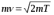 . .Окончательно 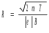 . .Проверим единицу измерения: 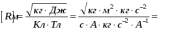 . .Производим вычисления: 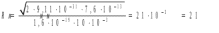 . .Ответ. 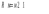 . .Задача 41. В однородном магнитном поле, индукция которого равна 0,08 Тл, вращается катушка, содержащая 400 витков. Период обращения катушки равен 3,00 с, площадь ее поперечного сечения составляет 6,00 см2. Определить максимальное значение ЭДС индукции во вращающейся катушке и ЭДС индукции через 0,25 с после начала вращения. Первоначально плоскость витков катушки была перпендикулярна магнитному полю. Дано: СИ   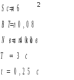  -----------------------------------------  Решение. Мгновенное значение ЭДС индукции 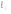 определяется основным уравнением электромагнитной индукции Фарадея-Максвелла: определяется основным уравнением электромагнитной индукции Фарадея-Максвелла: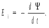 (1) (1)Потокосцепление 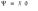 , где , где 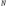 – число витков катушки, пронизываемых магнитным потоком Ф. Подставив выражение – число витков катушки, пронизываемых магнитным потоком Ф. Подставив выражение 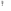 в формулу (1), получим в формулу (1), получим 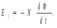 (2) (2)При вращении катушки магнитный поток Ф, пронизывающий катушку в момент времени 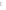 , изменяется по закону , изменяется по закону 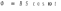 , , Как получена эта формула? Поясните подробно. где 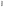 – магнитная индукция; – магнитная индукция; 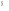 – площадь катушки; – площадь катушки; 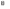 – угловая скорость катушки. Подставив в формулу (2) выражение магнитного потока Ф и продифференцировав по времени, найдем мгновенное значение ЭДС индукции: – угловая скорость катушки. Подставив в формулу (2) выражение магнитного потока Ф и продифференцировав по времени, найдем мгновенное значение ЭДС индукции: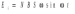 . .Заметив, что угловая скорость 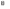 связана периодом обращения связана периодом обращения 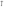 катушки соотношением катушки соотношением 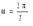 , получим , получим 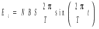 Проверим единицу измерения: 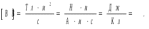 Максимальное значение ЭДС при  , поэтому , поэтому 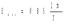 . .Производим вычисления: 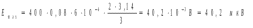 Мгновенное значение ЭДС индукции в момент времени 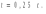 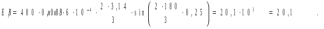 Ответ. 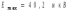 . .  Задача не зачтена. Задача 51. Материальная точка массой 5 г совершает гармонические колебания по закону синуса с циклической частотой 0,5 с-1 , амплитудой 3 см и нулевой начальной фазой. Определить скорость точки в момент времени, когда ее смещение равно 1,5 см и положительно; максимальную силу, действующую на точку; полную энергию колеблющейся точки.   Дано: СИ Дано: СИ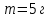 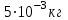 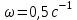 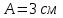 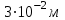 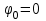  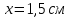 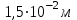 Определить 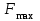 ; ; 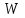 . .Решение Уравнение гармонических колебаний имеет вид 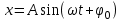 или или 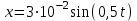 . .Скорость точки 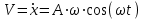 . .Время t находим из условия, что 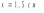 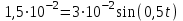 , откуда , откуда 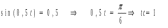 . .Тогда скорость точки 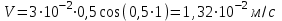 . .Максимальную силу найдем по формуле 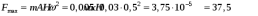 . .Полная энергия колеблющейся точки 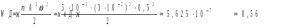 . . Ответ. 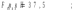  |