Геометрия. Задачи на построение
 Скачать 144.83 Kb. Скачать 144.83 Kb.
|
|
Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 12 муниципального образования Усть – Лабинский район РАЗРАБОТКА УРОКА ПО ГЕОМЕТРИИ 7 КЛАСС. Тема: «Задачи на построение». Разработала Науменко А.А., учитель математики МБОУ СОШ № 12 2015 Услышишь - забудешь, Увидишь - запомнишь, Построишь - поймёшь. Конфуций Тема. Задачи на построение. Цели урока: образовательные: дать представление о задачах на построение с использованием циркуля и линейки без делений; рассмотреть простейшие задачи на построение обучать созданию математических моделей. развивающие: развитие навыков умственного труда: алгоритма деятельности, решение проблемной задачи, развитие алгоритмического, логического, творческого мышления; формирование навыков исследовательской, творческой деятельности при решении задач на построение. воспитательные: воспитывать ответственное отношение к труду воспитывать волю и настойчивость для достижения конечных результатов Тип урока: урок ознакомления с новым материалом, урок моделирования способов решения проблемных задач Оборудование: мультимедийное оборудование, раздаточный материал (тесты на повторение, заготовки для решения творческих задач), ХОД УРОКА Организационный момент. Французский писатель Анатоль Франц заметил, что: «Учиться можно только весело. Чтобы переваривать эти знания, нужно поглощать эти знания с аппетитом». Давайте сегодня на уроке будем следовать этому совету. Будем активны, будем поглощать знания с большим желанием, потому что они пригодятся вам в дальнейшей жизни. Желаю вам успехов в работе. 1) Повторение по теме « Геометрические фигуры». На экране изображены фигуры (точки, прямые, лучи, отрезок, углы, окружность, треугольники), карточки с такими же задания лежат на столе у учащихся. Учащимся предлагается назвать их, дать им определение, назвать их элементы, показать варианты их обозначения. При необходимости учитель может задавать наводящие вопросы. - Что представляет собой множество всех точек, удалённых от данной точки на данное расстояние? - Что такое центр, радиус, хорда, диаметр, дуга окружности? - Назовите самую большую хорду в окружности? - Что называется: точкой, прямой, лучом, углом, треугольником? 2). Повторение темы «Признаки равенства треугольников» по слайдам на доске. Учащиеся называют три признака равенства треугольников, которые появляются на экране по мере их озвучивании. Первый признак равенства треугольников - по двум сторонам и углу между ними. 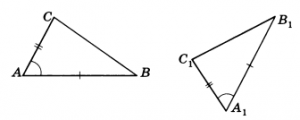 Второй признак равенства треугольников – по стороне и двум прилежащим углам. 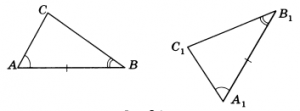 Третий признак равенства треугольников – по трем сторонам. 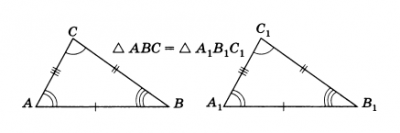 Изучение нового материала. Вводное слово учителя. Геометрические задачи на построение, возможно, самые древние математические задачи. Задачи на построение способствуют пониманию происхождения различных геометрических фигур, возможности их преобразования Они развивают логическое мышление, геометрическую интуицию, а также такие качества личности, как внимание, настойчивость, целеустремленность, инициативу, изобретательность, дисциплинированность, трудолюбие. Задачи на построения не просты. Не существует единого алгоритма для решения таких задач. Каждая из них по-своему уникальна, и каждая требует индивидуального подхода для решения. Инструменты, употребляемые для выполнения геометрических построений, весьма разнообразны. К основным инструментам принадлежат линейка и циркуль. Мы с вами уже встречались с задачами на построение. Мы строили угол заданной величины, треугольники по заданным сторонам, находили середину отрезка, зная его длину и т.д, при построении использовали линейку с и делениями и транспортир. Сегодня мы с вами рассмотрим задачи на построение с помощью циркуля и линейки без делений. Линейка считается без делений, даже если они на ней указаны. Решение задачи на построение состоит в том, что требуется построить с помощью циркуля и линейки без масштабных делений некоторую фигуру, если задана некоторая фигура или указаны некоторые соотношения между элементами искомой фигуры и элементами заданной фигуры. С помощью линейки можно провести произвольную прямую и прямую, проходящую через данные две точки. С помощью циркуля можно провести окружность с центром в данной точке и радиусом, равным данному отрезку. Решением задачи на построение называется фигура, удовлетворяющая условиям задачи. Найти решение задачи на построение – значит свести ее к конечному числу основных построений, после выполнения которых, искомая фигура будет уже считаться построенной. Решение задач на построение осуществляется в 4 этапа: Анализ (рисунок искомой фигуры, устанавливающий связи между данными задачи и искомыми элементами и план построения). Построение по намеченному плану. Доказательство, что данная фигура удовлетворяет условию задачи. Исследование (при любых ли данных задача имеет решение, и если имеет, то сколько). Для учащихся 7 класса – это первые шаги в изучении геометрии и построении фигур с помощью чертежных инструментов. В 7 классе мы с вами решаем самые простые задачи на построение, поэтому иногда достаточно только второго пункта алгоритма (или второго и третьего). Прежде чем приступить к решению задач на построение, я хочу напомнить вам, ребята, технику безопасности при работе с циркулем. Циркуль лежит с правой стороны, острием к себе. Без разрешения учителя его не берем. Передаем товарищам тупым концом. Чертим – упор на острие. Изучение нового материала. Основные задачи на построение: Построение отрезка, равного данному Построение прямой, проходящей через данную точку и перпендикулярную к данной прямой (точка не лежит на данной прямой) Построение прямой, проходящей через данную точку и перпендикулярную к данной прямой (точка лежит на данной прямой) Построение угла, равного данному. Построение биссектрисы угла Построение серединного перпендикуляра. Построение середины отрезка. Рассмотрим задачи на построение геометрических фигур с помощью циркуля и линейки, выполняя соответствующие построения и записи в тетрадях. Построение выполняем, используя презентацию. Задача №1 (слайд № 6 ) Построение отрезка, равного данному. Дано: луч ОА, отрезок МN Построить: ОВ = МN, В € ОА, Построение. 1. Окр.(О; МN); 2. Окр.(О; МN) ∩ ОА = В; 3. ОВ – искомый отрезок. Задача №2 (слайд № 7). Построение прямой, проходящей через данную точку и перпендикулярную к данной прямой (1 случай – точки не лежит на прямой Дано: прямая a, M ∉ a. Построить: b⊥a, M ∈ b. Построение: 1. Окр.(M;r), r – произвольный радиус 2. Окр.(M;r) ∩ a = A; А1. 3. Окр.(A;AM), Окр.(А1; А1 M). 4. Окр.(A;AM) ∩ Окр.(А1; А1 M) = K, M 5. MK = b – искомая прямая, b⊥a. Задача №3 (слайд № 8). Построение прямой, проходящей через данную точку, лежащую на прямой, и перпендикулярную к данной прямой. Дано: прямая a, O ∈ a Построить: b⊥a, O ∈ b, O ∈ a. Построение. 1. Окр.(O;r), r – произвольный радиус; 2. Окр.(O;r) ∩ a = A, B. 3. Окр.(A;AB), Окр.(B;AB). 4. Окр.(A;AB) ∩ Окр.(B;AB) = C. 5. OC⊥AB, OC=b, OC⊥a, b – искомая прямая. Устно доказываем, что полученная фигура удовлетворяет условию задачи на основе признака равенства треугольников. Физкультминктка. Гимнастика для глаз Задача №4 (слайд № 9 ). Построение угла, равного данному. Дано: BAC, OM – луч. Построить: B1OC1 = BAC. Построение. 1. Окр.(A;r), r – произвольный радиус. 2. Окр.(A;r) ∩ AB = B. 3. Окр.(A;r) ∩ AС = С. 4. Окр.(O;r) ∩ OM = C1. 5. Окр.(C1;BС) ∩ Окр.(O;r) = B1. 6. OB1, B1OC1 = BAC. B1OC1 – искомый. Равенство углов следует из равенства треугольников АВС и А1В1С1. Назовите признак равенства треугольников. Задача №5. (слайд № 10) Построение биссектрисы угла. Дано: ABC Построить: ВД – биссектриса ABC.\ Построение. Окр.(B;r), r – произвольный радиус. Окр.(B;r) ∩ AB = M. Окр.(B;r) ∩ BC = N. Окр.(M;r) ∩ Окр.(N;r) = D. 5. BD – искомая биссектриса ABC, ABD=CBD. Устно доказываем, что полученная фигура удовлетворяет условию задачи на основе признака равенства треугольников. Задача №6 (слайд № 11 ). Построение середины отрезка Дано: отрезок АВ. Построить: точку О – середину отрезка АВ. Построение. 1. Окр.(A;AB). 2. Окр.(B;BA). 3. Окр.(A;AB) ∩ Окр.(B;BA) = P, Q. 4. PQ – прямая. 5. PQ ∩ AB = O. 6. AO = BO, O – искомая точка. Устно доказываем, что полученная фигура удовлетворяет условию задачи на основе признака равенства треугольников. Ш. Закрепление изученного материала. Практическое задание. Работа выполняется по трем вариантам и имеет обучающий характер. Вариант №1. Разделить отрезок на 4 равные части. Вариант №2. Дан ∆АВС. Построить биссектрису ВК. Вариант №3. Дан ∆КМN. Построить медиану МР. IV . Итог урока Вопросы учащимся: Что нового вы сегодня узнали на уроке? Что научились делать? Предлагается обучающимся сделать выводы, какие построения можно выполнять, используя циркуль и линейку без масштабных делений. Учащиеся отвечают: с помощью циркуля и линейки можно построить угол, равный данному. биссектрису данного угла. отрезок, равный данному прямую, проходящую через данную точку и перпендикулярную к данной прямой (1 случай - точка не лежит на данной прямой, 2 случай - точка лежит на данной прямой) серединный перпендикуляр середину отрезка Обучающимся предлагается выполнить итоговый тест Угол АВС составляет 55о . Можно ли с помощью циркуля и линейки построить угол в 650? а) да б) нет 2. Какие инструменты используют при решении задач на построение? а) линейка без делений, циркуль б) угольник, транспортир в) масштабная линейка, циркуль 3. Как называется задача, в которой требуется построить фигуру с заданными свойствами с помощью чертежных инструментов? а) задача на строительство б) задача на построение в) задача на рисование Затем предлагается учащимся заполнить карточки, которые у них лежат на столах, оценить свою работу, выбрав один из вариантов ответа. Карточки учащимся для рефлексии: Фамилия имя_______________________________
Собрать карточки и тесты для оценки степени усвоения материала сегодняшнего урока, чтобы на следующем уроке правильно организовать работу. Учитель еще раз обращает внимание, на те теоретические факты, которые вспоминали на уроке, говорит о необходимости выучить их. V. Комментированное выставление оценок. Учитель отмечает наиболее успешную работу на уроке отдельных учащихся, при необходимости выставляет отметки. VI. Домашнее задание. В качестве домашнего задания учащиеся получают по варианту практической работы и обмениваются вариантами самостоятельной работы, проведенной на уроке. Учебник И.М.Смирнова, В.А.Смирнов. Геометрия, 7-9 классы, §20, с.87-89, изучить теорию, отвечать на вопросы №1-6, с.90-91,№7, с.91. Индивидуальное практическое домашнее задание . На столах у вас лежа карточки с двумя заданиями (вариант №1 и вариант №2), которые имеют два уровня сложности. На свое усмотрение выберите ту задачу, которую, по вашему мнению, вы сможете решить. Каждый шаг построения должен быть прокомментирован и обоснован Практическая работа учащегося 7 «а» класса Ф.И.______________________________________________ Вариант №1. Построить треугольник по данной стороне и данному углу. Дано: PQ – отрезок, hk 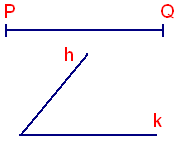 Построить: ∆ ABC, AB=PQ, ABC =hk, BAC = Построение. Самостоятельно описать построение и построить треугольник по данным элементам. Практическая работа учащегося 7 «а» класса Ф.И.______________________________________________ Вариант №2 Построить прямоугольный треугольник по двум сторонам. Дано: а – отрезок, в - отрезок Построить: ∆ ABC, С=90о, AС=а, СВ=b Построение. Самостоятельно описать построение и построить треугольник по данным элементам. |
