Ответы к экзамену по оптимизации бизнес процессов в системе gpss. Задачи оптимизации бп
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
Метод ЗейделяПусть результат решения описывается функцией полезности u=f(M)=f(x, x, . . . ,xn). Здесь через М обозначена точка n-мерного пространства решений со значениями управляемых переменных x, x, . . . ,xn: M=(x, x, . . . ,xn). Если целевая функция f(x, x, ... ,xn) задана явной формулой и является дифференцируемой, то мы можем вычислить ее частные производные и использовать их для определения направления убывания функции по каждой переменной и поиска соответствующих одномерных минимумов. Вопрос студентам: как найти экстремум функции? Зависимость 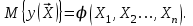 образует некоторую поверхность в (n + 1) – мерном пространстве образует некоторую поверхность в (n + 1) – мерном пространстве 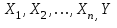 Эту поверхность принято называть поверхностью отклика, а отдельные её точки или значения y в точках 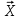 факторного пространства – просто «откликом». факторного пространства – просто «откликом».В тех случаях, когда зависимость 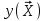 задана в аналитической форме, координаты задана в аналитической форме, координаты 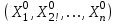 точки экстремума точки экстремума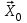 функции функции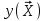 можно найти, решив систему уравнений вида: можно найти, решив систему уравнений вида: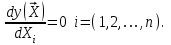 Решением системы (4) является так называемая «стационарная точка» 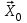 , в которой градиент функции , в которой градиент функции 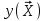 обращается в нуль обращается в нуль 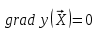 Напомним, что 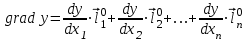 где 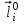 – единичный направляющий вектор координатной оси – единичный направляющий вектор координатной оси 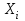 . .При принятии решений чаще всего явной формулы для целевой функции нет и задачу приходится решать эмпирическими методами. Для примера рассмотрим случай двух управляемых переменных х1 и х2. Изобразим поверхность отклика с помощью линий уровня. Вопрос студентам: что такое линия уровня? Пример топографических и морских карт. Вдоль этих линий функция сохраняет постоянные значения. На рис. изображены линии уровня некоторой функции двух переменных u= f (х, у). 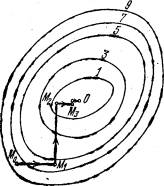 Рис. Пусть требуется найти минимум целевой функции (снизить затраты). Выберем какую-нибудь начальную точку М=(x, x, . . . ,xn0) и рассмотрим функцию f при фиксированных значениях всех переменных, кроме первой: f(x, x,x, . . . ,xn0 ). Тогда она превратится в функцию одной переменной x . Изменяя эту переменную, будем двигаться от начальной точки x=x в сторону убывания функции, пока не дойдем до ее минимума при x=x, после которого она начинает возрастать. Точку с координатами ( x, x,x, . . . ,xn0) обозначим через М, при этом f(M0) f(M). Фиксируем теперь переменные: x=x, x= x, . . . ,xn=xn0 и рассмотрим функцию f как функцию одной переменной x: f(x, x, x. . . ,xn0). Изменяя x , будем опять двигаться от начального значения x2=x20 в сторону убывания функции, пока не дойдем до минимума при x2=x21 .Точку с координатами {x, x, x . . . xn0} обозначим через М, при этом f(M1) f(M). Проведем такую же минимизацию целевой функции по переменным x, x, . . . ,xn. Дойдя до переменной xn, снова вернемся к x и продолжим процесс. Эта процедура вполне оправдывает название метода. С ее помощью мы построим последовательность точек М,М,М, . . . , которой соответствует монотонная последовательность значений функции f(M0) f (M)f(M) Обрывая ее на некотором шаге k можно приближенно принять значение функции f(Mk) за ее наименьшее значение в рассматриваемой области. Отметим, что данный метод сводит задачу поиска наименьшего значения функции нескольких переменных к многократному решению одномерных задач оптимизации. Условием прекращения вычислительной процедуры при достижении заданной точности может служить неравенство x(k+1) - x(k) < На рисунке показана траектория поиска наименьшего значения, которое достигается в точке О, с помощью метода покоординатного спуска. Градиентный методПри оптимизации процесса градиентным методом рабочее движение совершается в направлении наиболее быстрого возрастания или убывания выходного параметра, то есть в направлении градиента целевой функции 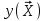 . Направление движения корректируется после каждого рабочего шага, то есть каждый раз заново вычисляется значение вектора . Направление движения корректируется после каждого рабочего шага, то есть каждый раз заново вычисляется значение вектора  grad grad 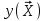 по результатам специально спланированных пробных экспериментов. по результатам специально спланированных пробных экспериментов.Поскольку координатами вектора градиента 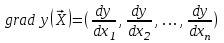 служат, как известно, коэффициенты при линейных членах разложения функции 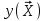 в ряд Тейлора по степеням в ряд Тейлора по степеням 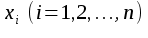 , то соответствующие компоненты вектора градиента могут быть получены как коэффициенты , то соответствующие компоненты вектора градиента могут быть получены как коэффициенты 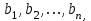 линейной аппроксимации поверхности отклика вблизи исходной точки линейной аппроксимации поверхности отклика вблизи исходной точки 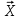 : : 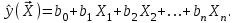 Для получения оценок линейных коэффициентов 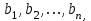 можно воспользоваться любым из известных способов экспериментального получения математической модели объекта. Например, можно реализовать для этой цели ПФЭ с центром в точке можно воспользоваться любым из известных способов экспериментального получения математической модели объекта. Например, можно реализовать для этой цели ПФЭ с центром в точке 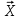 . Более простым хотя и менее точным, является способ определения каждого из коэффициентов . Более простым хотя и менее точным, является способ определения каждого из коэффициентов 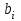 по результатам двух пробных движений из точки по результатам двух пробных движений из точки 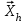 в точки в точки 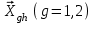 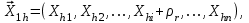 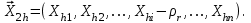 Тогда соответствующий коэффициент bi найдется по формуле 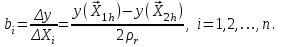 Процедура оптимизации методом градиента может быть выполнена по следующей схеме : 1) Задаётся шаг варьирования 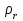 ,единый для всех независимых переменных ,единый для всех независимых переменных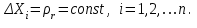 2) Задаётся параметр рабочего шага 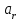 . .3) В начальной точке 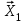 реализуется пробный эксперимент с целью определения направления для первого рабочего шага. Эксперимент проводится в соответствии с матрицей планирования ПФЕ. реализуется пробный эксперимент с целью определения направления для первого рабочего шага. Эксперимент проводится в соответствии с матрицей планирования ПФЕ.4) По результатам пробного эксперимента с помощью формулы (11) вычисляется вектор 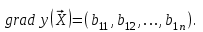 5) Совершается рабочий шаг в направлении grad 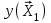 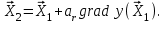 6) В точке 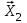 описанная выше процедура полностью повторяется. Очевидно, описанная выше процедура полностью повторяется. Очевидно, 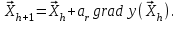 7) Поиск прекращается, когда модуль градиента y становится малой величенной 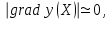 то есть все коэффициенты 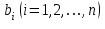 в уравнении (9) получаются незначимыми. в уравнении (9) получаются незначимыми.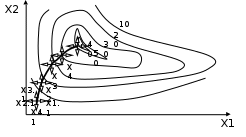 Характер движения к оптимуму при использовании градиентного метода иллюстрирует рис. Характер движения к оптимуму при использовании градиентного метода иллюстрирует рис. Симплексный методМетод предназначен для поиска локального экстремума и суть его заключается в следующем. В горизонтальной плоскости параметров 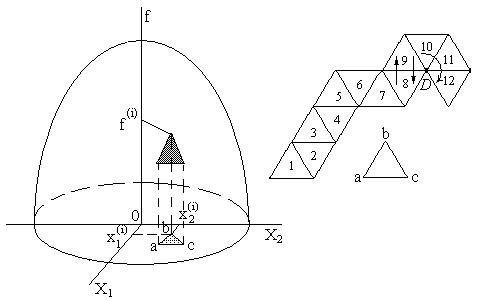 Рис. К обоснованию симплекс-метода для поиска экстремума Размер симплекса, определяемый длиной стороны, выбирается произвольно. Первоначальное его положение также не имеет принципиального значения. Главное условие – все его вершины должны проецироваться на поверхность отклика функции цели 1. Рассчитывают значения функционала во всех точках – проекциях вершин симплекса на поверхность отклика функции цели: 2. Производят количественное сравнение полученных значений функционала. 3. Если ищется максимальное значение функции цели, то из анализируемых значений выбирается наименьшее 4. На плоскости поворота предыдущего относительно той стороны треугольника, которая расположена против вершины, имеющей проекцию с минимальным значением функции цели. 5. Повторяют действия по п.п. 1-4 (перемещения симплекса на рис. показаны под номерами итерационных шагов) до тех пор, пока симплекс не начнет совершать периодические перемещения. Они могут быть двух типов: систематический поворот относительно одной из сторон (позиции 8-9, рис.), вращение вокруг какой-либо точки (например, точки D). 6. При появлении в поведении симплекса повторяемости в положениях следует уменьшить размер стороны симплекса и, взяв за базу одно из положений симплекса, продолжить вычисления. 7. Действия по п.п.1-6 повторяют до тех пор, пока размер стороны симплекса не достигнет заданной минимальной величины. 8. Определяют значение функции цели и оптимальный план по координатам той вершины симплекса в его окончательном положении, для которой значение функционала будет максимальным. Из описанного алгоритма метода видно, что для него характерен большой объем вычислительных операций. Поэтому реализация такого метода безусловно предпочтительно выполнять с привлечением вычислительной техники. При этом построение программного алгоритма и организация вычислений не могут вызвать больших затруднений. Тем не менее симплекс-метод может быть очень эффективен для многих приложений Ливеридж БПАнглийское слово leverage ['liːv(ə)rɪʤ] американцы читают "леверидж". В русскоязычной литературе встречается два названия ливеридж и леверидж. В прямом переводе "рычаг", поэтому часто этот показатель называется операционным рычагом. Определение Минимальный объем выручки, необходимый для покрытия всех расходов, называется точкой безубыточности. Точка безубыточности зависит от соотношения постоянных затрат, переменных затрат и цены продукции Запасом финансовой прочности называется величина, которая показывает на сколько может снизиться объем реализации, чтобы предприятие оказалось в точке безубыточности. Точка безубыточности большого магазина в сотни раз больше чем у продуктового ларька, но это не значит, что большой магазин финансово более устойчив. Это покажет только запас финансовой прочности. Он говорит о том насколько далеко предприятие от точки безубыточности. Маржинальная прибыль (marginal revenue, маржинальный доход) это разность дохода, полученного от реализации и переменных затрат. Она является источником покрытия постоянных затрат и источником образования прибыли. Формула расчета маржинальной прибыли: TRm = TR - TVC, где TRm — Маржинальная прибыль, TR — Доход (total revenue), TVC — Переменные затраты (total variable cost). Согласно другому определению – маржинальная прибыль это прирост общего объема прибыли, который предприятие получило от реализации дополнительной единицы товара. Кроме прочего, расчет маржинальной прибыли происходит на единицу товара, который производит и реализует то или другое предприятие, и дает показатель удельной маржинальной прибыли. Этот показатель нужен для того, чтобы показать динамику роста прибыли на каждую новую единицу продукции. |
