|
|
Ответы к экзамену по оптимизации бизнес процессов в системе gpss. Задачи оптимизации бп
Управляемые переменные в БП
Имитационное моделирование БП
Имитационная модель – это формальное описание логики функционирования исследуемой системы во времени, учитывающее наиболее существенные взаимодействия ее элементов и обеспечивающее возможность проведения статистических экспериментов. Имитационная модель СМО – это модель, отражающая поведение системы и изменения ее состояния во времени при заданных потоках требований, поступающих на входы системы. Параметры входных потоков требований – внешние параметры СМО.
Выходными параметрами являются величины, характеризующие свойства системы – качество ее функционирования, – например такие, как:
• коэффициенты использования каналов обслуживания;
• максимальная и средняя длина очередей в системе;
• время нахождения требований в очередях и каналах обслуживания и т.д.
Имитационное моделирование – это численный метод определения параметров функционирования самых различных систем по многочисленным реализациям с учетом вероятностного характера протекания процесса. Основой имитационного моделирования является метод статистических испытаний – метод МонтеКарло. Этот метод наиболее эффективен при исследовании сложных систем, на функционирование которых оказывают существенное влияние случайные факторы. Имитационное моделирование позволяет исследовать СМО при различных типах входных потоков и разной интенсивности поступления требований в систему, а также различных дисциплинах обслуживания требований. Модель в системе GPSSW – это последовательность операторов моделирования. Оператор моделирования может быть или оператором GPSS, или процедурой языка PLUS (Programming Language Under Simulation – Язык программирования для моделирования)
Пуассоновские случайные процессы
Итак, если количество испытаний 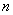 достаточно велико, а вероятность достаточно велико, а вероятность 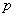 появления события появления события 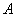 в отдельно взятом испытании весьма мала (0,05-0,1 и меньше), то вероятность того, что в данной серии испытаний событие в отдельно взятом испытании весьма мала (0,05-0,1 и меньше), то вероятность того, что в данной серии испытаний событие 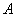 появится ровно появится ровно 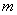 раз, можно приближенно вычислить по формуле Пуассона: раз, можно приближенно вычислить по формуле Пуассона:
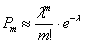 , где , где 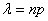
Напоминаю, что ноль факториал 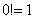 , а значит, формула имеет смысл и для , а значит, формула имеет смысл и для 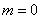 . .
Вместо «лямбды» также используют букву «а».
Характеристики:
События независимы друг от друга. Возникновение одного события не влияет на вероятность другого события.
Средняя скорость (события за период времени) постоянна. (т.е. среднее время одинаково с некоторыми отклонениями)
Два события не могут происходить одновременно.
вероятность
Распределение
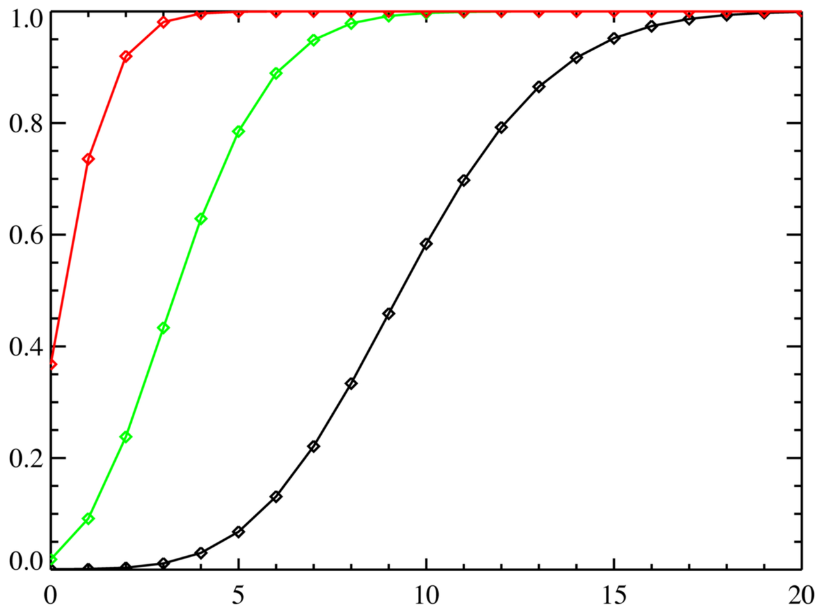
Экспоненциальное распределение времени
На рис. показан график функции плотности экспоненциального распределения.
Формула f(t) = λ * e^(−λt).
t – случайная величина, определяющая промежуток времени между событиями.
Экспоненциальное распределение позволяет предсказать следующее:
Время, по истечении которого клиент закончит поиск и закажет что-то в магазине (успех).
Время, по истечении которого конкретное оборудование выйдет из строя (отказ).
Время ожидания автобуса (прибытие).
У эксп. распределения только один параметр λ.
Важная вещь, которая позже поможет вам не запутаться с XEXP(0,25).0,25 — это не временной период, а число событий, совпадающее с параметром λ в процессе Пуассона.
Например, ваш блог посещают 500 пользователей в день. Это среднее значение. Количество клиентов магазина за час, землетрясений в год, автомобильных аварий в неделю, опечаток на странице и так далее — это средние значения событий (λ) в единицу времени, являющиеся параметром распределения Пуассона.
Однако при моделировании времени между событиями удобнее использовать термины времени, а не количества. Например, число лет, в течение которых компьютер может включаться без ошибок — 10 лет (это удобнее, чем говорить “0,1 ошибка в год”), новый покупатель приходит каждые 10 минут, крупные ураганы возникают каждые 7 лет и так далее.
Часто используется другой параметр µ - среднее число событий за период Т (каждые 10 минут, каждые 7 лет и т.д.) и является обратной величиной параметра (λ) в распределении Пуассона. Смотрите: если у вас 3 посетителя в час, значит у вас 1 посетитель каждую треть часа.
В течение единицы времени (неважно, в минутах, часах или годах) событие происходит в среднем 0,25 раз. Переводя в термины времени — пройдет в среднем 4 часа, прежде чем событие произойдет, если за единицу времени принят 1 час.
* Чтобы не запутаться: параметр экспоненциального распределения λ тот же самый, что в процессе Пуассона (λ).
Смотрите: в период ожидания не происходит ни одного события. Другими словами, Пуассон (X=0).
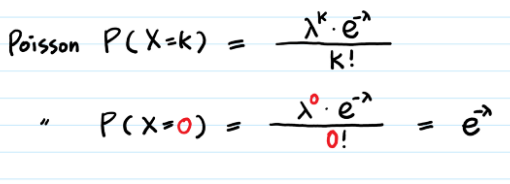
Пуассон (X=0): первый этап экспоненциального распределения
Есть важная вещь, которую стоит помнить о пуассоновской плотности вероятности: период времени, в течение которого возникают пуассоновские события (X=k), составляет только одну (1) единицу времени.
|
|
|
 Скачать 0.55 Mb.
Скачать 0.55 Mb.