Лекция № 8 – Моделирование систем массового обслуживания. Лекция 8 Моделирование систем массового обслуживания. При исследовании многих реальных сложных систем возникает не

• Название: Лекция 8 Моделирование систем массового обслуживания. При исследовании многих реальных сложных систем возникает не
• Анкор: Лекция № 8 – Моделирование систем массового обслуживания.
• Дата: 18.10.2021
• Размер: 35.52 Kb.
• Имя файла: 8.docx
• Тип: Лекция; #250177

Лекция № 8 – Моделирование систем массового обслуживания.

При исследовании многих реальных сложных систем возникает не­обходимость в решении задач, относящихся к массовому обслуживанию. Однако аналитический аппарат теории массового обслуживания позволя­ет решить далеко не все задачи, представляющие практический интерес, и ограничивается, в основном, задачами, в которых входные потоки ап­проксимируются простейшим потоком, а время обслуживания предпола­гается распределенным но показательному закону. В связи с этим для ис­следования сложных систем, приводимых к схеме систем массового об­служивания (СМО). целесообразно использовать компьютерное модели­рование.

Сущность этого метода применительно к анализу систем массового обслуживания заключается в следующем. С помощью изложенных ранее методов моделирования случайных закономерностей формируются реали­зации заданного потока заявок. Далее моделируется процесс функциони­рования обслуживающей системы. Все показатели работы системы, инте­ресующие исследователя, фиксируются. Общий моделирующий алгоритм многократно воспроизводит случайные реализации процесса функциони­рования системы при некоторых заранее заданных условиях. Накопленная при этом информация статистически обрабатывается.

Постановка задачи. Мы изучим здесь классическую задачу теории массового обслуживания в тех условиях, в каких она была рассмотрена и решена Эрлангом. На m одинаковых приборов поступает простейший поток требований интенсивности . Если в момент поступления требования имеется хотя бы один свободный прибор, оно немедленно начинает обслуживаться. Если же все приборы заняты, то вновь поступившее требование становится в очередь за всеми теми требованиями, которые поступили раньше и еще не начали обслуживаться. Освободившийся прибор немедленно приступает к обслуживания очередного требования, если только имеется очередь. Каждое требование обслуживается только одним прибором, и каждый прибор обслуживает в каждый момент не более одного требования. Длительность обслуживания представляет собой случайную величину с одним и тем же распределением вероятностей F(x).

Система с ожиданием в случае простейшего потока и показательного времени обслуживания представляют собой случайный процесс Маркова.

Найдём те уравнения, которым удовлетворяют вероятности P_k(t). Одно из уравнений очевидно, а именно для каждого t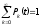

. (2)

Найдем сначала вероятность того, что в момент t+h все приборы свободны. Это может произойти следующими способами:

в момент t все приборы были свободны и за время h новых требований не поступало;

в момент t один прибор был занят обслуживанием требования, все остальные приборы свободны; за время h обслуживание требования было завершено и новых требований не поступило.

Остальные возможности, как-то: были заняты два или три прибора и за время h работа на них была закончена - имеют вероятность o(h), как легко в этом убедится.

Вероятность первого из указанных событий равна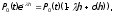



вероятность второго события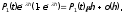



Таким образом,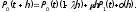



Отсюда очевидным образом приходим к уравнению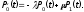

(3)

Перейдем теперь к составлению уравнений для P_k(t) при k  1. Рассмотрим отдельно два различных случая: 1  k  m и k  m. Пусть вначале 1  k  m. Перечислим только существенные состояния, из которых можно прийти в состояние E_k в момент t+h. Эти состояния таковы:

В момент t система находилась в состоянии E_k, за время h новых требований не поступило и ни один прибор не окончил обслуживания. Вероятность этого события равна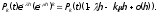



В момент t система находилась в состоянии E_k-1, за время h поступило новое требование, но ни одно ранее находившееся требование не было закончено обслуживанием. Вероятность этого события равна



В момент t система находилась в состоянии E_k+1 , за время h новых требований не поступило, но одно требование было обслужено. Вероятность этого равна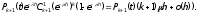



Все остальные мыслимые возможности перехода в состояние E_k за промежуток времени h имеют вероятность, равную 0(h).

Собрав воедино найденные вероятности, получаем следующее равенство: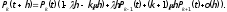



Несложные преобразования приводят нас к такому уравнению для 1  k  m: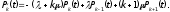

(4)

Подобные же рассуждения для k  m приводят к уравнению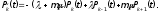

` (5)

Для определения вероятностей P_k(t) мы получили бесконечную систему дифференциальных уравнений (2)-(5). Ее решение представляет несомненные технические трудности.